Добавлен: 28.11.2018
Просмотров: 3564
Скачиваний: 53

6
Таблица 1.2
Номер ИМ
1
2
3
4
5
6
[мм] при t = 0 ч
0,2
0,15
0,18
0,14
0,1
0,16
[мм] при t = 50 + 12·N ч
0,25
0,18
0,21
0,19
0,15
0,22
Для использования ИМ в задвижках нефтепровода необходимо,
чтобы погрешность его позиционирования была
0,2
мм.
Полагая, что скорость изменения погрешности подчиняется нор-
мальному закону распределения, определите интервал проведения про-
филактических работ для ИМ данного типа, исключающий их посте-
пенные отказы с вероятностью
.
9
,
0
P
12. Рассчитать время проведения профилактического ремонта си-
стемы управления, имеющей значение главного параметра
5
4
0
,
X
, до-
пуск на параметр (
0,5), среднеквадратичное отклонение
0
σ
0,2
, если
известно, что
0
0
0,1 , σ
σ
0,03
m t
m
t
t
t
, а в момент начала прове-
дения профилактических работ требуемая вероятность
98
,
0
)
(
проф
t
P
.
13. Устройство состоит из четырёх групп элементов, в каждой из ко-
торых, соответственно, N
1
= 35, N
2
= 14, N
3
= 18, N
4
= 26 элементов с ин-
тенсивностями отказов
4
1
λ
5 10
ч
–1
,
4
2
λ
1,8 10
ч
–1
,
4
3
λ
8 10
ч
–1
,
4
4
λ
1 10
ч
–1
.
Элементы 2 и 3 групп восстанавливаемы со временем восстановле-
ния
2
τ
20
B
ч,
3
τ
30
B
ч. Пополнение элементов 1 и 4 групп в ЗИПе
проводится через 500 часов.
Определите, сколько элементов каждой группы должно быть
в ЗИПе, чтобы его достаточность была не менее 0,9?

7
Вариант 2
Тема 1. Расчет надёжности систем
1. Система имеет нормальное распределение наработки до отказа
с параметрами
1200 ч,
750 ч
t
t
m
. Область возможных значений
наработки до отказа (0,
). В течение какой наработки (0, t) система бу-
дет функционировать с вероятностью безотказной работы не менее, чем
0,95.
2. Оцените вероятность безотказной работы в течение времени
t = 15 000 часов изнашиваемого подвижного соединения, если ресурс по
износу подчиняется нормальному распределению с параметрами
40 000 ч,
10 000 ч.
t
t
m
3. По результатам испытания 300 приводов исполнительных меха-
низмов, проводившихся без замен и отказавших в течение 1 000 часов,
были получены данные о наработках до отказа, приведённые в табл. 2.1.
Таблица 2.1
Интервалы наработки
, ч
i
t
0–100 100–200 200–400 400–600 600–800 800–1000
Число отказов
i
n t
60
80
70
45
20
25
Вычислить значения и построить графики вероятности безотказной
работы, интенсивности отказов, частоты отказов приводов исполни-
тельных механизмов.
4. На насосной станции магистрального трубопровода установле-
ны 3 насоса, наработка до отказа которых определяется нормальным за-
коном распределения с параметрами:
насос 1: m
1
= 2500 ч, σ
1
= 1400 ч;
насос 2: m
2
= 3000 ч, σ
2
= 1100 ч;
насос 3: m
3
= 4000 ч, σ
3
= 1400 ч.
Время безотказной работы системы управления насосами опреде-
ляется законом Рэлея с параметром λ
С
= 0,0003 ч
–1
. Определите, какова
будет вероятность безотказной работы манипулятора через неделю
непрерывной работы в три смены?
5. Установлено, что наработка до отказа привода задвижки имеет
распределение Вейбулла с параметром
1,5
. Вероятность безотказной
работы привода в течение наработки (0, 200) часов равна 0,90. Требует-
ся определить интенсивность отказов в момент времени t = 200 ч,
и среднюю наработку до отказа привода.
8
Тема 2. Обеспечение заданного уровня надёжности технических
систем
6. Структурная схема надёжности системы имеет вид «сложного
мостика», показанного на рис. (2.1)
Рис. 2.1. Структурная схема надёжности системы
Для элементов 1, 5:
4
1
,
2 10
ч ,
0,7;
t
P t
e
3, 6:
2
4
1
,
3 10
ч
t
P t
e
.
Элемент 4 имеет нормальное распределение времени безотказной
работы с параметрами
1500 ч,
300 ч;
t
t
m
элементы 2 и 7 имеют
экспоненциальное распределение с интенсивностью
4
1
2
2,5 10 ч ,
5
1
7
9 10
ч .
Определите вероятность безотказной работы системы в момент
времени t = 2000 часов.
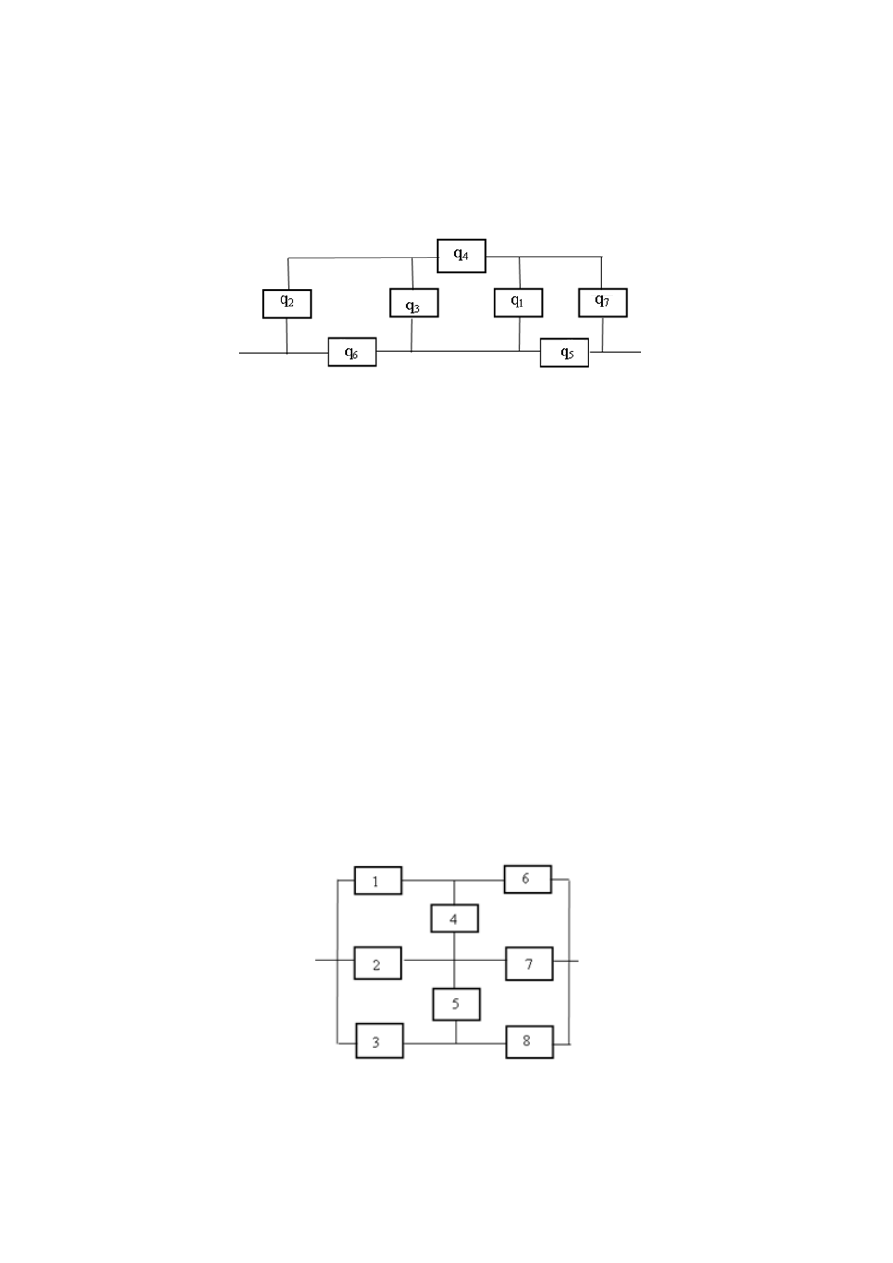
7. Найти вероятность безотказной работы за время наработки
в 200 часов системы, имеющей структурную схему надежности
(рис. 2.2), если для звеньев 1, 2, 3, 4, 5, 6
95
,
0
P
. Для звена 7 веро-
ятность безотказной работы определяется по закону Вейбулла с пара-
метрами
0,4
;
1
0,001 ч ;
для звена 8 – по закону Рэлея с пара-
метром
3
1
2 10
ч
.
Рис. 2.2. Структурная схема надёжности системы

9
Тема 3. Основные вопросы эксплуатационной надёжности тех-
нических систем
8. В системе телеуправления применено дублирование канала
управления. Интенсивность отказов канала
2
1
10 ч
. Рассчитать веро-
ятность безотказной работы системы P
S
(t), при t = 10 ч, среднее время
безотказной работы системы T
S
, частоту отказов a
S
(t) и интенсивность
отказов
( )
S
t
.
9. Система состоит из 5 равнонадежных элементов, вредняя
наработка до первого отказа элемента равна 2000 час. Предполагается,
что для элементов системы справедлив экспоненциальный закон
надежности и основная и резервная системы равнонадежны. Найти
вероятность безотказной работы и среднюю наработку до первого
отказа системы в следующих случаях: а) нерезервированной системы;
б) дублированной системы при постоянно включенном резерве;
в) дублированной системы при включении резерва по способу
замещения; г) дублированной системы при включении ненагруженного
раздельного резерва по способу замещения.
10. Интенсивность отказов λ
c
восстанавливаемой системы подза-
рядки аккумулятора λ
c
= 0,015 1/час = const. Среднее время воcстанов-
ления t
в
= 100 час. Какова вероятность застать систему в исправном со-
стоянии в момент времени t = 10 час.
Тема 4. Диагностика автоматизированных систем
11. При испытаниях партии исполнительных механизмов (ИМ) из
6 штук было установлено, что погрешность позиционирования со време-
нем увеличивается. Данные о погрешностях, полученные для моментов
времени эксплуатации t
1
= 0 ч, t
2
= 40 + 10·N ч приведены в табл. 2.2.
Таблица 2.2
Номер ИМ
1
2
3
4
5
6
[мм] при t = 0 ч
0,18
0,13
0,16
0,12
0,08
0,14
[мм] при t = 40 + 10·N ч
0,22
0,15
0,18
0,16
0,12
0,19
Для использования ИМ в задвижках нефтепровода необходимо,
чтобы погрешность его позиционирования была ∆ ≤ 0,15 мм.
Полагая, что скорость изменения погрешности подчиняется нор-
мальному закону распределения, определите интервал проведения про-
филактических работ для ИМ данного типа, исключающий их посте-
пенные отказы с вероятностью
.
92
,
0
P

10
12. Рассчитать время проведения профилактического ремонта си-
стемы управления, имеющей значение главного параметра
5
,
5
0
X
, до-
пуск на параметр (
0,4), среднеквадратичное отклонение
18
,
0
σ
0
, ес-
ли известно, что
t
t
t
m
t
m
04
,
0
σ
)
(
σ
,
2
,
0
)
(
0
0
, а в момент начала
проведения
профилактических
работ
требуемая
вероятность
97
,
0
)
(
проф
t
P
.
13. Устройство состоит из четырёх групп элементов, в каждой из ко-
торых, соответственно, N
1
= 38, N
2
= 12, N
3
= 20, N
4
= 23 элементов интен-
сивностями отказов
4
1
10
4
λ
ч
–1
,
4
2
10
5
,
1
λ
ч
–1
,
4
3
10
7
λ
ч
–1
,
4
4
10
5
,
1
λ
ч
–1
.
Элементы 2 и 3 групп восстанавливаемы со временем восстановле-
ния
23
τ
2
В
ч,
35
τ
3
В
ч. Пополнение элементов 1 и 4 групп в ЗИПе
проводится через 600 часов.
Определите, сколько элементов каждой группы должно быть
в ЗИПе, чтобы его достаточность была не менее 0,85?