Добавлен: 28.11.2018
Просмотров: 3566
Скачиваний: 53
41
Тема 3. Основные вопросы эксплуатационной надёжности тех-
нических систем
8. Устройство состоит из трех блоков I, II, III. Интенсивности отказов
этих трех блоков соответственно равны
6
1
18 10
1/ч,
6
2
25 10
1/ч,
6
3
12 10
1/ч. Требуется определить вероятность безотказной работы
устройства P
C
(t) для следующих случаев: а) резерв отсутствует, б) име-
ется дублирование устройства в целом.
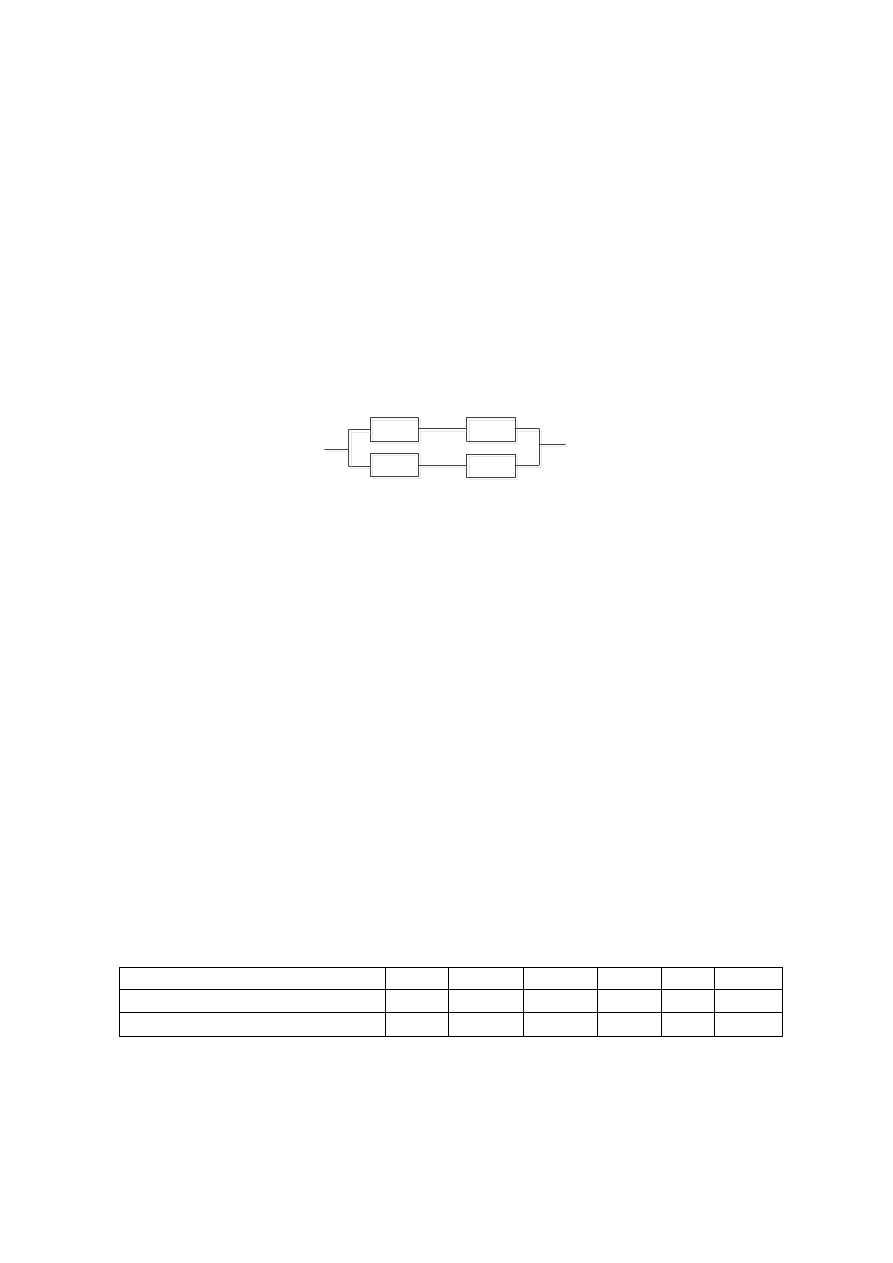
9. Схема расчета надежности изделия приведена на рис. 10.3. Найти
вероятность безотказной работы изделия, если известны вероятности
безотказной работы элементов: P
1
= 0,9; P
2
= 0,8; P
3
= 0,85; P
4
= 0,94.
P
1
P
2
P
3
P
4
Рис. 10.3. Схема расчета надежности изделия
10. Вероятность безотказной работы преобразователя постоянного
тока в переменный в течении времени t = 1000 ч равна 0,95, т.е.
P(1000) = 0,95. Для повышения надежности системы электроснабжения
на объекте имеется такой же преобразователь, который включается
в работу при отказе первого (режим ненагруженного резерва). Требует-
ся рассчитать вероятность безотказной работы P
C
(t) и среднее время
безотказной работы системы T
0
, состоящей из двух преобразователей,
а также определить частоту отказов a(t) и интенсивность отказов λ(t) си-
стемы.
Тема 4. Диагностика автоматизированных систем
11. При испытаниях партии исполнительных механизмов (ИМ) из
6 штук было установлено, что погрешность позиционирования со време-
нем увеличивается. Данные о погрешностях, полученные для моментов
времени эксплуатации t
1
= 0 ч, t
2
= 45 + 14·N ч приведены в табл. 10.2.
Таблица 10.2
Номер ИМ
1
2
3
4
5
6
[мм] при t = 0 ч
0,21
0,16
0,19
0,15
0,11
0,17
[мм] при t = 45 + 14·N ч
0,26
0,19
0,22
0,20
0,16
0,23
Для использования ИМ в задвижках нефтепровода необходимо,
чтобы погрешность его позиционирования была ∆ ≤ 0,23 мм.

42
Полагая, что скорость изменения погрешности подчиняется нор-
мальному закону распределения, определите интервал проведения про-
филактических работ для ИМ данного типа, исключающий их посте-
пенные отказы с вероятностью
.
9
,
0
P
12. Рассчитать время проведения профилактического ремонта систе-
мы управления, имеющей значение главного параметра
5
,
2
0
X
, допуск
на параметр (
0,45), среднеквадратичное отклонение
12
,
0
σ
0
, если из-
вестно, что
t
t
t
m
t
m
09
,
0
σ
)
(
σ
,
15
,
0
)
(
0
0
, а в момент начала проведе-
ния профилактических работ требуемая вероятность
91
,
0
)
(
проф
t
P
.
13. Устройство состоит из четырёх групп элементов, в каждой из ко-
торых, соответственно, N
1
= 36, N
2
= 16, N
3
= 23, N
4
= 14 элементов с интен-
сивностями отказов
4
1
10
5
,
8
λ
ч
–1
,
4
2
10
5
,
3
λ
ч
–1
,
4
3
10
5
,
7
λ
ч
–1
,
4
4
10
5
,
2
λ
ч
–1
.
Элементы 2 и 3 групп восстанавливаемы со временем восстановле-
ния
30
τ
2
В
ч,
20
τ
3
В
ч. Пополнение элементов 1 и 4 групп в ЗИПе
проводится через 600 часов.
Определите, сколько элементов каждой группы должно быть
в ЗИПе, чтобы его достаточность была не менее 0,95?