ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5662
Скачиваний: 10
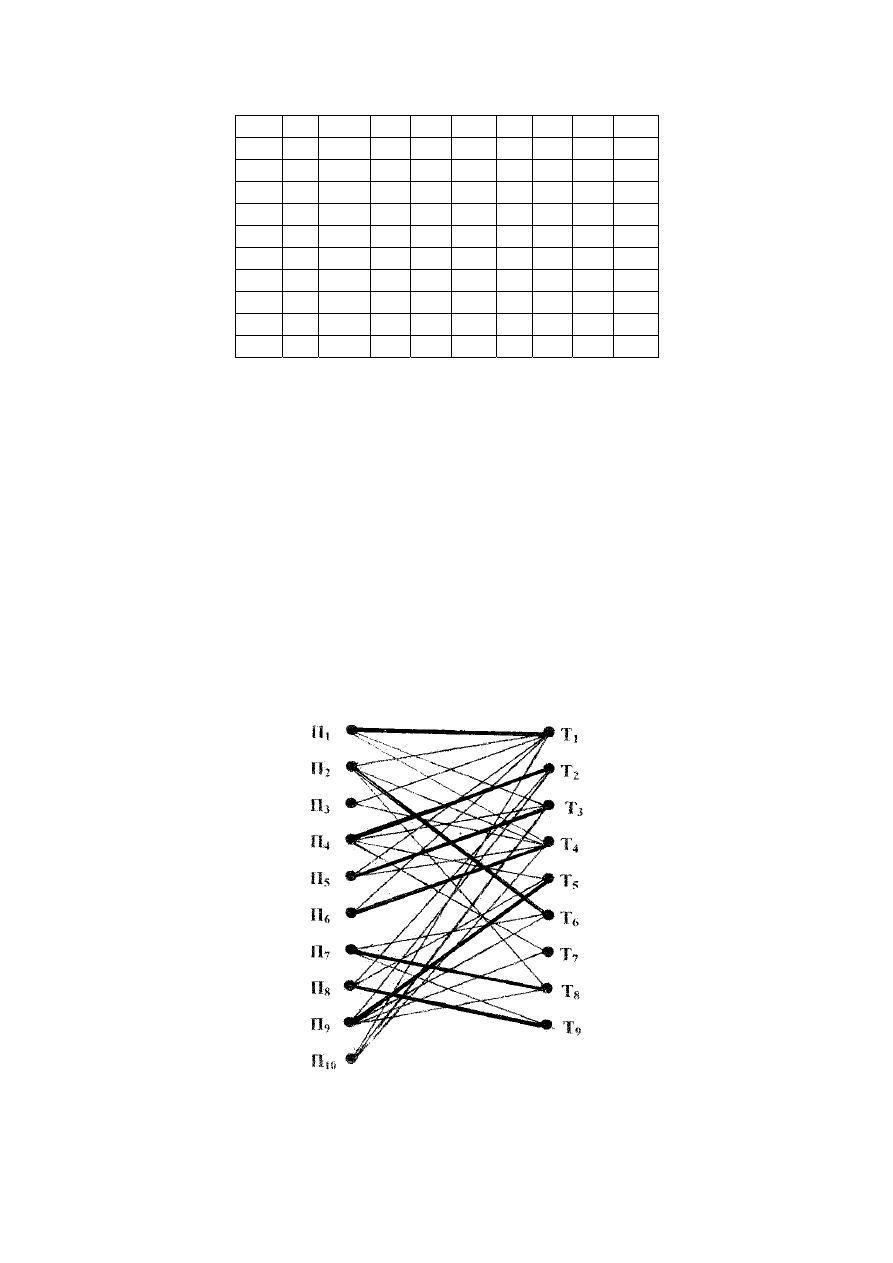
51
Рисунок 2.4.4
Из матрицы B (рисунок 2.4.4) видно, что увеличить тонкую
чередующуюся цепь Q нельзя, но в графе остались ненасыщен-
ные вершины, инцидентные одному и тому же рёбру, которые
можно добавить к к искомому паросочетанию K
ν
. Это рёбра П
8
,
Т
9
; П
4
, Т
2
.
В результате получаем наибольшее
паросочетание
K
ν
(рисунок 2.4.5), в которое входят рёбра: (П
5
,Т
3
),(П
1
,Т
1
),(П
6
,Т
4
),
(П
2
,Т
6
), (П
7
,Т
8
), (П
9
,Т
5
), (П
8
, Т
9
), (П
4
, Т
2
)
.
На рисунке 2.4.5 рёбра
поросочетания обозначены жирными линиями.
Рисунок 2.4.5
Т1 Т2
Т3 Т4 Т5* Т6 Т7 Т8 Т9
П1 1+ 1–
1
П2 1
1–
1+ 1
П3
1
1
П4
1 1 1 1
П5* 1
1+ 1
П6
1–
1+
П7
1–
1+
1
П8
1 1 1
П9
1 1+
1
1
1–
П10 1
1
52
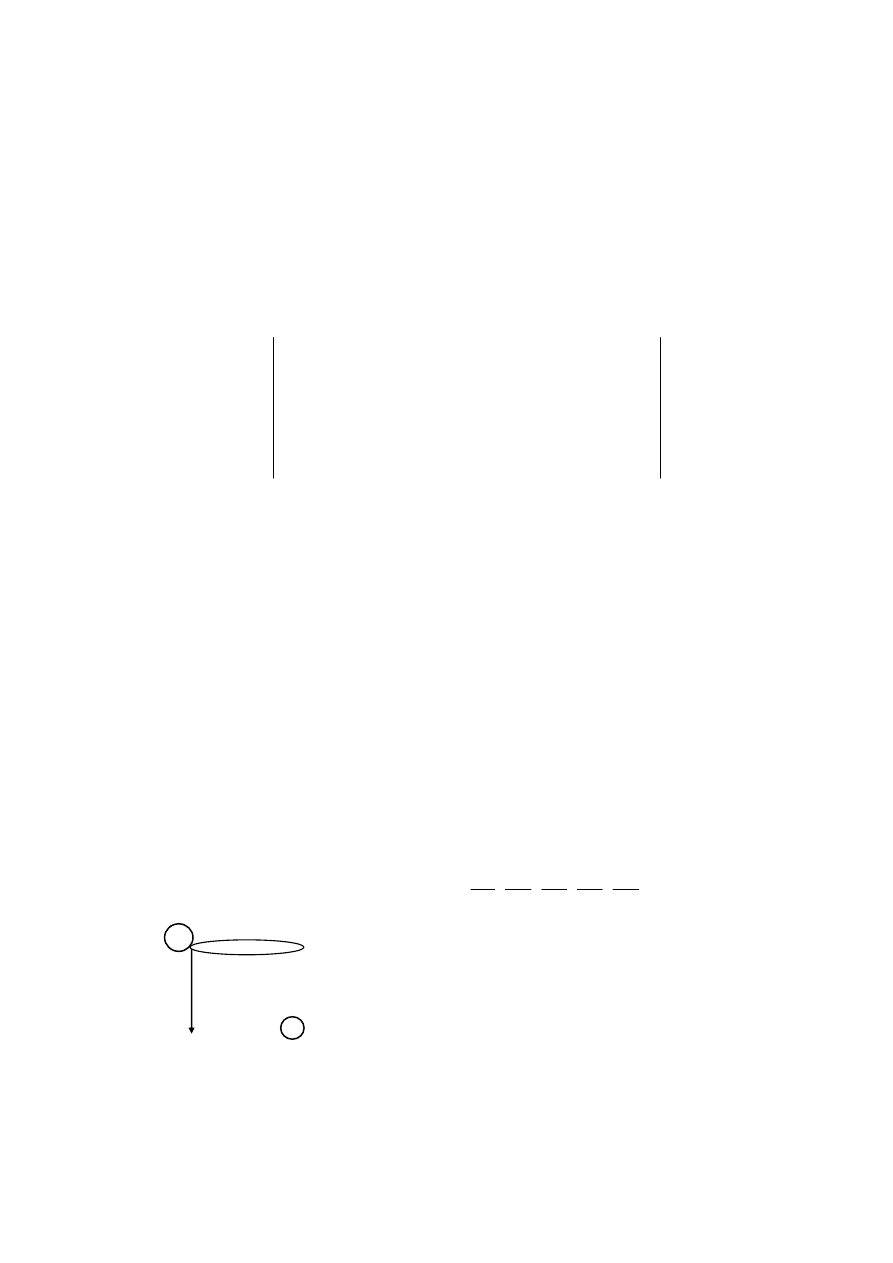
Графы Бержа
1-орграф L=(x,u,p), называется графом Бержа; он характе-
ризуется тем, что у него нет звеньев, и из одной вершины в дру-
гую может идти не более одной дуги и при вершине может быть
не более одной петли.
Наложение на полукольцо К соотношений
ηξ=0, ξη=ζ
2
=1
приводит к следующему выражению для матрицы смежности
графа Бержа:
)
(
...
)
,
(
)
,
(
....
..........
...
..
..........
.
..........
)
,
(
...
)
(
)
,
(
)
,
(
...
)
,
(
)
(
0
2
1
2
2
0
1
2
1
2
1
1
0
n
n
n
n
n
x
S
x
x
S
x
x
S
x
x
S
x
S
x
x
S
x
x
S
x
x
S
x
S
R
+
+
+
+
+
+
=
где
( )
(
)
⎩
⎨
⎧
−
∃
−
=
случае.
противном
в
0
истинно;
если
1
0
иx
x
р
u
x
S
i
i
i
( )
( )
( )
⎩
⎨
⎧
−
∃
−
=
=
−
+
случае.
противном
в
0
истинно;
если
1
j
i
j
i
j
i
x
x
p
u
x
x
S
x
x
S
Граф Бержа определяется однозначно с точностью до инди-
видуализации ребер заданием на Х бинарного отношения
J (x,y)=
∃ и P(x,y.u).
Вместо отношения
r
J
обычно задают отображение Г, отно-
сящее каждой вершине х
∈Х подмножество
Гх={y
⎪y∈x& J (x,y)}.
Поэтому граф Бержа можно обозначать через (Х,Г), а также
через (X,U). Например, для графа, представленного на рисунке,
X={1,2,3,4},
}
44
,
32
,
23
,
22
,
21
{
=
U
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
=
1
0
0
0
0
0
1
0
0
1
1
1
0
0
0
0
R
2
1
53
2.5
Части
с
экстремальными
свойствами
в
графах
Подграф L
/
графа L называется максимальным полным
(пустым)
подграфом, если он полный (пустой) и не существует
такого подграфа, который содержал бы L
/
, не совпадая с ним, и
тоже был бы полным (пустым).
Подграф L
/
называется наибольшим полным (пустым) под-
графом, если среди всех полных (пустых) подграфов он содержит
наибольшее число вершин.
Число
ε(L), характеризующее число вершин наибольшего
пустого подграфа, называется неплотностью графа.
Число
ϕ(L), характеризующее число вершин наибольшего
полного подграфа, называется плотностью графа.
В иной терминологии
ε(L) называется числом внутренней
устойчивости.
Дополнительным графом для обыкновенного графа L на-
зывается обыкновенный граф
)
,
(
U
X
L
=
с тем же множеством
вершин и новым множеством ребер
.
\
}
&
,
/
{
~
U
y
x
X
y
x
xy
U
≠
∈
=
Иначе говоря, такой граф, в котором две различные верши-
ны смежны тогда и только тогда, когда они не смежны в исход-
ном графе.
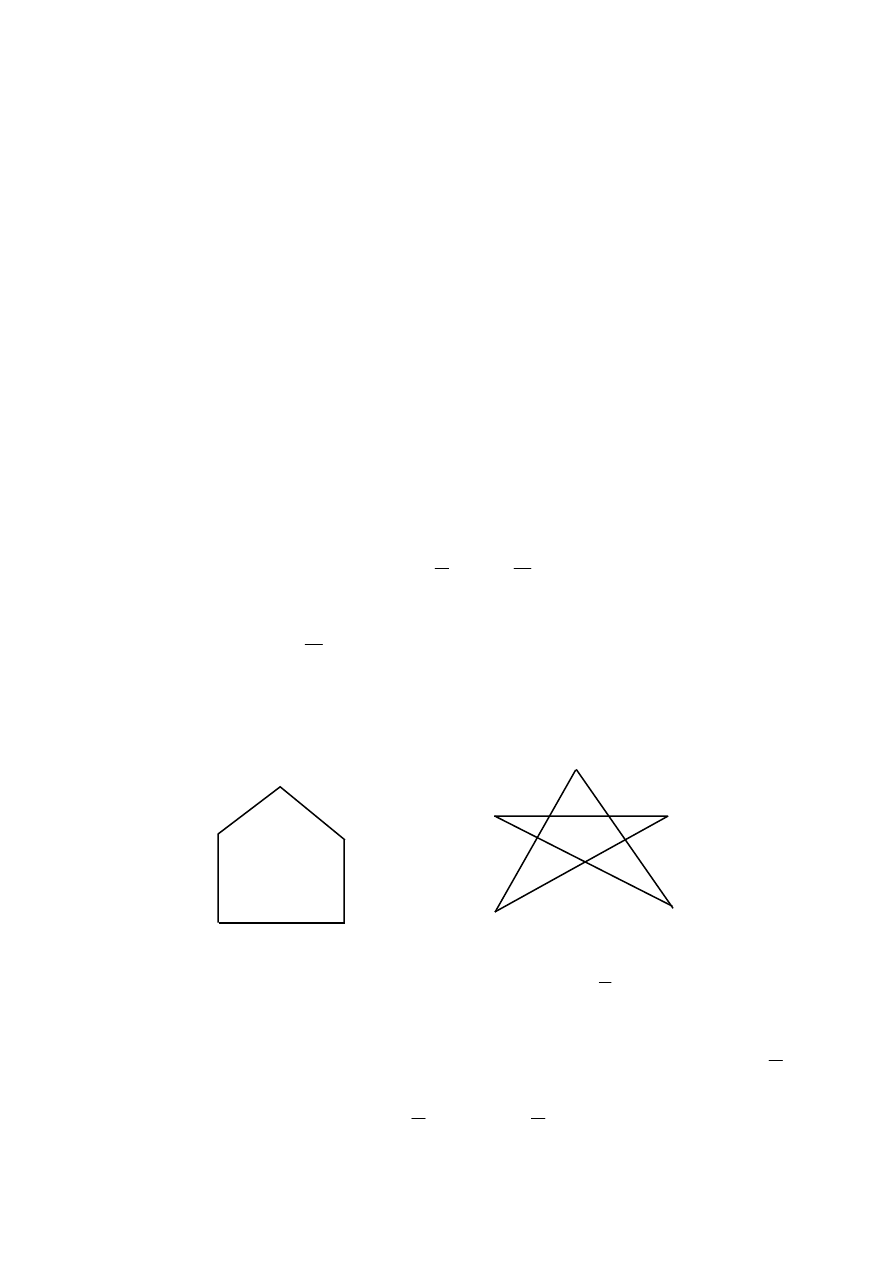
3 3
2 4 2 4
1 5 1 5
L L
Рисунок 2.5
Для графа L (рисунок 2.5, а) и его дополнительного графа
L
(рисунок 2.5, б) очевидно, что
ϕ(L)=ε(
L
);
ε(L)=ϕ(
L
).
а)
б)

54
В иной терминологии максимальный полный подграф назы-
вается
кликой. Рассмотрим ряд примеров.
Пример 2.5.1. Задача о восьми ферзях.
Можно ли на шахматной доске разместить восемь ферзей
так, чтобы ни один из них не находился под ударом какого-либо
другого.
Эта задача сводится к нахождению наибольшего пустого
подграфа в графе с 64 вершинами (клетки шахматной доски), где
клетки х и у смежны, если находятся в одной и той же горизонта-
ли, вертикали или диагонали. Эта задача имеет 92 решения.
Пример 2.5.2. Пусть Х
− множество лиц, а смежность вер-
шины х и у означает согласие между соответствующими лицами.
Требуется найти общество с наибольшим числом взаимно соглас-
ных членов, т.е. «максимальную клику».
Пример 2.5.3. Задача об информационной емкости множест-
ва сигналов.
Рассматривается простейший случай одного передатчика,
который может передавать четыре сигнала х
1
, х
2
, х
3
, х
4
; при прие-
ме каждый из этих сигналов может быть истолкован неоднознач-
но: сигнал х
1
дает у
1
или у
3
, сигнал х
2
дает у
1
или
у
2
и т.д. (рису-
нок 2.5.1.а)
x1 y1 x1 x2
x2 y2
x3 y3
x4 y4
а) б)
Рис. 2.5.1
x3
x4
55
Какое наибольшее число сигналов можно принять, не рис-
куя спутать их друг с другом? Задача сводится к определению
наибольшего пустого подграфа L (рисунок 2.5.1, б), где две вер-
шины смежны, если соответствующие системы можно спутать
при приеме.
Примером части с экстремальными свойствами является его
опора.
Опорой
графа L=(X,U;P) называется такой его подграф
L’=(X’,U’,P’), что всякое ребро u
∈U инцидентно по крайней мере
одной вершине из Х’.
Количество
σ(L) вершин наименьшей опоры называется
опорным числом графа L.
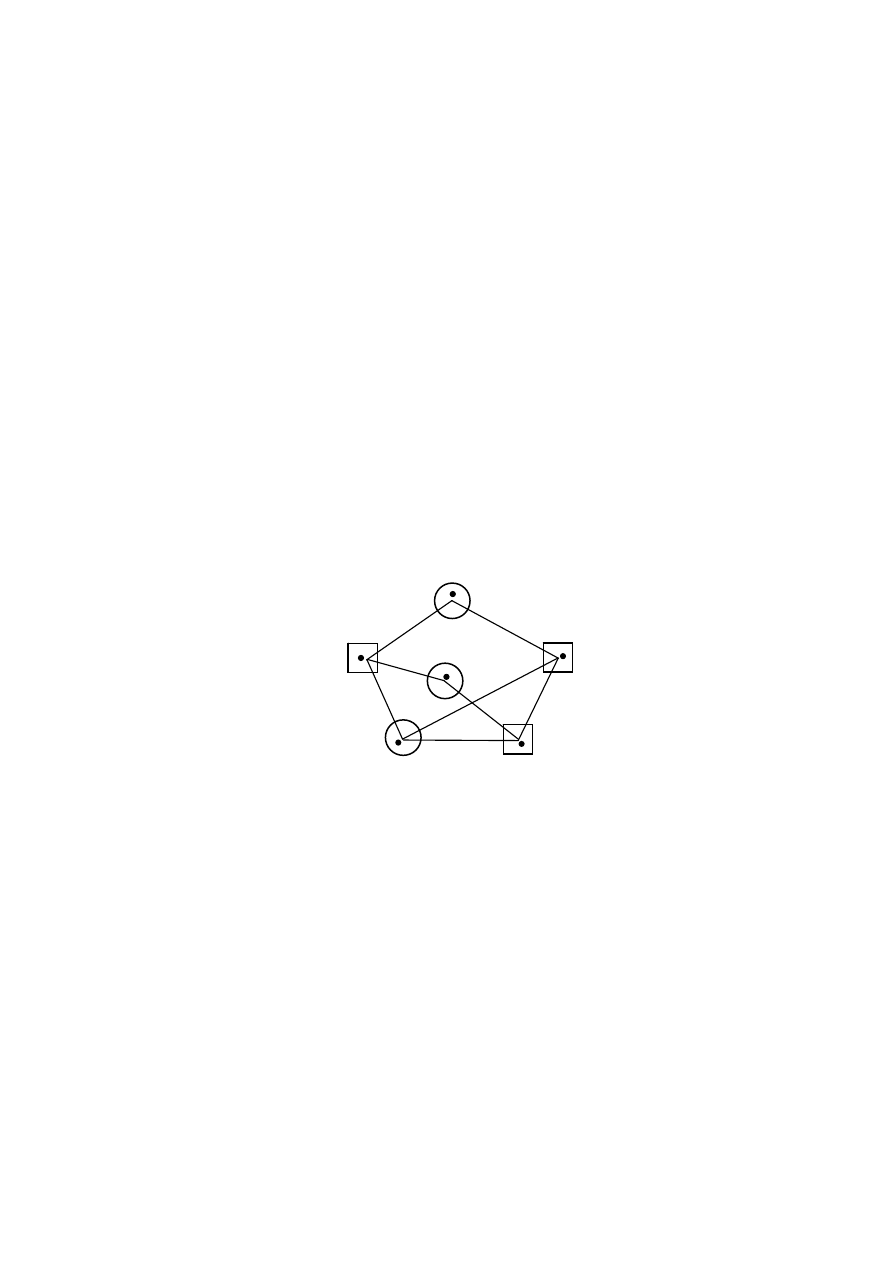
Пример 2.5.4. Задача о часовых. В тюрьме около каждой ка-
меры может быть поставлен часовой. Как, используя наименьшее
число часовых, обеспечить просматриваемость всех коридоров.
Рис. 2.5.2
Ясно, что подграф L’ есть опора графа L тогда и только то-
гда, когда подграф L’’, порожденный множеством Х\Х’ осталь-
ных вершин, пуст, и что опора L’ минимальна в том и только в
том случае, если соответствующий пустой подграф L’’ максима-
лен (в частности наименьшей опоре отвечает наибольший пустой
подграф). Отсюда следует, что задачи выявления максимальных
пустых подграфов и минимальных опор равносильны и что
ε(L) +σ(L)=n(L). Для примера (рисунок 2.5.2) вершины множества
Х’ обведены кружком, а вершины, образующие опору, – квадра-
том.
Наименьший всесмежный подграф, или наименьший
внешне неустойчивый подграф
L’=(x’,u’,p’), который обладает