ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5661
Скачиваний: 10
61
добавить соотношение: 2=1, тем самым преобразуя полукольцо в
булеву алгебру B{0,1}.
Элемент матрицы r
(l)
ij
будет тогда равен единице, если суще-
ствует хотя бы один маршрут длины l из i-ой вершины в j-ю, и
нулю в противном случае.
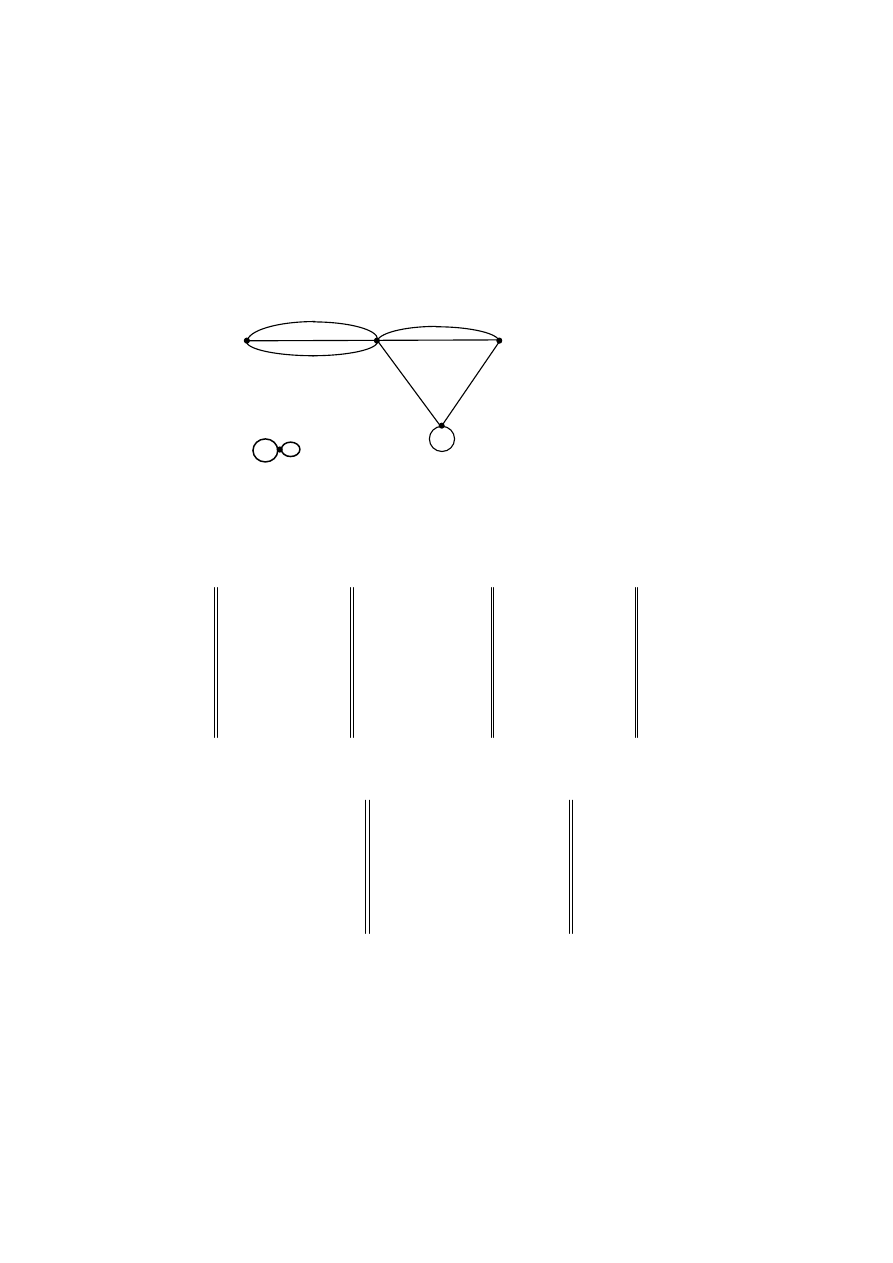
Рассмотрим следующий пример
1 b 4
а 2 5 c
3
8 6
9 10 7
Рис. 3.1.1
a b c d e a b c d e
2
0
0
0
0
0
1
1
1
0
0
1
0
2
0
0
1
2
0
3
0
0
0
3
0
e
d
c
b
a
R
=
4
0
0
0
0
0
3
3
3
3
0
3
5
1
6
0
3
1
14
0
0
3
6
0
9
2
e
d
c
b
a
R
=
a b c d e
8
0
0
0
0
0
9
9
18
9
0
9
5
31
3
0
10
31
5
42
0
9
3
42
0
3
e
d
c
b
a
R
=
Например, из вершины а в вершину d идут три маршрута
длиной 2:
a1b8d, a2b8d, a3b8d
и девять маршрутов длины 3:
a1b4c6d, a1b5c6d, a2b4c6d, a2b5c6d, a3b4c6d,
a3b5c6d, a1b8d7d, a2b8d7d, a3b8d7d,
d
e
62
а из d8d идет один маршрут длины 1: d7d, три маршрута длины 2:
d6c6d, d7d7d, 8b8d. При исследовании взаимной достижимости
вершин имеем:
1
0
0
0
0
0
1
1
1
0
0
1
0
1
0
0
1
1
0
1
0
0
0
1
0
=
R
1
0
0
0
0
0
1
1
1
1
0
1
1
1
1
0
1
1
1
0
0
1
1
0
1
1
=
R
1
0
0
0
0
0
1
1
1
1
0
1
1
1
1
0
1
1
1
1
0
1
1
1
0
3
=
R
1
0
0
0
0
0
1
1
1
1
0
1
1
1
1
0
1
1
1
1
0
1
1
1
1
5
4
=
= R
R
Маршрут x
0
u
1
x
1
u
2
x
2
...x
l–1
u
l
x
l
называется цепью, если ребра
u
1
,u
2
...,u
l
все различны. Циклическая цепь x
0
=x
l
при l>=1 называ-
ется
циклом
.
Цепь называется простой, если все ее вершины
различны; при x
0
=x
l
и l>=1 имеем простой цикл.
В графе на рисунке 3.1 маршрут a1b4c4b8d (циклический) не
является цепью, а значит, и циклом; цепи е9е10 (цикл), a2b4c6d8b
(не цикл) не простые, цепь a2b4c6d – простая, а цепи e9e и b4c6d8b
– простые циклы.
ЛЕММА: Всякий маршрут (в частности всякая цепь) графа
содержит хотя бы одну простую цепь, соединяющую ту же пару
вершин. Всякий цикл содержит простой цикл.
Следствие. Всякий кратчайший маршрут между двумя за-
данными вершинами графа есть простая цепь. Всякий цикл наи-
меньшей длины при заданной вершине является простым.
Алгоритм выявления всех маршрутов заданной длины
и цепей
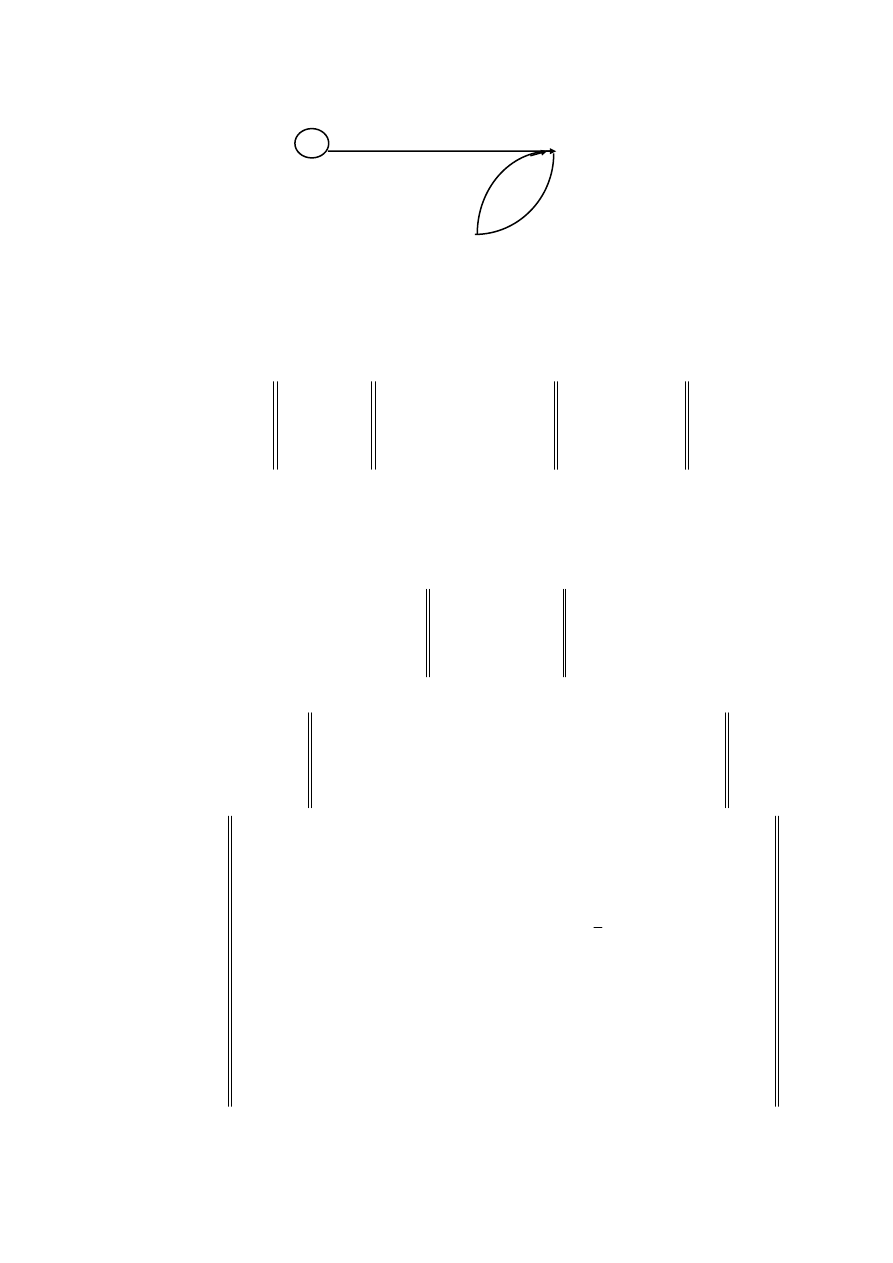
Рассмотрим алгоритм выявления всех маршрутов фиксиро-
ванной длины, идущих из одной заданной вершины графа в дру-
гую на примере графа, изображенного на рисунке 3.1.2.
63
a v b
u
w
t
c
Рис. 3.1.2
Матрица смежности и матрица инциденций А этого графа
имеют вид:
a b c u v w t
0
2
0
2
0
1
0
1
1
c
b
a
R
=
c
b
a
A
θ
ξ
θ
η
η
ξ
ζ
0
0
0
0
0
=
Введем в рассмотрение так называемую «усовершенство-
ванную матрицу смежности» Ru, которая указывает не только на
количество ребер, соединяющих заданную пару вершин, но и на
сами эти ребра:
0
0
0
0
t
w
t
w
v
v
u
Ru
+
+
=
Теперь последовательно возводим матрицу Ru в степень:
tw
wt
t
u
tv
wv
tw
wt
t
w
v
uv
vt
vw
uv
v
u
u
R
+
+
+
+
+
+
+
+
+
+
=
2
2
2
2
2
2
2
0
0
0
2
3
2
2
2
3
2
2
2
3
2
2
3
2
3
2
2
2
3
2
2
2
3
2
2
2
3
3
twt
wt
t
t
w
tw
wtw
w
t
w
tv
wv
tvu
wvu
twt
wt
t
t
w
t
v
tw
wtw
w
t
w
w
v
vuv
twv
wtv
v
t
v
w
v
vu
uvt
uvw
vt
vtw
vwt
vw
v
v
u
uv
u
v
u
u
R
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=

64
Элемент матрицы R
l
u равен сумме таких произведений, в
каждом из которых сомножители соответствуют в том же поряд-
ке последовательным ребрам некоторого маршрута длины l из
i-ой вершины в j-ую, причем ни один маршрут не может быть
пропущен и ни один не повторяется. Например, элемент матрицы
R
2
u:
r
(2)
22
=v
2
+w
2
+t
2
+wt+tw
выявляет последовательность ребер во всех маршрутах длины 2
из вершины b в эту же вершину b (последовательность вершин
каждого маршрута однозначно восстанавливается с помощью
матрицы инциденций А): эти маршруты суть
bvavb, bwcwb, bcb, bwctb, btcwb.
Элемент
r
(3)
21
=vu
2
+v
3
+w
2
v+t
2
v+wtv+twv
позволяет выявить все маршруты длины 3 из b в abvauaua,
bvavbva, bwcwbva и т.д.
Сложность элементов в матрицах R
l
u резко возрастает с рос-
том числа l, но виной здесь отнюдь не алгоритм, а сам факт нали-
чия колоссального количества маршрутов в графе.
Для выделения по матрице Ru только цепей, необходимо
после каждого умножения на Ru вычеркивать те слагаемые, в ко-
торых какой-либо сомножитель встречается более одного раза.
Например, для графа, изображенного на рисунке 3.1.2, имеем
tw
wt
tv
wv
tw
wt
vu
vt
vw
uv
u
R
+
+
+
+
=
′
0
0
0
)
(
2
0
)
(
2
2
2
2
2
2
2
2
2
2
2
twt
tv
wt
wtw
tv
wv
tvu
wvu
w
t
twt
wtv
t
w
vuv
twv
wtv
vu
uvt
uvw
vt
vtw
vwt
vw
uv
Ru
u
R
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
′

65
0
0
0
0
0
)
(
3
tvu
wvu
twv
wtv
uvt
uvw
vtw
vwt
u
R
+
+
+
+
=
′
Кофман А. и Мальгранж И. предложили близкий по идее и
легко реализуемый на ЭЦВМ алгоритм выявления простых цепей
и циклов.
Алгоритм нахождения кратчайших цепей между
заданными вершинами
Пусть необходимо найти кратчайшие и, следовательно, про-
стые цепи между заданными вершинами х, у графа L.
Помечаем вершину х значком 0; затем все смежные с х не-
помеченные еще вершины помечаем значком 1; далее помечаем
значком 2 каждую такую вершину, которая еще не помечена и
смежна хотя бы с одной вершиной, помеченной значком 1, и т.д.
Как только вершина у окажется помеченной некоторым значком
l>=1, процесс прекращаем.
Теперь каждая кратчайшая цепь ненулевой длины
xu
1
x
1
u
2
x
2
...x
l–1
u
l
y,
соединяющая х с у, ищется следующим образом: за x
l–1
берем лю-
бую вершину, смежную с у и помеченную значком l–1; за U
l
–
любое ребро, соединяющее x
l–1
c у, за x
l–2
берем любую вершину,
смежную с x
l–1
и помеченную значком l–2; за U
l–1
–любое ребро,
соединяющее x
l–2
c x
l–1
, и т.д., до тех пор, пока не дойдем до вер-
шины х.
Алгоритм выявления всех простых цепей и циклов
В рассматриваемом алгоритме, являющемся модификацией
алгоритма, описанного выше, некоторые вершины метятся более
чем одним значком. Помечаем вершину х значком 0. Все смеж-
ные с х – значком 1; при этом, если вершина х смежна сама с со-
бой, т.е. имеет петлю, единица будет ее вторым значком.
Далее метим значком 2 вершину z, где z не имела до этого
значка 2 и смежна хотя бы с одной вершиной, у которой значок 1 –
первый. Затем помечаем значком 3 все те вершины, которые не