ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5657
Скачиваний: 10
71
3.4
Обходы
графа
Рассматривается класс задач, связанных с определением
маршрутов специального вида.
Цепь
X
0
U
1
X
1
U
2
X
2
...X
l–1
U
l
X
l
в графе
L=(X,U,P)
называется
эйлеровой цепью, если множество её рёбер совпадает с
U
; при
Х
0
=
Х
l
имеем эйлеров цикл.
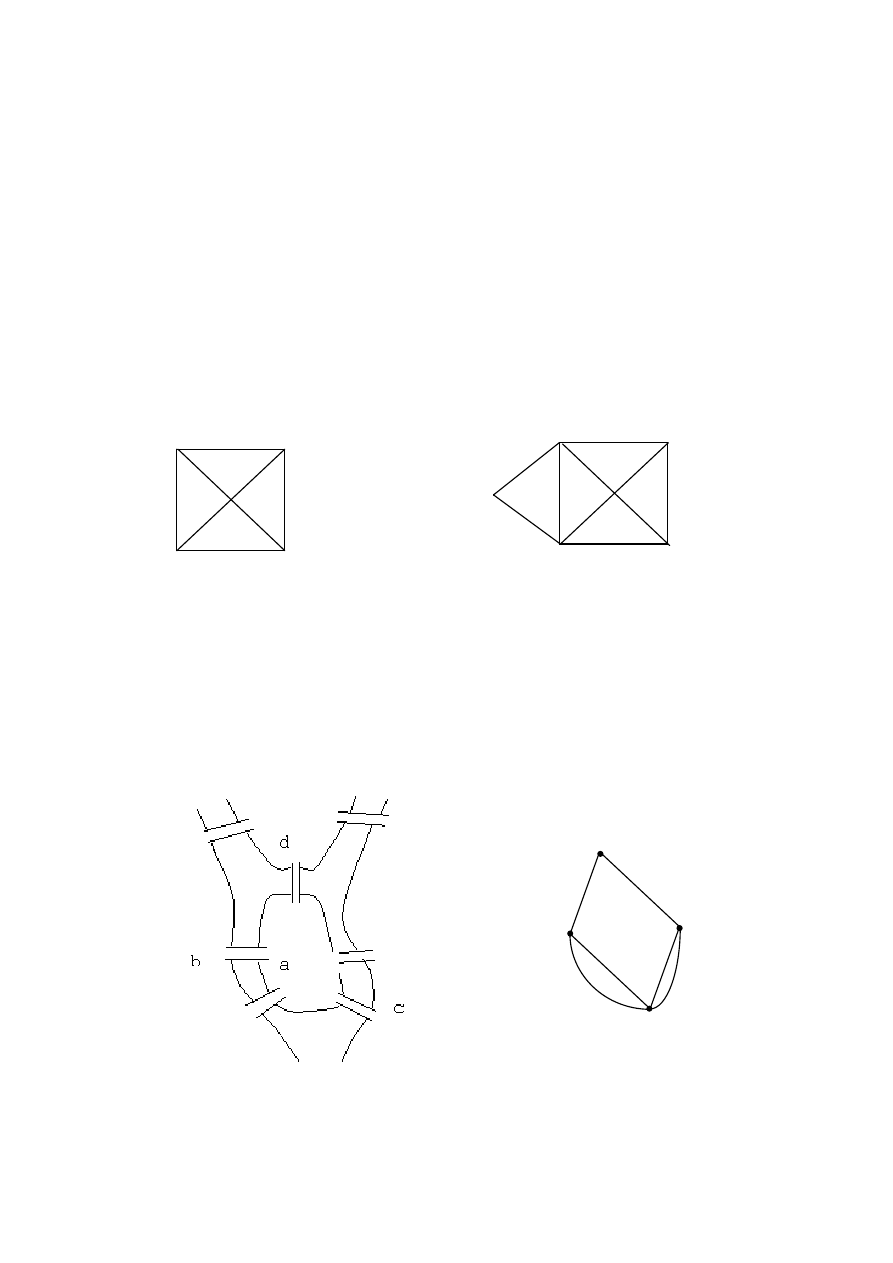
Пример 3.4.1. Можно ли нарисовать графы, изображённые
на рисунке 3.3.1, не отрывая пера от бумаги и не проходя по уже
нарисованным линиям вторично?
а) б)
Рис. 3.4.1
Пример 3.4.2. Через город Калининград протекает река,
омывающая острова. Имеется семь мостов (рис. 3.4.2). Можно ли
обойти все мосты, проходя по каждому из них только один раз?
Рис. 3.4.2
Х
3
B
Х
1
U
Х
2
c
b
d
a

72
Теорема Эйлера (критерий существования эйлеровой це-
пи). Пусть
X
и
Y
– две вершины (не обязательно различные) связ-
ного графа
L=(X,U,P).
Для существования в
L
эйлеровой цепи,
ведущей из
X
в
Y
, необходимо и достаточно, чтобы все отличные
от
X
и
Y
вершины
L
обладали чётными валентностями (число
усиков при вершине), а валентности вершины
X
и
Y
в случае
X=Y
были не чётными.
Доказательство.
Необходимость условий теоремы очевидна, так как если в
графе существует эйлерова цепь, то нечётной валентностью могут
обладать только начальная и конечная вершина (если они не сов-
падают), поэтому число вершин нечётной валентности равно 0
или 2.
Доказательство достаточности проводим по индукции по
числу рёбер графа
m(L)
.
Теперь легко убедиться, что решением примера 3.4.1 для
графа на рисунке 3.4.1, б является цепь
ab
bx
x
x
x
ax
3
1
2
3
1
, а для гра-
фов на рисунке 3.4.1, а и рисунке 3.4.2 задача не разрешима.
Простая цепь
l
l
U
x
x
U
x
U
x
1
2
2
1
1
0
−
…
x
c
графа
L=
(
x
,
U
,
p
),
со-
держащая все его вершины и только по одному разу, называется
гамильтоновой цепью;
при
Хо
=
Хс имеем
гамильтоновый цикл.
Пример 3.4.3.
Пусть граф задаёт сеть коммуникаций между
фиксированным числом пунктов. Необходимо построить мар-
шрут, обеспечивающий посещение всех пунктов по одному и
только по одному разу.
Несмотря на схожесть задач о нахождении эйлеровых цик-
лов и цепей и нахождении гамильтоновых циклов и цепей, реше-
ние последней значительно более сложное.
Известны следующие достаточные условия существования
гамильтоновой цепи и гамильтонового цикла:
1. Если для любых двух несмежных различных вершин Х и
Y связного обыкновенного графа
L
3
)
(
≥
⊂
L
n
)
(
)
(
)
(
L
n
y
S
x
S
≥
+
,
то существует гамильтонов цикл;
2. Если
1
)
(
)
(
)
(
−
≥
+
L
n
y
S
x
S
,

73
то существует гамильтоновая цепь;
3. Если
)
(
5
.
0
)
(
,
)
(
v
l
n
x
S
x
x
⋅
≥
∈
∀
,
то существует гамильтонов цикл.
3.4.1 Алгоритм Флёри нахождения эйлерова цикла
Рассматривая связный граф, все вершины которого удовле-
творяют условиям теоремы Эйлера, строим эйлеровый цикл од-
ним росчерком, придерживаясь следующих правил:
1.Отправляемся из произвольной вершины
α
; каждое прой-
денное ребро зачёркиваем;
2.
В процессе построения не прибегаем к исправлению уже
построенной части траектории;
3.
Никогда не идём по такому ребру, которое в рассматри-
ваемый момент является перешейком, т.е. при удалении которого
граф, образованный не зачеркнутыми рёбрами, распадается на
две компоненты связности, имеющие хотя бы по одному ребру.
Легко показать, что, придерживаясь этих правил, действи-
тельно можно построить эйлеровый цикл.
Действительно, если построен маршрут до вершины Х, то в
оставшемся суграфе (из не зачёркнутых рёбер) имеются две вер-
шины нечётной валентности: Х
и
α
и в силу теоремы Эйлера
имеется эйлеровая цепь, начинающаяся из Х
.
Осталось показать, что всегда, придя в вершину Х,
имеем в
распоряжении не пройденное ребро, не являющееся в данный
момент перешейком. Действительно, если бы все инцидентные Х
рёбра были перешейками, то их было бы по крайней мере два; два
перешейка вели бы в две не связные друг с другом компоненты,
каждая из которых содержит хотя бы одну вершину нечётной ва-
лентноcти. Но это невозможно, так как единственная вершина не-
чётной валентности, не считая Х
,
является вершина
α
.
74
3.4.2 Цикломатическое число
Цикломатическое число
)
(
L
λ
графа
L(X,U,P)
равно
)
(
)
(
)
(
)
(
L
L
n
L
m
L
χ
λ
+
−
=
, где
n(L)=|X|, m(L)=U,
а
χ
(L)
−
число
компонент связности.
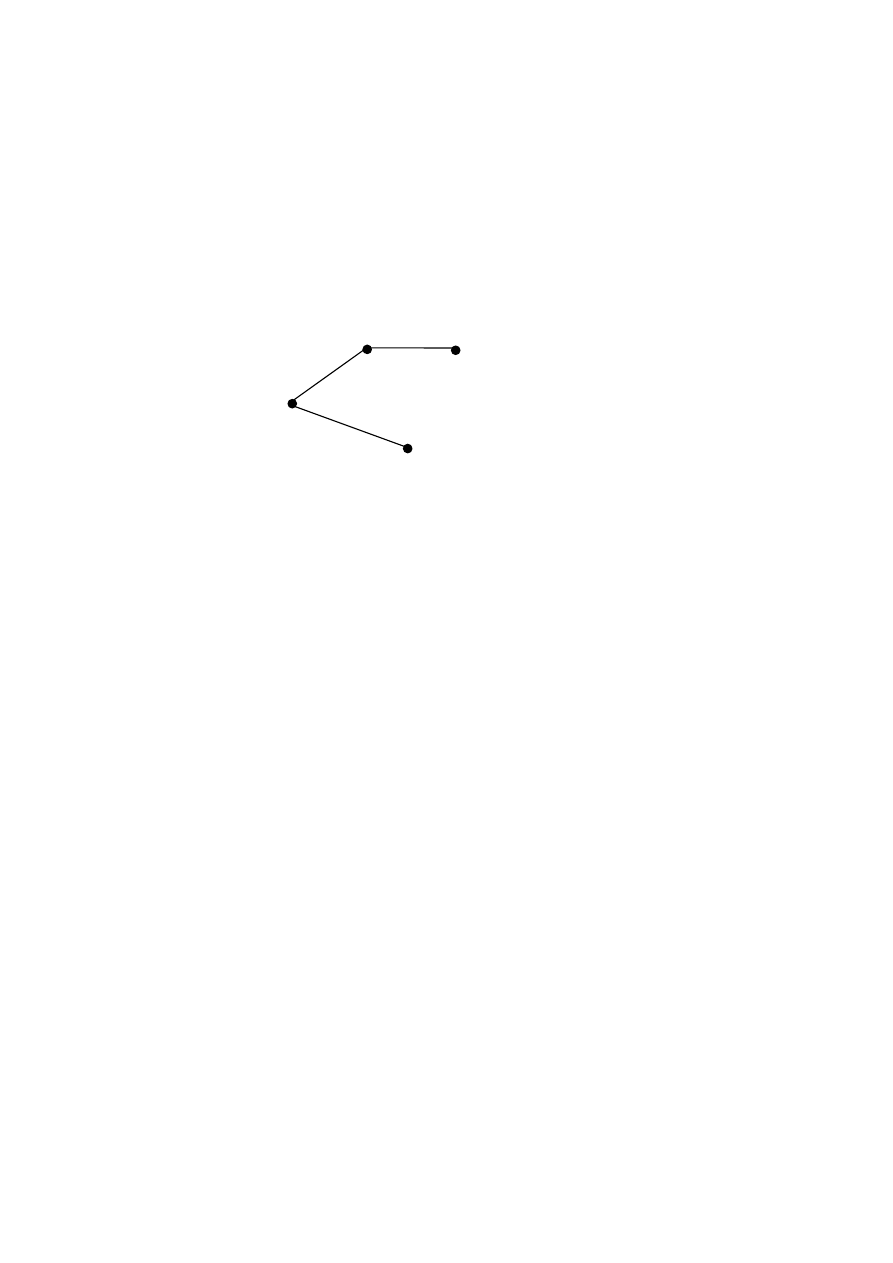
Пример 3.1.4.
n =
4
; m =
3
,
χ
=
1;
( )
0
=
L
λ
.
Рис. 3.4.3
Рассмотрим ряд свойств цикломатического числа.
Пусть
L’=(X,U\{U},P)
–суграф, полученный из
L
удалением
ребра
U
, тогда
( )
( )
( )
⎩
⎨
⎧
+
=
′
случае.
противном
в
,
L,
в
перешеек
-
U
если
,
1
L
λ
L
L
λ
χ
Так как n(L’)=n(L) и m(L’)=m(L)–1, то
( )
( )
( )
⎩
⎨
⎧
=
′
случае.
противном
в
1,
-
перешеек,
-
U
если
,
L
λ
L
L
λ
χ
Пусть Е =
L
=
(X
,
∅,
P)
т.е. пустой граф;
n(L) = n, m(L) =
0,
χ
(E)
=
n
, то
λ
(E)
= 0.
Следовательно,
λ
(
L
)
≥0, где
L
произвольный граф, т.к. при
удалении m
(L)
рёбер
λ
(
L
) = 0 может только уменьшиться у про-
извольного графа
λ
(L)
= 0 тогда и только тогда, когда все уда-
ляемые рёбра
− перешейки, т.е.
L
не содержат циклов.
Теорема. Если
L L
L
1
2
,
,…
χ
компоненты связности графа
L
, то
∑
=
=
χ
λ
λ
1
)
(
)
(
i
i
L
L
.

75
Доказательство.
.
)
(
]
1
)
(
)
(
[
)
(
)
(
)
(
)
(
)
(
)
(
1
1
1
∑
∑
∑
∑
=
=
=
=
+
−
=
=
+
−
=
+
−
=
χ
χ
χ
λ
χ
χ
λ
i
i
i
i
i
i
i
i
L
L
n
L
m
L
n
L
m
L
L
n
L
m
L
3.5
Графы
без
циклов
Рассматриваются графы с нулевым хроматическим числом.
Теорема.
Следующие высказывания равносильны:
− граф
L
не содержит циклов;
− граф
L
не содержит простых циклов;
− никакие две вершины
X
и
Y
в указанном порядке не могут
соединяться более чем одной цепью.
Связаный граф, не содержащий циклов, называется дере-
вом.
Дерево обладает следующими свойствами:
1.
( )
( )
.
0
&
1
=
=
L
L
λ
χ
2.
( )
( )
( )
( ) ( )
.
e.
.
т
,
1
&
0
L
n
L
m
L
m
L
n
L
=
=
−
=
λ
3.
Для любой пары вершин
X
и
Y
в указанном порядке суще-
ствует не более чем одна соединяющая их цепь;
4.
( )
1
=
L
χ
, но если из
L
удалить любое ребро, то для полу-
ченного графа
L
–
( )
2
=
−
L
χ
5.
( )
0
=
L
χ
, но если к
L
добавить хоть одно ребро, то для по-
лученного графа
L
+
( )
1
=
−
L
χ
.
Теорема. Из любого графа
L
можно удалить
( )
L
χ
рёбер,
чтобы полученный суграф
T
не имел циклов и обладал тем же
числом компонент связности, что и
L
. Всякий же суграф, полу-
чаемый удалением менее чем
( )
L
χ
рёбер, содержит циклы.
Доказательство. Первое утверждение при
( )
0
=
L
λ
триви-
ально. Пусть теорема доказана для всех графов с цикломатиче-
ским числом и рассмотрим произвольный граф
L
, у которого
( )
1
+
=
L
λ
, так как
( )
0
>
L
λ
, то граф заведомо содержит цикло-