ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5660
Скачиваний: 10
66
имели еще этого значка и смежны с какой-нибудь из вершин,
имеющих 2 в качестве первого значка и т.д.
Продолжаем процесс до тех пор, пока все вершины не полу-
чат хотя бы по одному значку и для каждой вершины, имеющей
первый значок i, все смежные с ней вершины будут содержать i+1
в числе своих значков.
Далее выявляем цепи так же как и в предыдущем алгоритме,
с той лишь разницей, что если уже построена часть цепи (i=1..l;
x
l
=y)
x
i
u
i+1
x
i+1
...x
l–1
u
l
x
l
и вершина x
i
имеет значки j
1
,j
2
,...,j
k
, то за x
i–1
можно взять любую та-
кую вершину, которая отлична от всех x
i
,...x
l,
смежна с x
i
и у кото-
рой первый (!) значок равен одному из чисел j
1
–1, j2–1,...,j
k
–1.
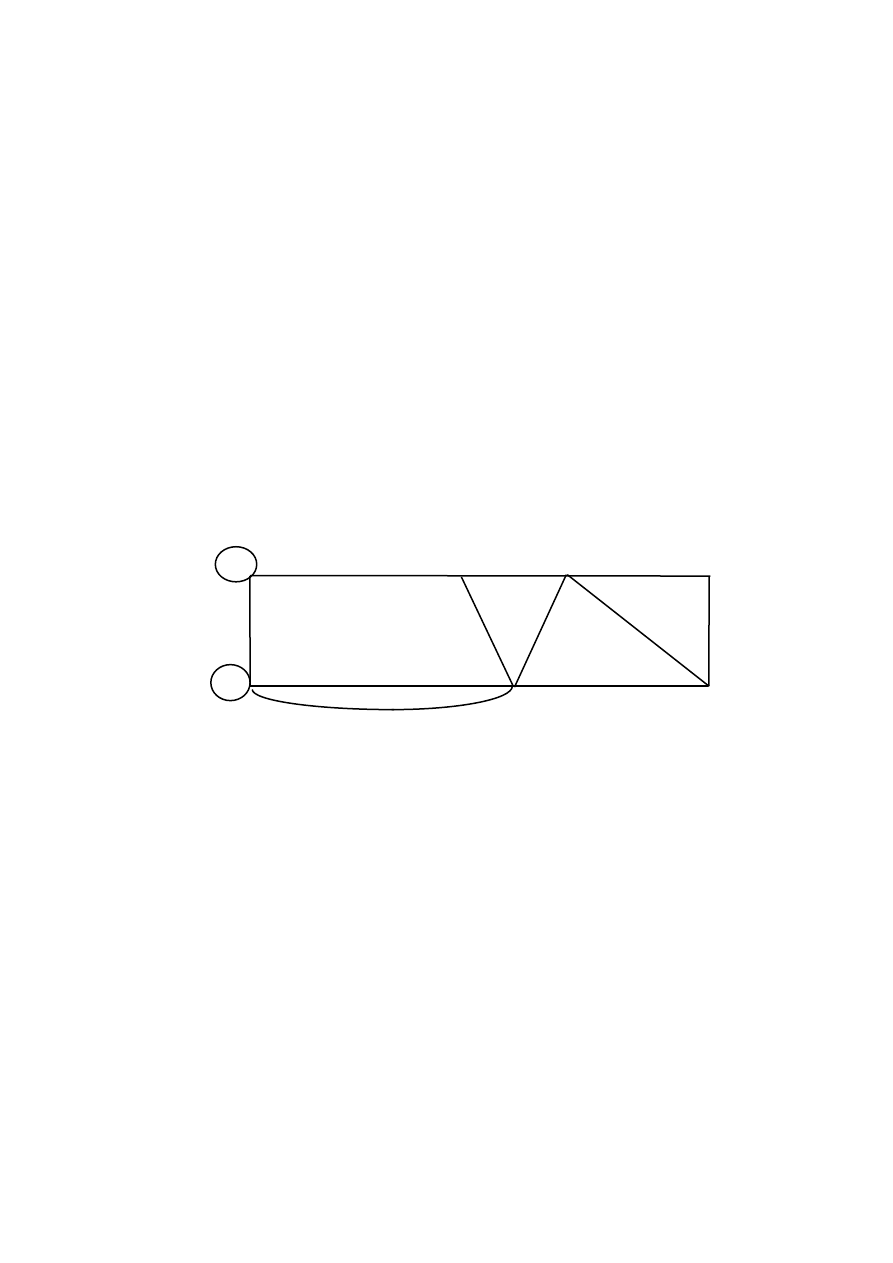
Пример 3.1.1.
u
3
a(1,2,3) b(2,3) c(2,3,4) d(3)
u
4
u
5
u
6
u
2
u
8
u
9
u
10
u
7
u
1
u
11
u
13
x(0,1,2) u
12
e(1,3) y(2,3,4)
Рис. 3.1.3
Разметка осуществлялась следующими шагами:
x
0
x(0,1), a(1), e(1).
x(0,1,2), a(1,2), b(2), c(2), y(2).
a(1,2,3), b(2,3), c(2,3), d(3), e(1,3), e(2,3).
c(2,3,4), y(2,3,4).
В процессе выявления цепей будем указывать не все значки
вершины x
i
, а лишь один или два из них: тот, согласно которому
x
i
выбрана, и тот, который служит для выбора x
i–1
(если он отли-
чен от первого).

67
Последовательность y(2), e(1), x(0) дает две цепи: xu
11
eu
13
y и
xu
12
eu
13
y. Последовательность y(4), d(3), c(2,3), b(2), x(0) дает
цепь xu
6
au
4
bu
5
cu
6
du
7
y и т.д.
Разрешая повторение вершин в последовательности y,x
l–1
,x
l–2
,..,
но запрещая повторение ребер в цепи, мы получим алгоритм вы-
явления всех цепей и циклов, а не только простых.
3.2
Отделимость
и
соединимость
.
Компоненты
связности
Вершины х и у графа L=(x,u,p) называются отделенными,
если не существует никакой соединяющей их цепи, и неотделен-
ными, если хотя бы одна такая цепь имеется. Отношение неотде-
лимости рефлексивно, симметрично и транзитивно, т.е. представ-
ляет собой отношение эквивалентности, и поэтому х разбивается
на классы х
1
, х
2
,...,х
к
попарно неотделимых вершин.
Подграфы L
i
=(x
i
,u
i
,p), порожденные множествами x
i
, не
имеют друг с другом общих вершин и называются компонента-
ми связности. Число их обозначается x(L). При x(L)=1 граф на-
зывается связным.
Рассмотрим матрицу смежности R=R
L
графа над В{0,1} и
обозначим через Е единичную матрицу порядка n(L), образуем
последовательно матрицы
E+R; (E+R)
2
=E+R+R
2
;
(E+R)
3
=E+R+R
2
+R
3
и.т.д.,
элементы которых выражают количество маршрутов длины не
более 1, не более 2, не более 3 и т.д. Для некоторого l
0
, заведомо
не превышающего m(L), будем иметь
(E+R)
lo
=(E+R)
lo+1
.
Каждой системе всех одинаковых столбцов (или строк) «ус-
тановившейся» матрицы (E+R)
lo
отвечает компонента связности
графа L; для ускорения процесса получения установившейся мат-
рицы берут l=2,4,8...
68
Пример 3.2.1.
1
1
0
0
0
1
1
0
0
0
0
0
1
1
1
0
0
1
1
1
0
0
1
1
1
)
(
)
(
4
2
=
+
=
+
E
R
E
R
Отделимость и соединимость
Две несмежные вершины х и у графа L=(x,u,p) называются
К-отделимыми, если из L можно так удалить не более К вер-
шин, чтобы в оставшемся подграфе вершины х и у оказались от-
деленными.
Вершины х и у графа L называются К-соединимыми, если в
L существует К цепей, соединяющих х с у и попарно не имеющих
других общих вершин, а также общих ребер.
Теорема Менгера. В графе L=(x,u,p) две вершины х и у то-
гда и только тогда К-неотделимы, когда они (х+1) соединимы.
Граф называется К-связным, если любые две его вершины
(К–1)-неотделимы.
Вершина, удаление которой приводит к увеличению компо-
нент связности в графе, называется точкой сочленения
.
Ребро u графа L называется
перешейком, если после его
удаления из графа соединяемые им вершины 1-отделимы.
1
1
0
0
0
1
1
0
0
0
0
0
1
1
0
0
0
1
1
1
0
0
0
1
1
0
=
+
E
R
1
2
5
Рис. 3.2.1
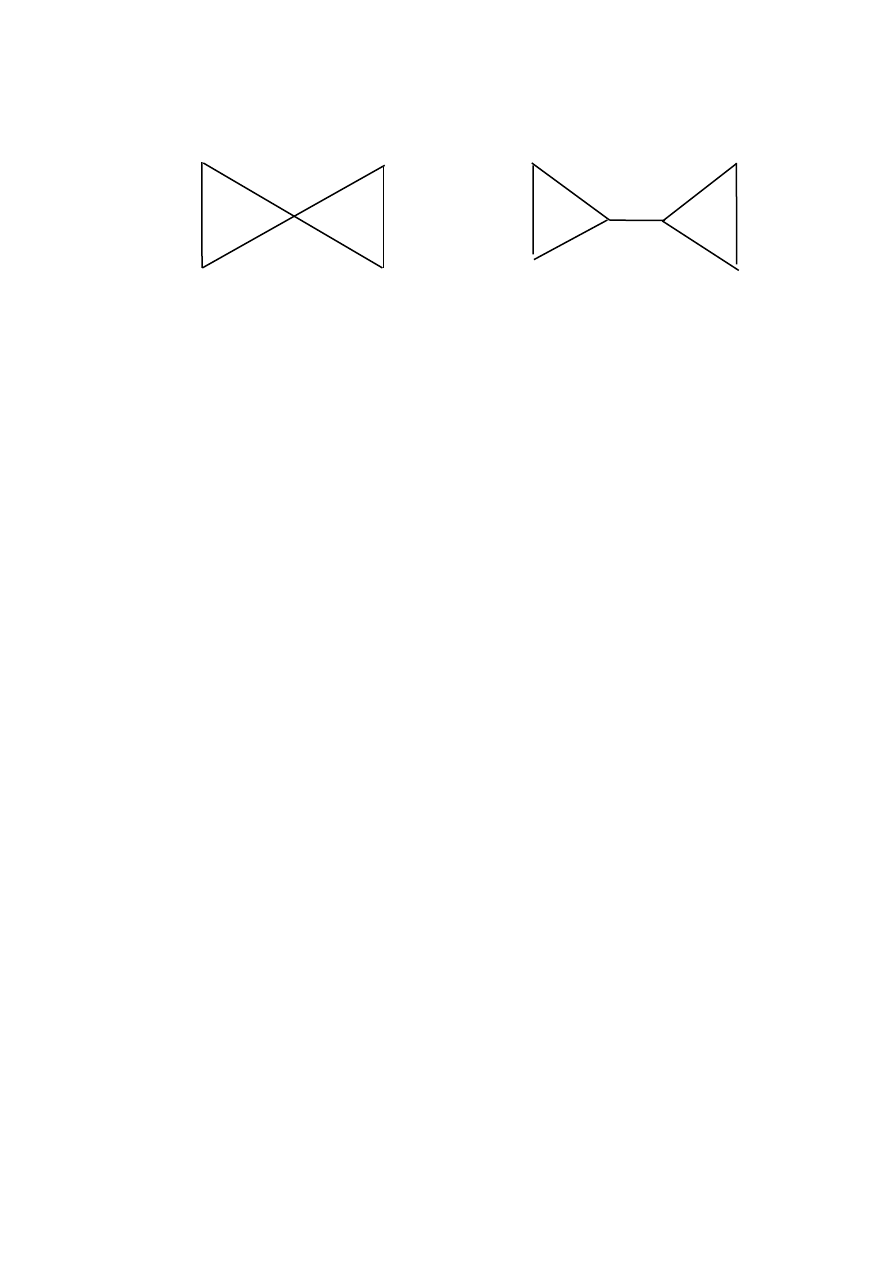
69
Пример 3.2.2.
Графы, изображенные на рисунке 3.2.2, односвязны. Вер-
шина х и ребро u являются соответственно точкой сочленения и
перешейком.
3.3
Метрика
графа
Расстоянием
ρ
L
х,у между вершинами х и у графа L=(x,u,p)
называется длина кратчайшего из маршрутов, соединяющих эти
две вершины; если х и у отделены, то
ρ
L
(х,у)=
∞.
Функция
ρ
L
(х,у) заслуживает названия метрики графа, по-
скольку она удовлетворяет трем аксиомам Фреше:
∀x,y∈x[ρ(х,у)=0 ↔x=y],
∀x,y∈x[ρ(х,у)=ρ(y,x)],
∀x,y,z∈x[ρ(х,у)+ρ(y,z)≥ρ(x,z)].
Выполнение первых двух аксиом очевидно, а третьей (нера-
венство треугольника) легко доказывается.
Для нахождения метрики графа достаточно знать его матри-
цу смежности R над В{0,1}. Далее образуется матрица R+E и по-
следовательно возводится в степень до тех пор, пока не получим
установившуюся
матрицу (E+R)
k
=(E+R)
k+1
=...
Обозначим
(E+R)
l
=||S
(l)
ij
||. Тогда
ρ(x
i
x
j
)=min{l; S
(l)
ij
=1}.
Пример 3.3.1. Для графа на рисунке 3.2.1, например,
ρ(1,2)=1; ρ(1,3)=2 и т.д.
x
u
а)
б)
Рис. 3.2.2
70
1
1
0
0
0
1
1
0
0
0
0
0
1
1
0
0
0
1
1
1
0
0
0
1
1
=
+ E
R
1
1
0
0
0
1
1
0
0
0
0
0
1
1
1
0
0
1
1
1
0
0
1
1
1
)
(
2
=
+ E
R
Метрика однозначно определяет обыкновенный граф и со-
ответственно скелет графа общего вида. Вершина х
0
называется
центральной
,
если
∀x∈x[max
y
∈
x
ρ(x,y)≥ max
y
∈
x
ρ(x
0
,y)],
и
переферийной, если
∀x∈x[max
y
∈
x
ρ(x,y)≤ max
y
∈
x
ρ(x
0
,y)].
Величина
)
,
(
max
min
)
(
y
x
L
r
X
y
X
x
ρ
∈
∈
=
называется радиусом, величина
)
,
(
max
)
(
,
y
x
L
d
X
y
x
ρ
∈
=
диаметром графа.
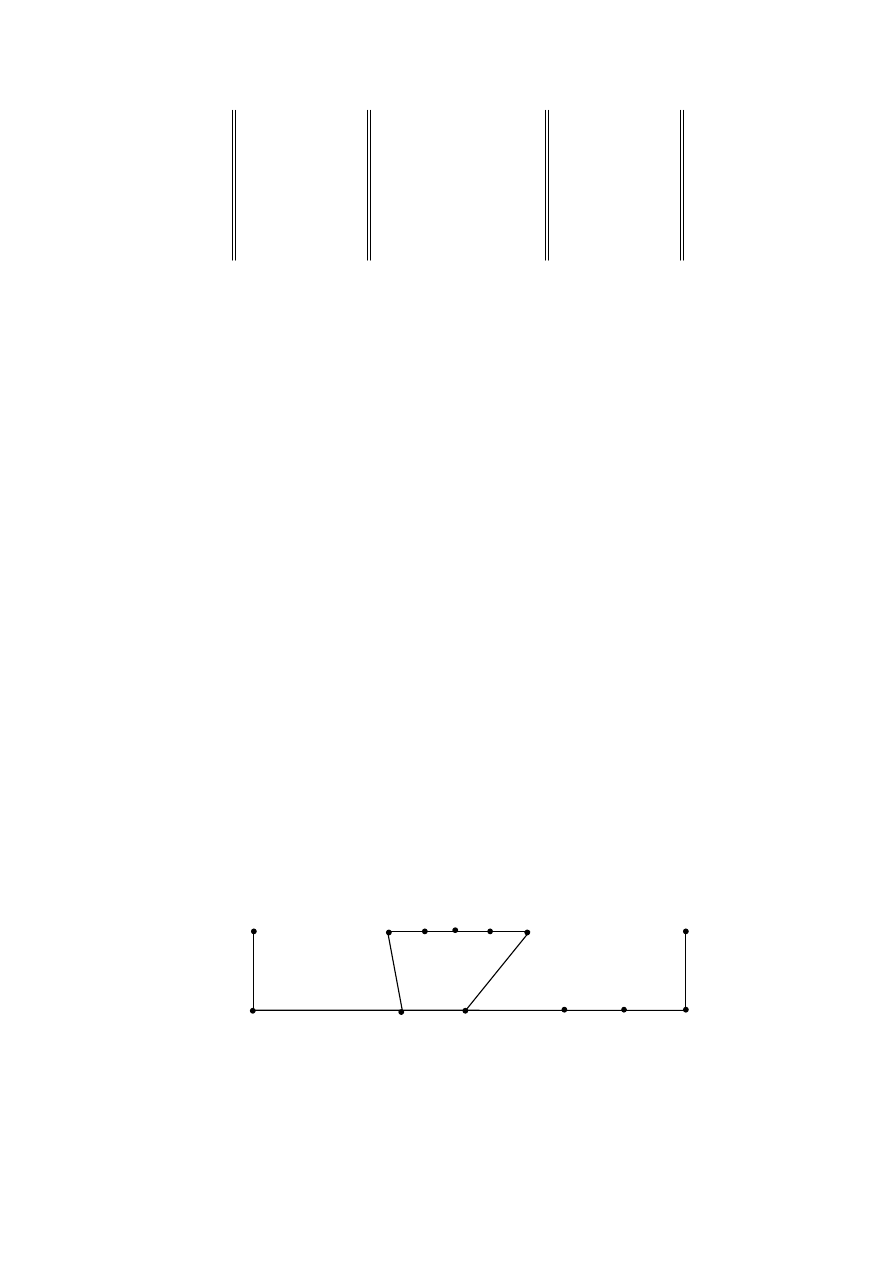
Пример 3.2.1.
У графа, изображённого на рисунке 3.3.1,
вершины
Х
4
и Х
10
– центральные, вершины Х
1
,
Х
7
,
Х
8
,
Х
13
– перифе-
рийные,
r(L)
=4;
d(L)
=7.
X
1
X
9
X
8
X
7
X
6
X
5
X
13
X
2
X
3
X
4
X
10
X
11
X
12
Рис. 3.3.1