ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10277
Скачиваний: 94

26
Обозначение операции проекции
R
)
2
,
3
(
π
. Чтобы выполнить эту опера-
цию, выписываем третье и второе поле всех записей в новую таблицу (вы-
черкнули столбец
1
A
, столбцы
2
A
и
3
A
поменяли местами); одинаковых
строк нет (рис. 1.17, б).
Обозначение операции соединения -
)
(
1
2
1
2
S
R
S
R
B
A
B
A
×
=
≥
≥
σ
.
Результат операции
S
R
×
– девять записей (к каждой строке таблицы R
приписываем строку таблицы S). Вычеркиваем строки, не удовлетворяющие
условию
"
"
1
2
B
A
≥
, т.е. строки, второй элемент которых стоит в алфавите
раньше четвертого (на рис. 1.17, в).
1.3.5. Контрольные вопросы и упражнения
1.
При каких условиях таблица является аналогом
n
-арного отноше-
ния?
2.
Что называется степенью такого отношения?
3.
Какие отношения в реляционной алгебре называются совместимы-
ми?
4.
Составьте конкатенацию записей “ пас ” и “ тор ”.
5.
Отношение
R
имеет степень 3, отношение
S
– 4. Какую степень бу-
дет иметь отношение
S
R
×
?
6.
Операция проекции отношения
R
на список столбцов обозначается
_____________________ .
7.
Как выполняется операция селекции отношения
R
по условию
F
?
8.
Какие операции и в каком порядке нужно выполнить:
))
(
(
2
1
)
2
,
3
(
S
R
A
A
∪
<
σ
π
?
27
1.4. Конечные и бесконечные множества
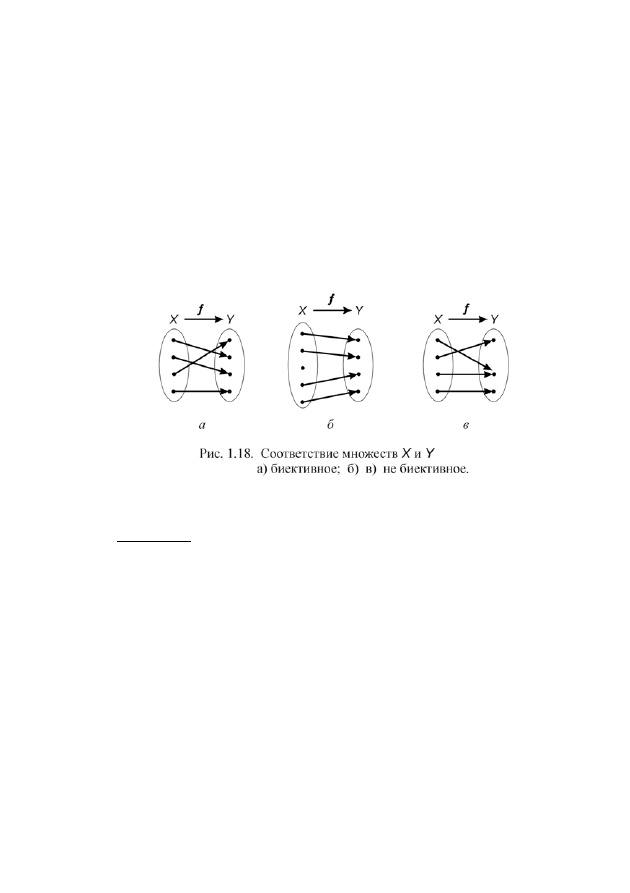
1.4.1. Биекция
В дальнейшем мы будем использовать понятие взаимно однозначного
отображения (биекции). Напомним, что отображение
Y
X
f
→
:
является
биекцией тогда и только тогда, когда каждый элемент
х
множества
Х
имеет
единственный образ
Y
x
f
y
∈
=
)
(
, а каждый элемент
Y
y
∈
имеет един-
ственный прообраз
X
x
∈
, т.е.
)
(
1
y
f
x
−
=
. Так, соответствие между множе-
ствами
X
и
Y
на рис. 1.18, а является биекцией, а на рис. 1.18, б, в – не является
биекцией (объясните почему).
1.4.2. Равномощные множества
Определение. Будем говорить, что множества
X
и
Y
равномощны, если
существует биекция множества
X
на множество
Y
.
Пример. Покажем, что множества
]
1
;
0
[
=
X
и
]
3
;
1
[
=
Y
равномощны.
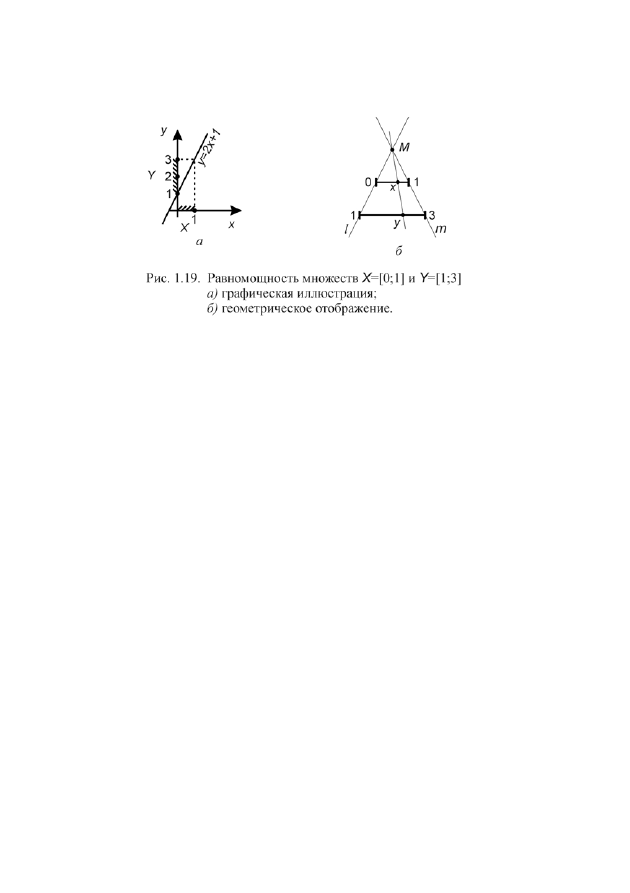
Действительно, можно установить биекцию
Y
X
f
→
:
, например, по закону
1
2
+
= x
y
(рис. 1.19, а). Биекцию между множествами
X
и
Y
можно устано-
вить и геометрически (рис. 1.19, б). Через левые концы отрезков проведена
прямая
l
, через правые – прямая
m
. Точка пересечения прямых
l
и
m
обозна-
чена
М
. Из точки
М
проводим лучи, пересекающие оба отрезка; при этом точ-
ке пересечения с лучом на первом отрезке соответствует единственная точка
пересечения с лучом на втором отрезке (и наоборот).
28
1.4.3. Классы равномощных множеств
Введенное в 1.4.2 отношение равномощности является отношением эк-
вивалентности “
≡ “. В самом деле, оно рефлексивно: для каждого множества
Х
справедливо
X
X
≡
(
Х
равномощно
Х
), так как существует тождественное
отображение множества
Х
на множество
Х
. Это отношение симметрично:
если существует биекция
X
на
Y
, то обратное отображение также является
биекцией (если
Y
X
≡
, то
X
Y
≡
). Отношение транзитивно: если существует
биекция
Y
X
f
→
:
и существует биекция
Z
Y
g
→
:
, то соответствие
))
(
(
x
f
g
z
=
отображает
X
на
Z
биективно (если
Y
X
≡
и
X
Y
≡
, то
Z
X
≡
).
По свойству отношения эквивалентности (см. 1.2.5) получаем разбиение
всех множеств на непересекающиеся классы равномощных множеств. Каждо-
му классу присвоим название - кардинальное число. Таким образом, карди-
нальное число – это то общее, что есть у всех равномощных множеств. Обо-
значим кардинальное число множества
X
card
X
−
или
⏐
Х
⏐
. Пустое мно-
жество имеет кардинальное число
card
∅
=0; для всех конечных множеств
кардинальное число совпадает с количеством элементов множества; а для обо-
значения кардинального числа бесконечных множеств используется буква
ℵ
(алеф). Понятие кардинального числа (мощности множества) обобщает поня-
тие “ количество элементов ” на бесконечные множества.
1.4.4. Сравнение множеств по мощности
Расположим классы эквивалентности равномощных множеств в порядке
возрастания кардинальных чисел:
…
…
…
,
2
1
0
,
,
,
,
,
,
2
,
1
,
0
ℵ
ℵ
ℵ
n
.
29
Для конечных множеств это не вызывает затруднений:
Y
X
<
означает
для конечных множеств, что количество элементов множества
X
меньше ко-
личества элементов множества
Y,
и класс
⏐X⏐
расположен левее класса
⏐Y⏐
в последовательности классов равномощных множеств. А что означает нера-
венство
⏐X⏐<⏐Y⏐
для бесконечных множеств? Договоримся о следующих
обозначениях:
1) если множества
X
и
Y
попадают в один класс эквивалентности, пишем
⏐X⏐=⏐Y⏐
;
2) если класс эквивалентности множества
X
находится левее класса экви-
валентности
Y
в ряду кардинальных чисел, используем обозначение
⏐X⏐<⏐Y⏐
;
3) если класс эквивалентности множества
X
находится правее класса эк-
вивалентности множества
Y
, то
⏐X⏐>⏐Y⏐
;
4) в теории множеств строго доказано, что случай, когда множества
X
и
Y
несравнимы по мощности, невозможен – это означает, что классы равно-
мощных множеств можно вытянуть в цепочку без разветвлений по возраста-
нию мощности.
Следующая теорема, приведенная без доказательства, позволяет устанав-
ливать равномощность бесконечных множеств.
Теорема Кантора-Бернштейна. Пусть
X
и
Y
два бесконечных множе-
ства. Если во множестве
X
есть подмножество, равномощное множеству
Y
, а
во множестве
Y
есть подмножество, равномощное
X
, то множества X и
Y
рав-
номощны.
Пример. Пусть
)
;
0
(
],
1
;
0
[
∞
+
=
=
Y
X
. Покажем, что
⏐X⏐=⏐Y⏐
.
Непосредственно биекцию
X
на
Y
построить трудно, т.к.
X
- отрезок с вклю-
ченными концами, а
Y
– открытый интервал.
Применим теорему Кантора-Бернштейна. Возьмем в качестве подмноже-
ства
1
X
множества
X
открытый интервал :
X
X
=
⊆
=
]
1
;
0
[
)
1
;
0
(
1
. Биекция
1
X
на
Y
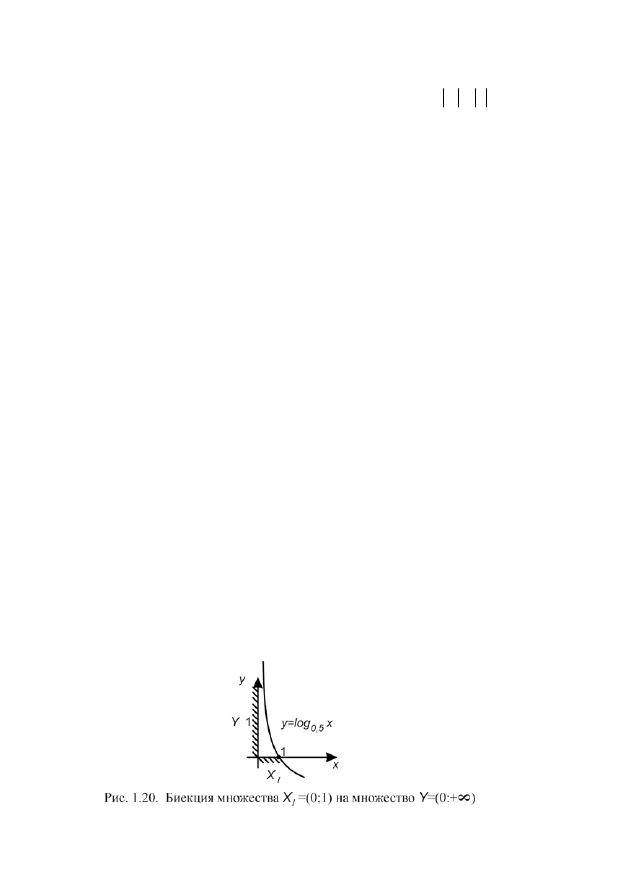
легко устанавливается: например, по закону
x
y
5
,
0
log
=
(рис. 1.20) ,
осуществляется взаимно однозначное отображение интервала (0;1) на интер-
вал
)
;
0
(
+∞
.

30
В качестве подмножества
Y
Y
⊆
1
возьмем любой замкнутый интервал
из
Y
, например,
Y
Y
=
+∞
⊆
=
)
;
0
(
]
3
;
1
[
1
. В 1.4.1 уже показано, что
⏐[1;3]⏐=⏐[0;1]⏐
(существует биекция
1
2
+
= x
y
). Таким образом, условия
теоремы Кантора-Бернштейна выполняются, следовательно, множества
]
1
;
0
[
=
X
и
)
;
0
(
∞
+
=
Y
равномощны (
⏐X⏐=⏐Y⏐
).
1.4.5. Определение конечного множества
Множество
X
называется конечным, если существует биекция
}
,
,
2
,
1
{
:
n
X
f
…
→
, т.е. множество
X
можно взаимно однозначно отобразить
на отрезок натурального ряда {
1,2,…,n}
; при этом
⏐X⏐= n
.
Пустое множество принято относить к конечным множествам и обозна-
чать
⏐∅⏐=0.
Все множества, для которых такую биекцию установить невозможно, бу-
дем называть бесконечными.
1.4.6. Свойства конечных множеств
Сформулируем свойства конечных множеств в виде теорем (не все тео-
ремы будут строго доказаны).
Теорема (правило суммы). Пусть множество
X
является объединением
r
непересекающихся конечных множеств
r
i
X
i
…
,
2
,
1
,
=
. Тогда
∑
=
=
r
i
i
X
X
1
.
Согласно условию теоремы система множеств
}
,
,
,
{
2
1
r
X
X
X
…
являет-
ся разбиением множества
X
. Доказательство проведем методом математиче-
ской индукции по числу
r
блоков разбиения.
Шаг 1. Покажем, что теорема справедлива при
2
=
r
. Пусть
=
∩
∪
=
2
1
2
1
,
X
X
X
X
X
∅
и множества
2
1
,
X
X
конечны, т.е. существует
биекция
}
,
,
2
,
1
{
:
1
1
n
X
f
…
→
и
}
,
,
2
,
1
{
:
2
2
n
X
f
…
→
. Установим биекцию
}
,
,
2
,
1
{
:
2
1
n
n
X
f
+
→
…
следующим образом: всем элементам множества
1
X
оставим прежние номера, а номера элементов множества
2
X
увеличим на
число
1
n
. Полученное отображение
⎩
⎨
⎧
∈
+
∈
=
2
2
1
1
1
),
(
;
),
(
)
(
X
x
если
x
f
n
X
x
если
x
f
x
f