ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9329
Скачиваний: 24
136
D
=
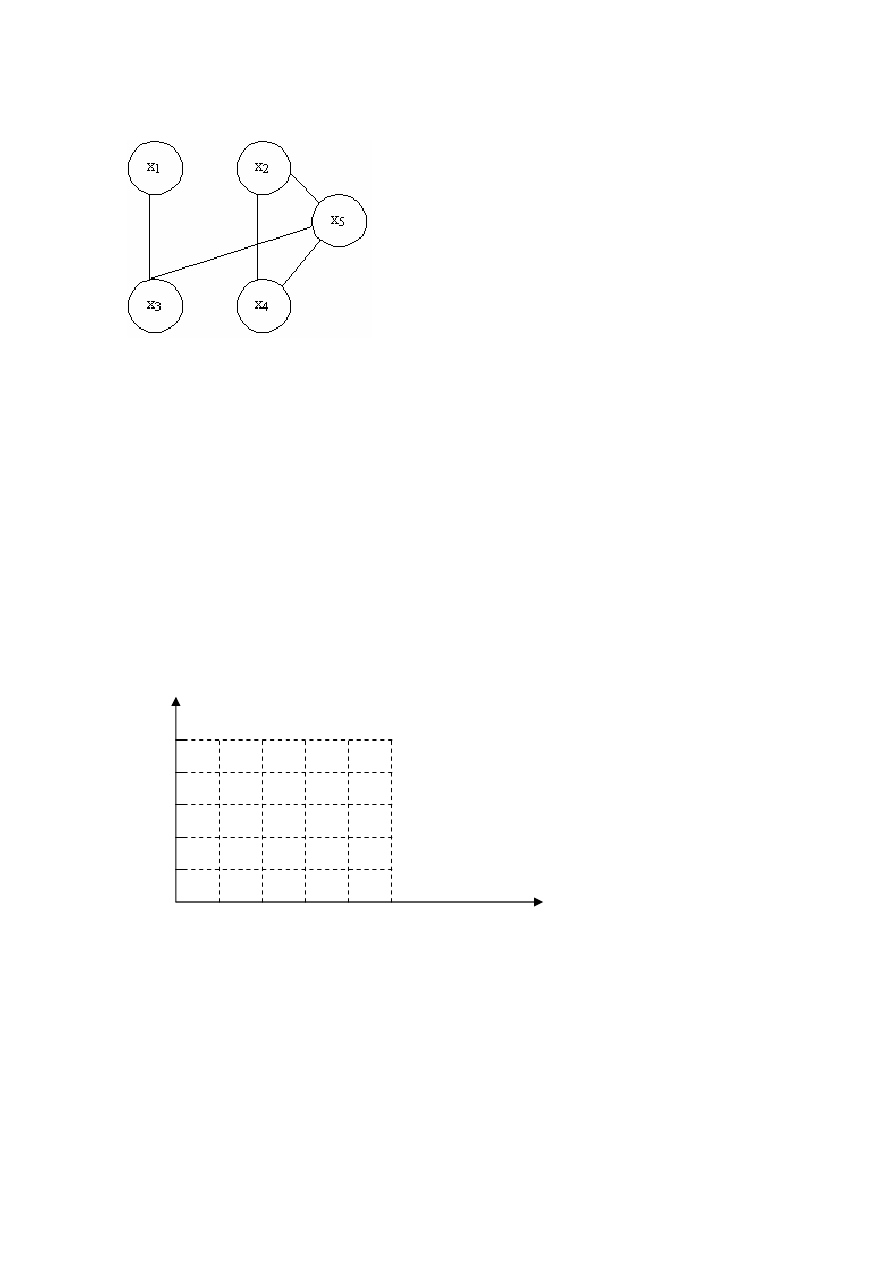
Рисунок 9.24
Диаметр
графа
d(G)
определяется
как
максимальное
рас
-
стояние
между
его
вершинами
.
D(G) = max dij, x
i
x
j
∈ X
Интерес
представляет
нахождение
расстояний
в
графах
ча
-
стного
вида
,
называемых
координатной
решеткой
.
G
r
= (X
r
, U
r
)
В
графе
G
r
= (X
r
, U
r
)
множество
X
r
соответствует
узлам
решетки
,
а
U
r
–
вертикальным
и
горизонтальным
отрезкам
,
со
-
единяющим
узлы
решетки
.
Введем
декартову
систему
координат
с
осями
s
и
t.
t
x
1
x
2
x
3
x
4
x
5
x
6
s
Рисунок 9.25
Расстояние
между
соседними
узлами
решетки
называют
ша-
гом решетки
и
принимают
равным
единице
.
Расстояние
между
двумя
произвольными
вершинами
в
решетке
G
r
рассчитывается
:
d
ij
= |s
i
– s
j
| + |t
i
– t
j
|,
где
s
i
, s
j
и
t
i
, t
j
–
координаты
x
i
и
x
j
.
1 2 3 4 5
1 0 3 1 3 2
2 3 0 2 1 1
3 1 2 0 2 1
4 3 1 2 0 1
5 2 1 1 1 0

137
Обычно
задаются
размеры
решетки
p x q,
где
p –
число
узлов
решетки
по
оси
s, q – not.
Например
, d(7, 13) = |1 – 2| + |5 – 0| = 6.
Граф
G
r
удовлетворяет
аксиомам
Фреше
.
Если
произволь
-
ный
граф
G
отображается
в
G
r
так
,
что
любые
вершины
G
разме
-
щаются
в
узлах
решетки
,
то
расстояние
между
вершинами
G
оп
-
ределяется
как
расстояние
между
соответствующими
узлами
решетки
G
r
.
Любой
граф
G
может
быть
отображен
в
решетку
G
r
.
Для
подсчета
суммарной
длины
L(G)
ребер
графа
G,
ото
-
браженного
в
решетку
G
r
,
введем
понятие
матрицы
геометрии
D
ν
.
D
ν
представляет
собой
часть
матрицы
расстояний
D,
в
кото
-
рой
исключены
элементы
d
ij
,
если
вершины
x
i
x
j
∈ X
не
смежны
в
графе
G.
0,
если
r
ij
= 0;
d
ν
ij
=
d
ij
,
если
r
ij
≠ 0.
Сумма
элементов
матрицы
D
ν
определяет
удвоенную
сум
-
марную
длину
L(G)
ребер
графа
G
при
данном
его
отображении
в
решетку
G
r
.
9.7
Цикломатическое
число
,
раскраска
Наименьшее
число
ребер
,
которое
необходимо
удалить
из
графа
G,
чтобы
он
стал
ациклическим
,
называется
цикломатиче-
ским числом
графа
.
Для
графа
G=(X, U), |X| = n, |U| = m
цикло
-
матическое
число
j(G) = m – n + k,
где
m –
число
ребер
графа
, n –
число
вершин
, k –
число
компонент
связности
графа
.
Для
графа
,
состоящего
из
одной
компоненты
связности
j(G) = m – n + 1,
на
-
пример
,
на
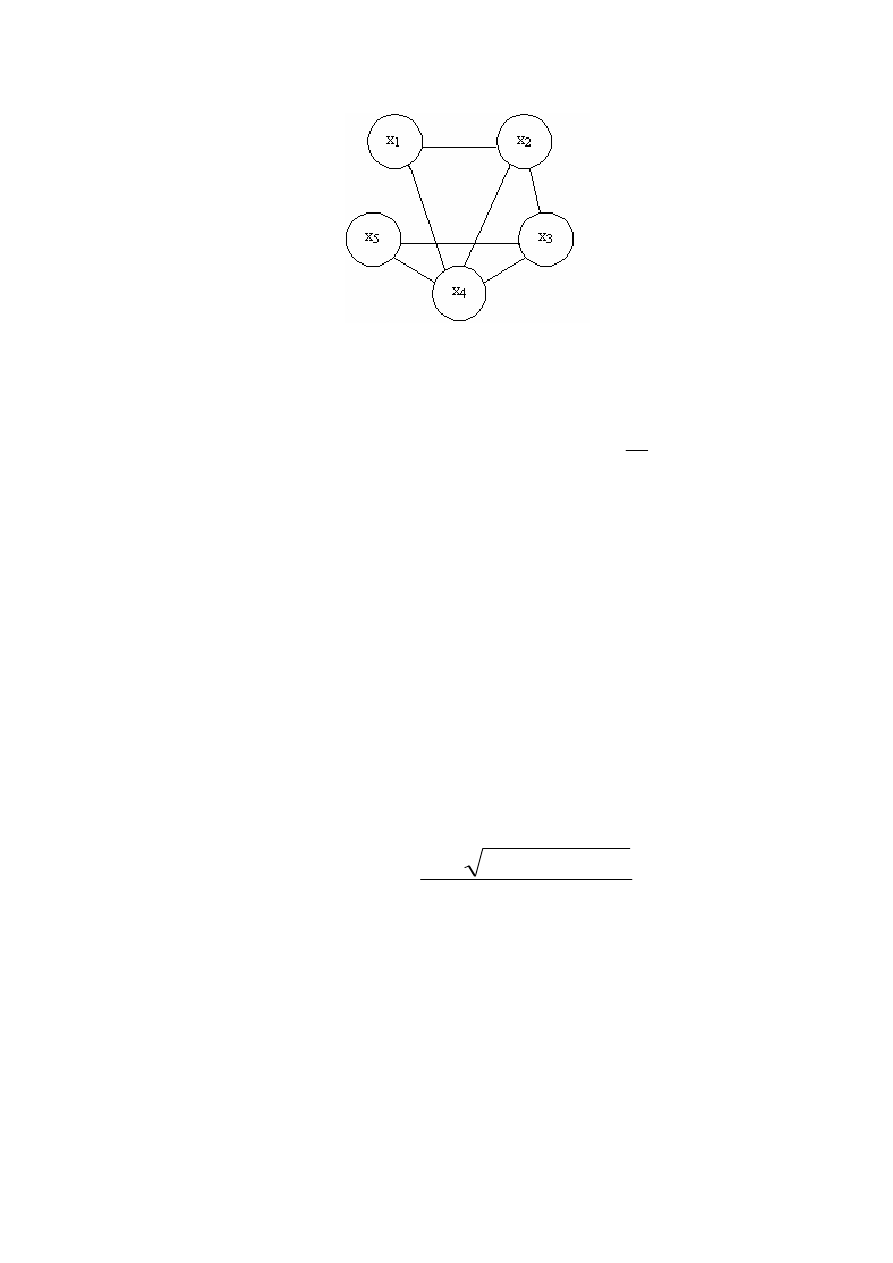
рис
. 9.26 j(G) = 7 – 5 = 2,
т
.
е
.
после
удаления
двух
ре
-
бер
граф
становится
ациклическим
,
в
примере
это
ребра
(
напри
-
мер
, (
х
4
,
х
2
), (
х
4
,
х
3
)).
Чтобы
узнать
,
какие
ребра
удалять
,
необхо
-
димо
каждый
раз
удалять
ребро
,
которое
разрушает
хотя
бы
один
цикл
.
138
Рисунок 9.26
Раскраской
вершин
графа
называется
разбиение
множества
вершин
графа
на
l
непересекающихся
классов
(
подмножеств
)
,
;
,
1
,
;
;
;
,...,
,
1
2
1
j
i
l
j
i
O
X
X
X
X
X
X
X
j
l
i
i
i
l
≠
∈
/
=
=
=
∩
∪
таких
,
что
внутри
каждого
подмножества
Х
i
не
должно
быть
смежных
вершин
.
Если
каждому
подмножеству
Х
i
поставить
в
соответствие
определенный
цвет
,
то
вершины
внутри
подмножества
можно
окрасить
в
один
цвет
,
вершины
другого
–
в
другой
и
т
.
д
.
до
пол
-
ной
раскраски
.
В
этом
случае
граф
называется
l-
раскрашива
-
емым
.
Наименьшее
число
подмножеств
,
на
которое
разбивается
граф
при
раскраске
,
называется
хроматическим числом K(G).
Очевидно
,
полный
граф
K
n
можно
раскрасить
только
в
n
цветов
K(Kn)=n.
Для
связного
графа
G = (X, U)
с
n–1
≤ m ≤ n(n–1)/2
верх
-
няя
оценка
хроматического
числа
:
Нижней
оценкой
K(G)
является
число
вершин
в
наибольшем
полном
подграфе
графа
G.
Хроматическое
число
обычно
определяется
с
помощью
ме
-
тодов
линейного
программирования
.
Важное
практическое
применение
имеют
2-
раскрашиваемые
или
двудольные
(
граф
Кенига
) (
бихроматические
)
графы
.
Обо
-
значается
двудольный
граф
G
n1,n2
=(X
1
, X
2
, U),
где
X
1
∪X
2
=X,
.
2
)
(
8
9
3
)
(
⎥
⎦
⎤
⎢
⎣
⎡
−
+
+
=
n
m
G
K
139
X
1
∩X
2
=
∅,
а
ребра
соединяют
только
подмножества
X
1
и
X
2
между
собой
.
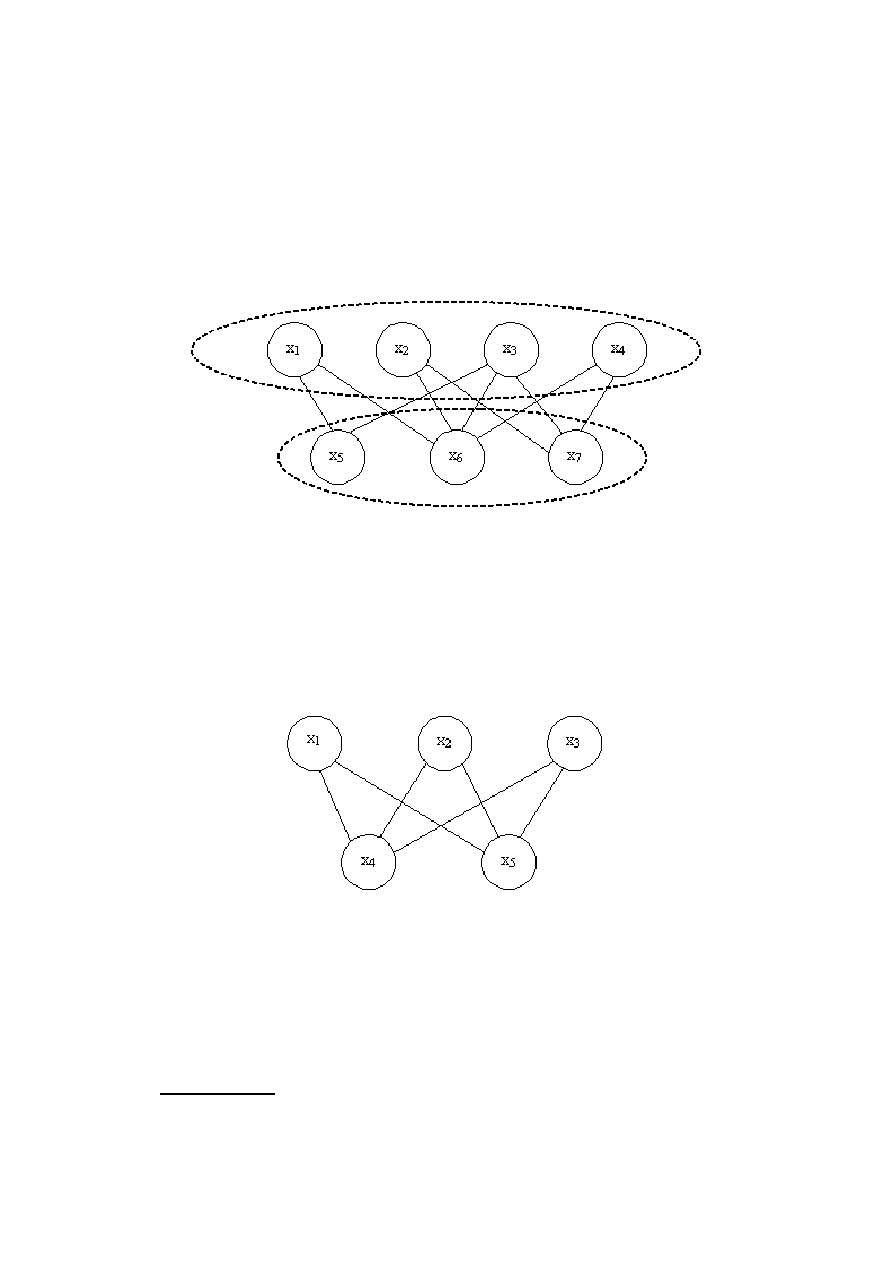
Пример
двудольного
графа
.
G
n1,n2
=(X
1
, X
2
, U); |X
1
| = n
1
= 4;
|X
2
| = n
2
= 3; X
1
= {x
1
, x
2
, x
3
, x
4
};
X
2
= {x
5
, x
6
, x
7
}.
Рисунок 9.27
− Двудольный граф
Граф
K
n1, n2
называется
полным
двудольным
графом
,
если
любая
вершина
x
i
∈X
1
смежна
каждой
вершине
x
j
∈X
2
(i
≠j).
В
двудольном
графе
множество
X
1
можно
раскрасить
од
-
ним
цветом
,
Х
2
–
другим
цветом
.
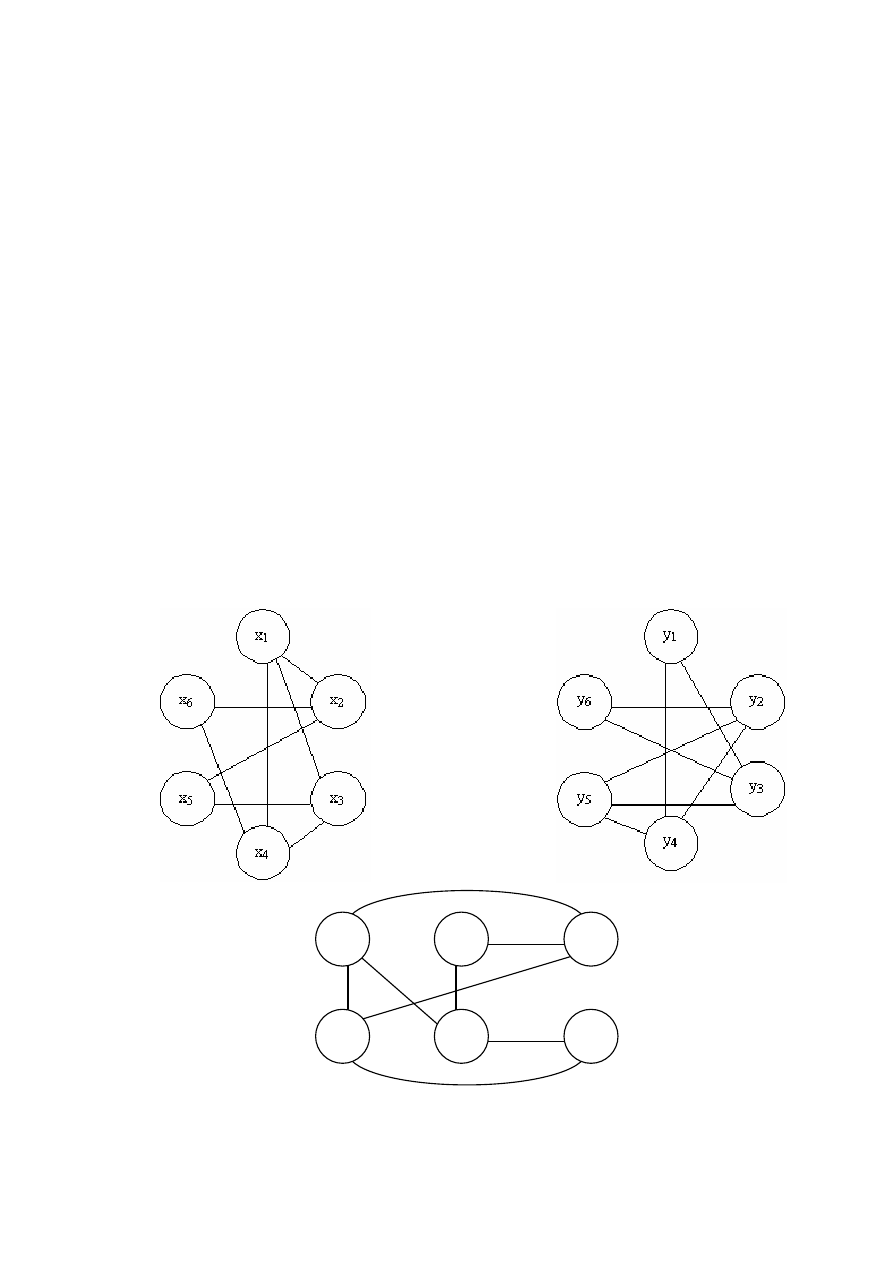
Рисунок 9.28
− Полный двудольный граф К
32
При
разработке
алгоритмов
компоновки
,
размещения
и
трассировки
возникает
необходимость
определения
двудольно
-
сти
некоторого
графа
или
выделения
в
этом
графе
максимальных
непересекающихся
двудольных
частей
.
Теорема 4.
Граф
G
n1, n2
является
двудольным
тогда
и
толь
-
ко
тогда
,
когда
он
не
имеет
простых
циклов
нечетной
длины
.
140
Рассмотрим
число
внутренней
устойчивости
.
Если
любые
вершины
в
графе
G = (X, U) X’
⊆X,
не
смежны
,
то
это
подмноже
-
ство
называется
внутренне устойчивым.
Тождественные
преобразования
графов
,
сводимые
только
к
переобозначению
вершин
и
ребер
,
приводят
к
получению
изо
-
морфных
графов
.
9.8
Изоморфизм
графов
Два
графа
G=(X, U)
и
G’=(X’, U’)
называют
изоморфными,
если
можно
установить
взаимно
-
однозначное
соответствие
X
↔X’, U↔U’
такое
,
что
если
(x
i
, x
j
)
∈X ↔ (x
i
, x
j
)
∈X’,
то
ребро
u = (x
i
, x
j
)
∈U ↔ u’ = (x’
i
, x’
j
)
∈U’.
Изоморфизм
есть
отношение
эквивалентности
на
графах
.
Изоморфные
графы
могут
быть
по
-
лучены
один
из
другого
при
помощи
перенумерации
их
вершин
.
Если
изоморфные
преобразования
проводятся
с
графом
,
задан
-
ным
матрицей
смежности
,
то
они
сводятся
к
перестановке
места
-
ми
соответствующих
строк
и
столбцов
.
а) б)
в)
Рисунок 9.29
− Граф G и изоморфные ему
z
4
z
1
z
5
z
2
z
6
z
3