ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9325
Скачиваний: 24

146
элемента
несколько
раз
.
Например
,
к
числу
комплектов
можно
отнести
{a, b, c}; {a, b, c, c}; {a, a, a}, X= {a, b, c, d}.
Вместо
отношения
включения
,
являющегося
основным
по
-
нятием
теории
множеств
,
в
теории
комплектов
вводится
функция
числа
повторений
каждого
элементов
и
обозначается
(
х
,
В
) (
чита
-
ется
«
число
х
в
В
»).
Если
ввести
ограничения
0
≤ # (x, B) ≤ 1,
для
∀x∈B,
то
получим
обычное
понятие
множества
элементов
.
Приведем
теоретико
-
множественные
операции
,
определен
-
ные
на
комплектах
.
1.
Операция
включения
# (x, B) > 0.
2.
Операция
не
включено
# (x, B) = 0.
3.
Пустое
множество
# (x, B) = 0,
∀x∈
Х
.
4.
А
⊆
В
; # (x,
А
)
≤ # (x, B), ∀x∈
Х
.
5.
А
=
В
; # (x,
А
) = # (x, B),
∀x∈
Х
.
6.
А
∪
В
; # (x,
А
∪
В
) = max{#(x, A), #(x, B)}.
7.
A
∩B; #(x, A∩B) = min{#(x, A), #(x, B)}.
8.
A+B; # (x,
А
+B) = # (x,
А
) +#(x, B).
9.
A–B; # (x,
А
–B) = # (x,
А
) – #(x, A
∩B).
Под
пространством
комплектов
X
–n
понимают
множество
всех
таких
комплектов
,
элементы
которых
принадлежат
Х
и
ни
один
из
них
не
входит
в
комплект
более
n
раз
:
{B
∈X
–n
}
⇔{x∈B⇒x∉X; #(x,B) ≤ n, ∀x∈X}.
Мощностью
комплекта
В
называется
общее
число
повторе
-
ний
элементов
в
комплекте
.
Сетью
Петри
(
С
)
называется
дискретная
детерминированная
модель
,
состоящая
из
четырех
элементов
С
= (P, T, I, 0),
где
Р
= {
р
1
,
р
2
,…,
р
n
} –
конечное
множество
позиций
n
≥ 0.
T = {t
1
, t
2
,…, t
m
} –
конечное
множество
переходов
m
≥ 0,
P
∩T = ∅.
I : T
→P
∞
–
входная
функция
,
отображающая
множество
пе
-
реходов
в
комплекты
событий
.
0 :
Т
→P
∞
–
выходная
функция
из
Т
в
P
∞
.
Позиция
р
i
является
входной
позицией
перехода
t
j
в
том
случае
,
если
p
i
∈I(t
j
),
и
вы
-
ходной
,
если
p
i
∈0(t
j
).
∑
∈
=
x
X
x
B
x
B
.
),
,
(
#
147
Расширенными
входными
и
выходными
функциями
сетей
Петри
соответственно
называются
отображения
:
I : P
→T
∞
; 0 : P
→T
∞
,
для
которых
#(t
j
, I(p
i
)) = #(p
i
, 0(t
j
)); #(t
j
, 0(p
i
)) = #(p
i
, I(t
j
).
Пример
.
Пусть
структура
сети
Петри
имеет
вид
:
С
= (P, T, I, 0); P = {p
1
, p
2
, p
3
, p
4
, p
5
}; T = {t
1
, t
2
, t
3
, t
4
};
I(t
1
) = {p
1
}
0(t
1
) = {p
2
, p
3
, p
5
}
I(t
2
) = {p
2
, p
3
, p
5
} 0(t
2
) = {p
5
}
I(t
3
) = {p
3
}
0(t
3
) = {p
4
}
I(t
4
) = {p
4
}
0(t4)
=
{p
2
, p
3
}
Расширенными
входной
и
выходной
функциями
данной
се
-
ти
являются
:
I(p
1
) = {
∅} 0(p
1
) = {t
1
}
I(p
2
) = {t
1
, t
4
}
0(p
2
) = {t
2
}
I(p
3
) = {t
1
, t
4
}
0(p
3
) = {t
2
, t
3
}
I(p
4
) = {t
3
}
0(p
4
) = {t
4
}
I(p
5
) = {t
1
, t
2
}
0(p
5
) = {t
2
}
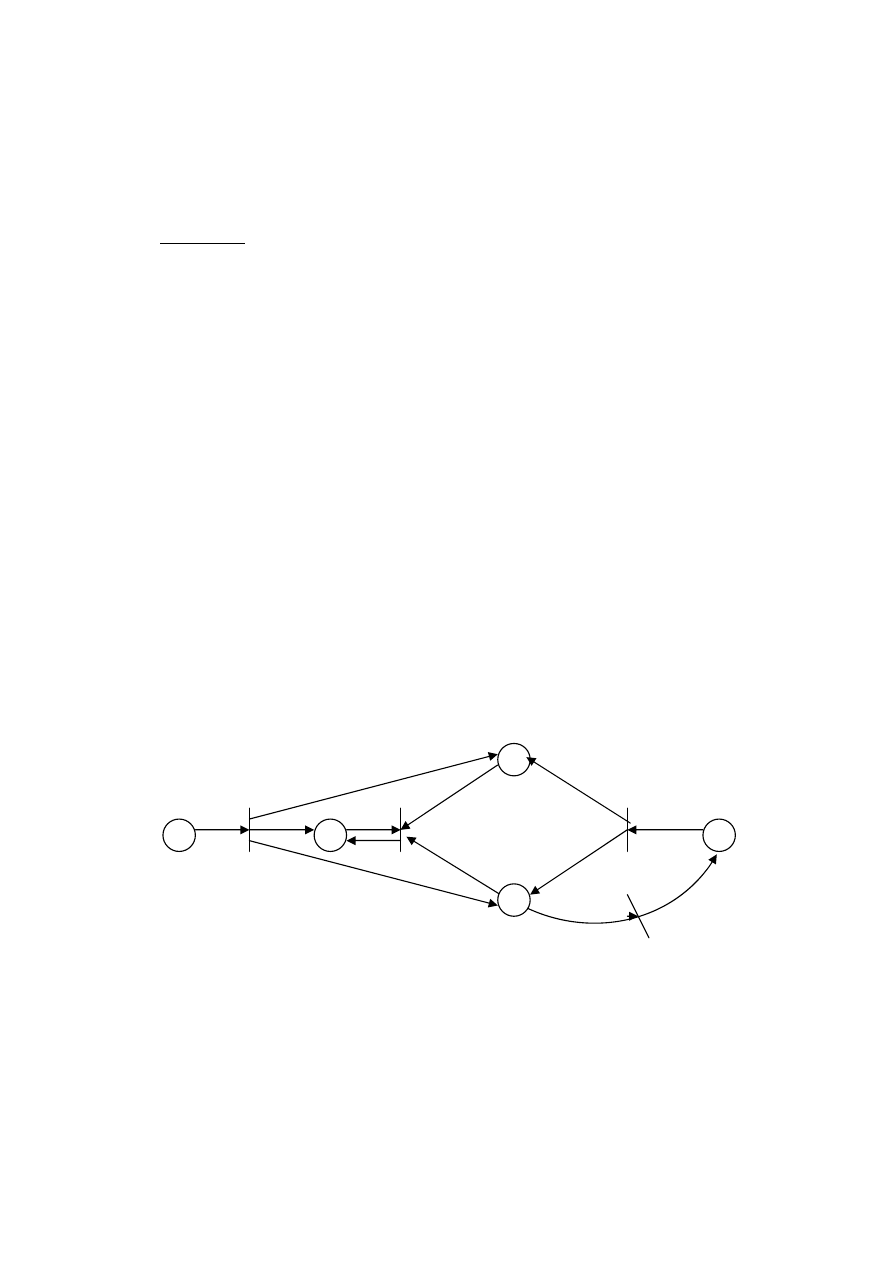
Проиллюстрируем
пример
графически
.
Элементами
графа
служат
кружки
,
обозначающие
позиции
сети
,
и
планки
,
обозначающие
ее
переходы
.
Ориентированные
дуги
соединяют
позиции
и
переходы
в
обоих
направлениях
.
Рисунок 9.33
Граф
G сети Петри –
двудольный
ориентированный
муль
-
тиграф
G = (V, A),
где
V = {v
1
, v
2
, …, v
s
} –
множество
вершин
V =
=P
∪T;
A = {a
1
, a
2
,…., a
r
} –
комплект
направленных
дуг
.
P
3
P
4
P
2
P
5
P
1
t
3
t
4
t
2
t
1
148
а
i
= <v
j
, v
k
>, v
j
, v
k
∈V.
Комплект
направляющих
дуг
А
вводится
следующим
обра
-
зом
:
#((p
i
t), A) = #(p
i
, I(t
j
)),
∀p
i
∈P, t
j
∈T;
#((t
j
, p
i
), A = #(p
i
, 0(t
j
)).
Сеть
можно
выполнить
.
Для
выполнения
сети
применяют
маркировку
,
представляющую
присвоение
позициям
сети
фишек
,
количество
и
положение
которых
при
выполнении
сети
могут
изменяться
.
Маркировкой
μ
сети Петри
С
= (P, T, I, 0)
называется
функция
,
отображающая
множество
позиций
р
в
множество
на
-
туральных
чисел
N:
μ : P → N
Под
маркировкой
можно
подразумевать
n-
вектор
μ = (μ
1
,
μ
2
,…,
μ
n
),
где
n = |P|,
μ
i
∈N, i =1,n,
который
определяет
для
каждой
позиции
сети
Р
i
количество
фи
-
шек
(
μ
i
)
в
этой
позиции
.
На
графе
сети
Петри
фишки
изобража
-
ются
точками
в
кружке
соответствующей
позиции
,
если
число
точек
невелико
,
и
в
противном
случае
указывается
натуральное
число
μ
i
для
данной
позиции
.
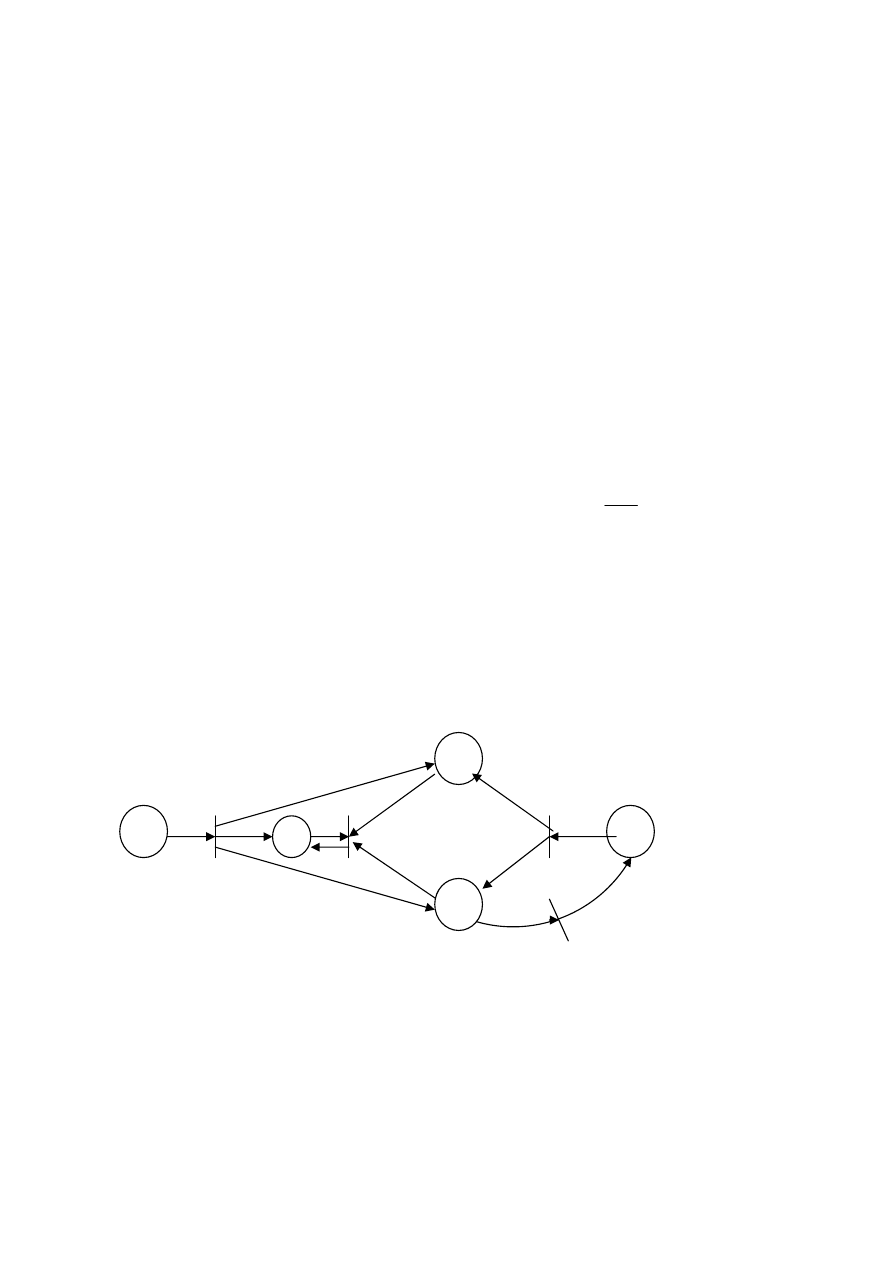
Приведем
пример
маркировки
для
сети
,
заданной
рисунком
9.34.
Рисунок 9.34
Фишки
во
входной
позиции
,
допускающие
переход
,
носят
название
разрешающих
фишек
.
P
3
P
4
P
2
P
5
P
1
t
3
t
4
.
S1
..
149
Переход
t
i
∈T
в
маркированной
сети
Петри
С
= (P, T, I, 0)
с
маркировкой
μ разрешен,
если
μ
i
=
μ(
р
i
)
≥ # (
р
i
,I(t
i
)),
∀
р
i
∈P.
Пример
маркировки
μ = (1, 2, 0, 51, 0) (
рис
. 9.34).
Переход
допускается
удалением
всех
разрешающих
фишек
из
его
входных
позиций
и
последующим
помещением
в
каждую
из
его
выходных
позиций
по
одной
фишке
для
каждой
дуги
.
Запуск
перехода
в
целом
заменяет
маркировку
μ
сети
Петри
на
новую
маркировку
μ’.
Переход
t
i
в
маркированной
сети
Петри
с
маркировкой
μ
может
быть
запущен
,
если
он
разрешен
.
Маркировка
μ’
для
разрешенного
перехода
t
i
образуется
по
правилу
μ’ (
р
i
) =
μ(
р
i
) – #(
р
i
, I(t
i
)) + #(
р
i
, 0(t
i
)).
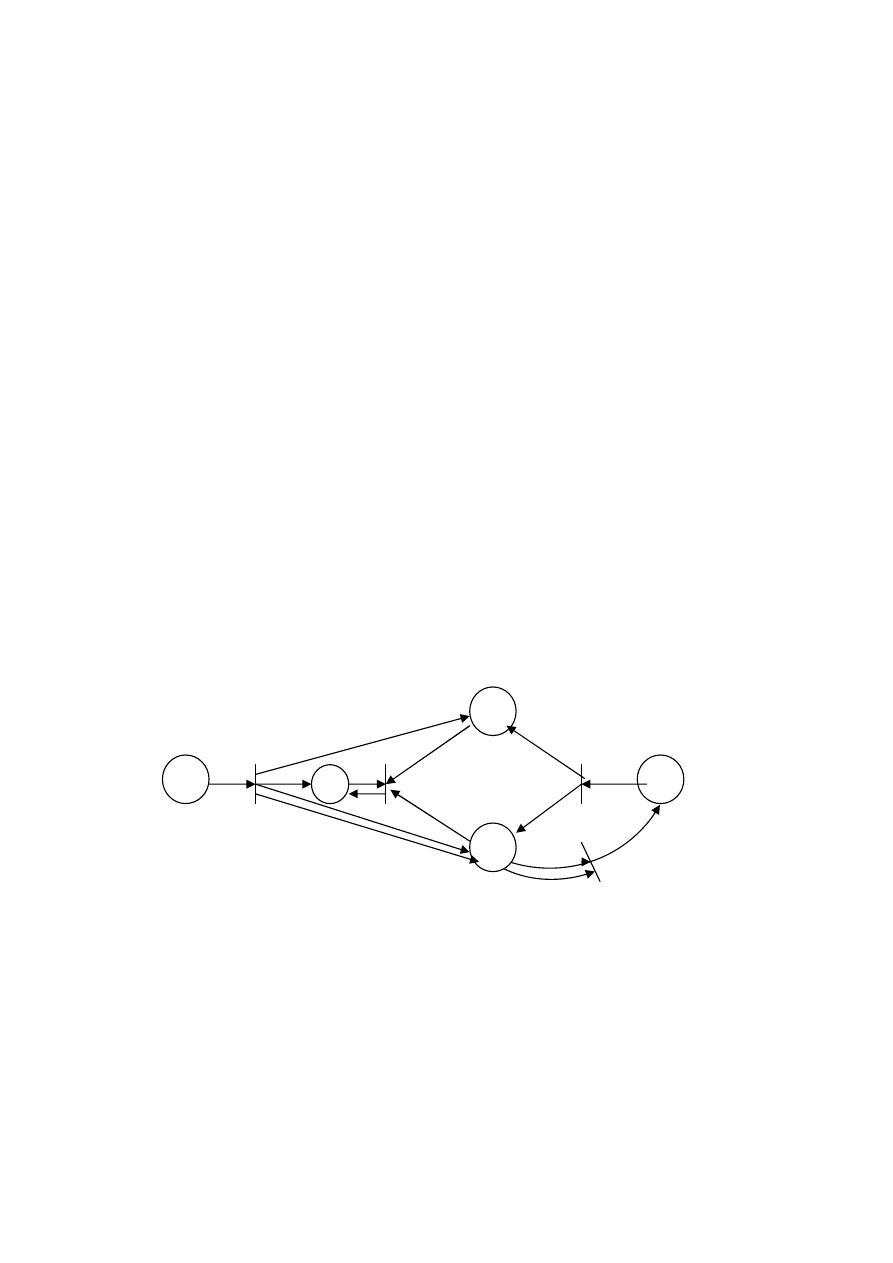
Рассмотрим
следующий
пример
.
Задана
сеть
Петри
(
рис
.
5.3).
Маркировка
сети
μ = (1, 0, 0, 2, 1).
При
такой
маркировке
разрешены
три
перехода
t
1
, t
3
, t
4
.
Переход
t
2
не
разрешен
,
по
-
скольку
две
из
трех
входных
позиций
не
содержит
ни
одной
Рисунок 9.35
фишки
.
Любой
из
разрешенных
переходов
может
быть
запущен
.
Запустим
переход
t
4
.
Фишка
удалится
из
р
5
,
одна
фишка
перемес
-
тится
в
позицию
р
3
и
одна
–
в
р
4
.
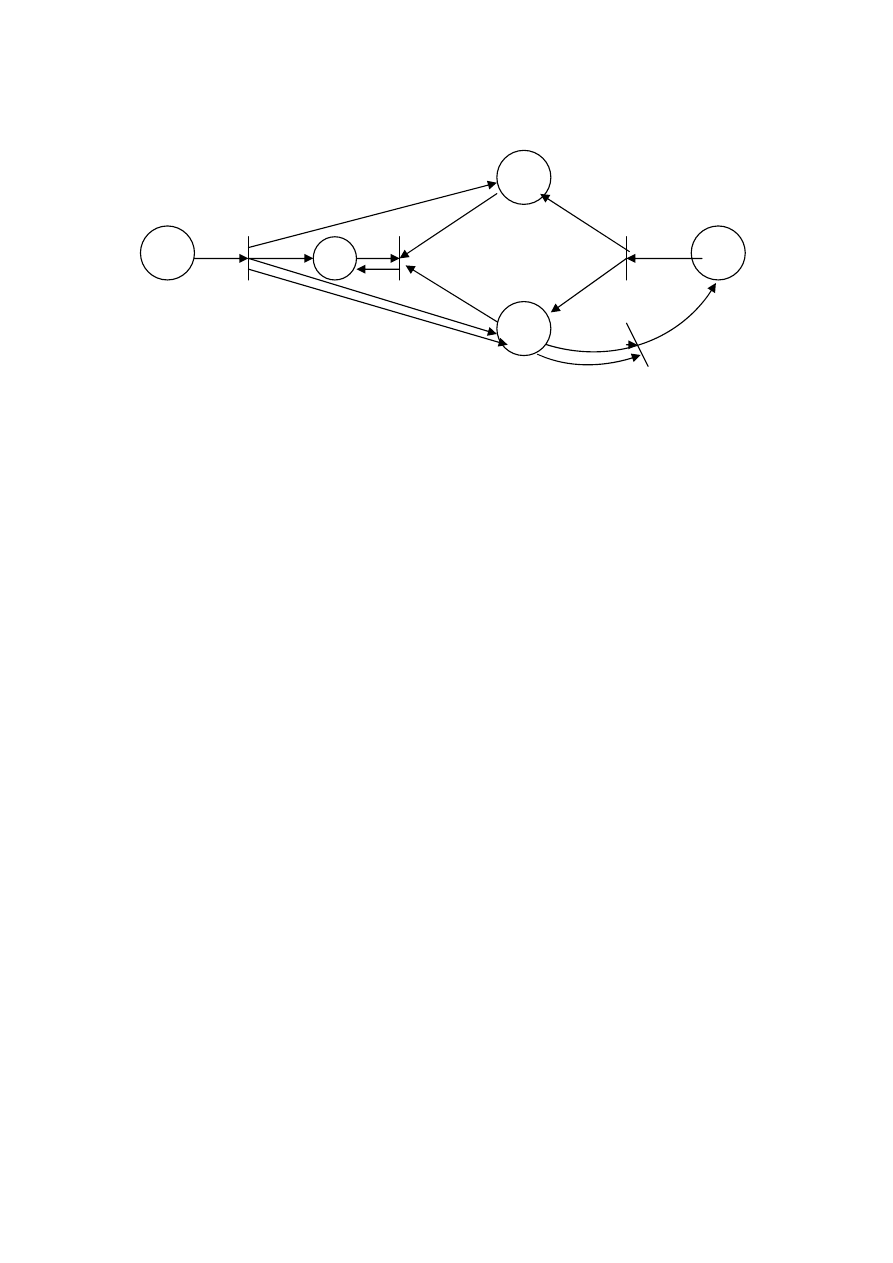
В
результате
сеть
Петри
будет
выглядеть
:
t
2
t
1
P
P
P
P
t
3
t
4
.
.
..
150
Рисунок 9.36
Пространство
состояний
сети
Петри
,
обладающей
конечным
числом
позиций
(n),
есть
множество
всех
маркировок
.
Измене
-
ние
в
состоянии
,
вызванное
запуском
очередного
перехода
,
осу
-
ществляется
с
помощью
функции
следующего
состояния
.
Функция
следующего
состояния
δ : N
n
x T
→ N
n
для
сети
Петри
С
с
маркировкой
μ
и
переходом
t
j
∈T
определена
тогда
и
только
тогда
,
когда
μ (p
i
)
≥ #(p
i
, I(t
j
)),
∀p
i
∈P.
В
случае
определения
функции
δ
осуществляется
отобра
-
жение
δ(μ, t
j
) =
μ’,
где
μ (p
i
) =
μ (p
i
) – (p
i
, I(t
j
)) + (p
i
, 0(t
j
)),
∀p
i
∈P.
При
выполнении
сети
Петри
получаются
две
последова
-
тельности
:
последовательность
маркировок
{
μ
0
,
μ
1
, …}
и
после
-
довательность
переходов
,
которые
были
запущены
{t
jo
, t
j1
,…},
связанные
отношением
:
δ(μ
k
, t
jk
) =
μ
k+1
, k = 0, 1, 2, …
Для
сети
Петри
С
= (P, T, I, 0)
с
маркировкой
μ
маркировка
μ’
называется
непосредственно
достижимой
из
μ,
если
∃
пере
-
ход
t
j
∈
Т
такой
,
что
δ(μ, t
j
) =
μ’.
Множеством
достижимости
R(C,
μ)
для
сети
Петри
с
марки
-
ровкой
μ
называется
наименьшая
последовательность
маркиро
-
вок
,
таких
что
:
P
3
P
2
t
2
t
1
P
4
P
5
P
1
t
3
t
4
.
.
. .
.