ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9326
Скачиваний: 24
141
В
общем
случае
для
определения
изоморфизма
необходимо
сделать
n!
сравнений
.
При
покрытии
функциональной
схемы
набором
стандарт
-
ных
модулей
или
при
решении
задачи
типизации
необходимо
ус
-
танавливать
изоморфизм
между
графом
G
и
какой
-
либо
частью
другого
графа
G’.
При
конструировании
схем
к
их
топологическому
чертежу
предъявляются
требования
получения
плоского
изображения
схем
.
Граф
G=(X, U)
называется
плоским,
если
он
расположен
на
плоскости
таким
образом
,
что
ребра
имеют
общие
точки
лишь
в
вершинах
.
Граф
,
изоморфный
плоскому
,
расположенный
на
плос
-
кости
и
имеющий
пересечения
ребер
,
называется
планарным.
Область
плоскости
,
ограниченная
ребрами
плоского
графа
,
внутри
которой
нет
ни
вершин
,
ни
ребер
,
называется
гранью.
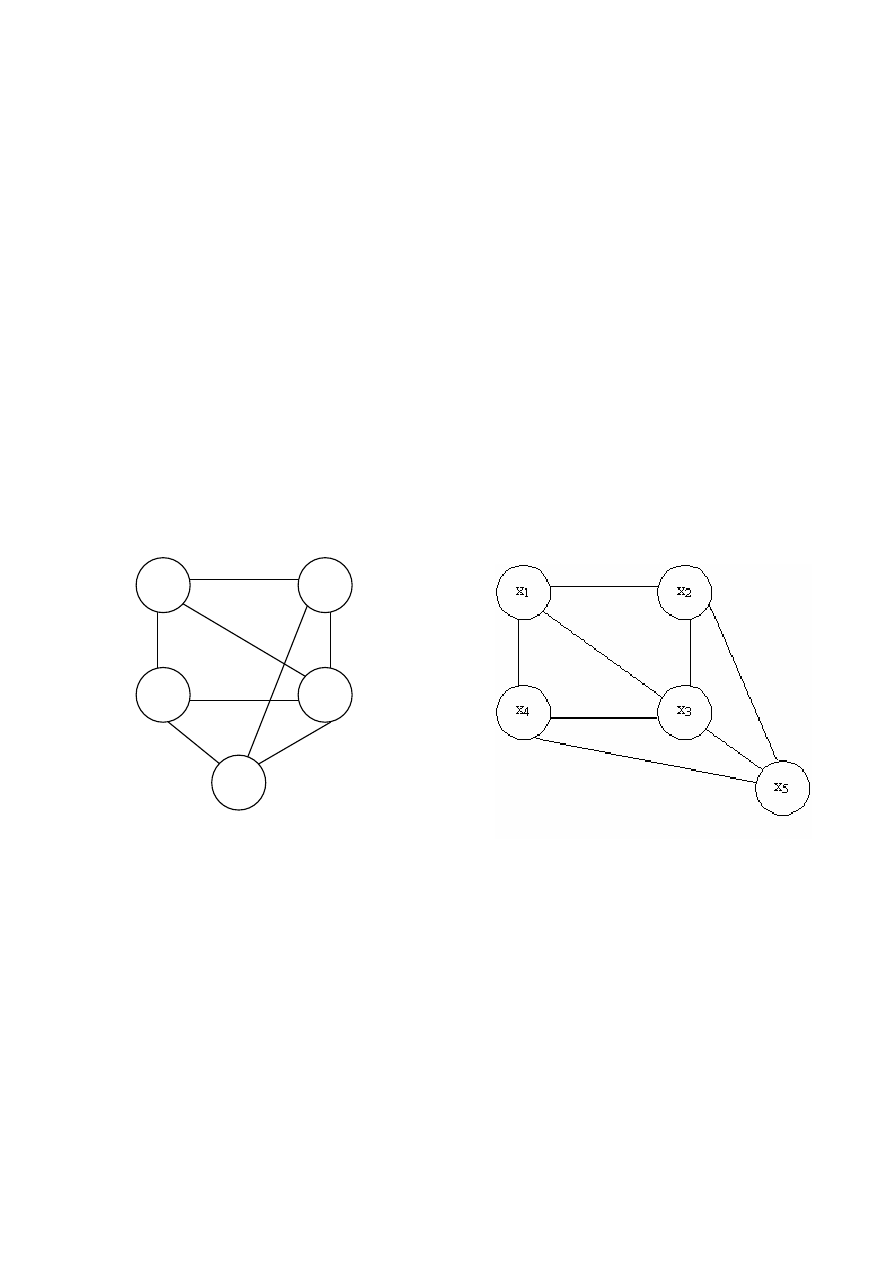
а) б)
Рисунок 9.30
− Планарный граф (а) и изоморфный ему плоский граф (б)
Ребра
грани
образуют
простой
цикл
.
Плоский
граф
имеет
всегда
одну
бесконечную
грань
,
не
ограниченную
ребрами
.
Су
-
ществует
формула
Эйлера
,
позволяющая
установить
связь
между
числом
вершин
и
числом
ребер
плоского
графа
:
n – m + f = 2,
где
f –
число
граней
плоского
графа
.
Определить
планарность
можно
с
помощью
различных
кри
-
териев
.
х
5
х
1
х
4
х
3
х
2

142
Пусть
задан
граф
G=(X, U).
Подразбиением
ребра
u
k
= (x
i
, x
j
)
называют
замену
его
двумя
ребрами
u
р1
= (x
i
, x
р
)
и
u
р2
= (x
р
, x
j
)
с
введением
новой
вершины
x
р
.
Два
графа
называют
гомеоморф
-
ными
,
если
они
обладают
изоморфными
подразбиениями
.
Теорема (Понтрягина-Куратовского).
Граф
планарен
то
-
гда
и
только
тогда
,
когда
он
не
содержит
подграфов
,
гомеоморф
-
ных
полному
графу
К
5
и
полному
двудольному
графу
К
3,3
.
Граф
планарен
тогда
и
только
тогда
,
когда
планарны
все
его
связные
компоненты
.
Распространенная
методика
определения
планарности
за
-
ключается
в
нахождении
в
графе
G
максимального
цикла
С
,
лучше
Гамильтонова
,
и
размещении
его
на
плоскости
в
виде
замкнутой
самопересекающейся
кривой
.
Далее
в
оставшейся
час
-
ти
определяют
пересекающиеся
по
ребрам
пути
и
предпринима
-
ют
попытки
разместить
каждый
из
путей
либо
внутри
С
,
либо
полностью
вне
С
.
Если
таким
образом
размещается
весь
граф
,
следовательно
,
он
планарен
,
в
противном
случае
–
не
планарен
.
Заметим
,
что
если
граф
связный
и
плоский
,
то
и
двойствен
-
ный
ему
граф
G
s
также
будет
плоским
и
связным
.
9.9
Орграфы
Орграф
G=(X,
U
)
будем
обозначать
D=(X, U)
и
называть
графом
.
Матрицей
смежности
графа
D
называется
матрица
R(D) =
=||r
ij
||
nxn
,
причем
1,
если
<xi, xj> –
дуга
D;
r
ij
=
0,
в
противном
случае
.
Так
как
r
ij
≠r
ji
,
то
матрица
не
симметрична
относительно
главной
диагонали
.
Дуга
u
i
= <x
i
, x
j
>.
Считается
положительно
инцидентной
ее
конечной
вершине
x
j
.
Число
дуг
,
положительно
инцидентных
вер
-
шине
x
j
,
называется
полустепенью захода
и
обозначается
ς
+
(x
j
).
Число
дуг
,
отрицательно
инцидентных
x
j
,
т
.
е
.
выходящих
из
x
j
,
на
-
зывается
полустепенью
исхода
и
обозначается
через
ς
–
(x
j
).
143
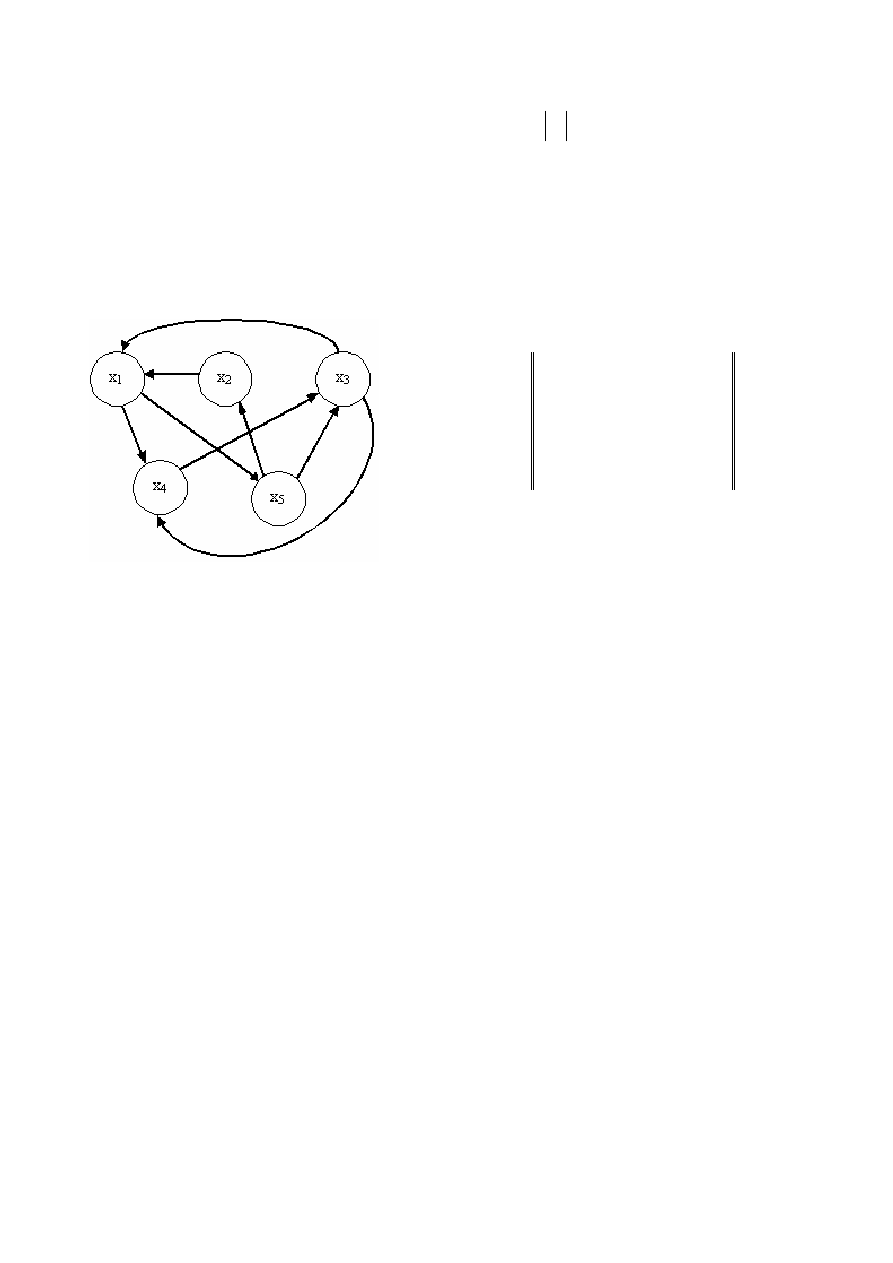
Из
матрицы
R(D) (
рис
. 9.31)
видно
,
что
суммы
элементов
по
строкам
равны
полустепеням
захода
вершин
D,
а
сумма
элемен
-
тов
по
столбцам
–
полустепеням
исхода
.
R(D) =
Рисунок 9.31
− Орграф и матрица смежности
Элементы
матрицы
инциденций
принимают
значения
0, +1,
–1.
Элемент
равен
нулю
,
если
вершина
не
инцидентна
дуге
, +1,
если
дуга
ориентирована
от
вершины
, +1,
если
дуга
ориентирова
-
на
к
вершине
.
Для
графа
D
на
рис
. 31
матрица
инциденций
имеет
вид
:
U
1
U
2
U
3
U
4
U
5
U
6
U
7
U
8
x
1
–1
–1
1 1 0 0 0 0
x
2
0 1 0 0 0 0 0 –1
x
3
1 0 0 0 –1
–1
1 0
x
4
0 0 0 –1
1 0 –1
0
x
5
0 0 –1
0 0 1 0 1
Маршрутом
графа
D
считается
чередующаяся
последова
-
тельность
вершин
и
дуг
(
х
0
, u
1
, x
1
, u
2
,…,u
n
, x
n
)
в
котором
каждая
дуга
u
i
есть
кортеж
u = <x
i
, x
j
>.
Маршрут
,
в
котором
все
вершины
различны
,
называется
путем.
Замкнутый
маршрут
,
у
которого
все
вершины
различны
,
за
исключением
первой
и
последней
,
на
-
зывается
контуром.
1 2 3 4 5
1 0 0 0 1 0
2 1 0 0 0 0
3 1 0 0 1 1
4 0 0 1 0 0
5 0 1 1 0 0
.
(
)
(
)
U
x
x
j
X
x
j
X
x
j
j
=
=
∑
∑
∈
−
∈
+
ρ
ρ

144
Если
существует
путь
из
вершины
x
i
в
вершину
x
j
,
то
гово
-
рят
,
что
x
j
достижима
из
x
i
.
Граф
D
называют
сильносвязным,
ес
-
ли
любые
две
его
вершины
взаимнодостижимы
.
Граф
G,
полученный
из
графа
D
заменой
каждой
дуги
u
i
=
=<x
i
, x
j
>
на
соответствующее
ребро
u
i
= (x
k
, x
l
),
т
.
е
.
устранением
стрелок
,
называется
основанием D.
Два
орграфа
называются
изоморфными,
если
можно
уста
-
новить
изоморфизм
между
их
основаниями
при
сохранении
по
-
рядка
стрелок
на
каждой
дуге
.
Неорграф
G
называется
ориентируемым,
если
каждое
его
ребро
можно
ориентировать
так
,
что
полученный
граф
будет
сильно
связным
.
Такой
процесс
называется
заданием
ориентации
графа
G.
Очевидно
,
что
произвольный
эйлеров
граф
может
быть
ориентируемым
,
так
как
достаточно
пройти
по
любой
эйлеровой
цепи
,
ориентируя
ребра
в
направлении
движения
.
Граф
D
называется
эйлеровым
,
если
в
нем
существует
замк
-
нутая
цепь
,
содержащая
каждую
его
дугу
.
Необходимым
услови
-
ем
существования
эйлерова
орграфа
является
его
сильная
связ
-
ность
.
Связный
граф
D = (X, U)
является
эйлеровым
,
когда
∀x
i
∈
Х
(
ς
+
(x
i
) =
ς
–
(x
i
)).
Орграф
называется
гамильтоновым
,
если
в
нем
существует
контур
,
содержащий
каждую
вершину
орграфа
.
Теорема.
Пусть
D –
сильно
связный
граф
.
Если
для
∀x
i
∈
Х
(
ς
+
(x
i
)
≥ n/2 n ς
–
(x
i
)
≥ n/2),
то
D –
гамильтонов
граф
.
Метод
Мальгранжа
разбиения
графа
D
на
максимально
связные
подграфы
.
Определим
прямое
и
обратное
транзитивные
замыкания
.
Прямым
транзитивным
замыканием
Г
+
х
i
называют
подмножест
-
во
вершин
X’
⊆X,
в
которые
можно
попасть
из
вершины
х
i
по
не
-
которому
пути
.
Здесь
Г
+2
х
i
=
Г
+
{
Г
+
х
i
},
Г
+3
х
i
=
Г
+
{
Г
+
{
Г
+
х
i
}},…
Об
-
ратным
транзитивным
замыканием
называют
подмножество
вершин
,
из
которых
можно
попасть
в
х
i
по
некоторому
пути
.
Обозначается
Г
–
х
i
.
Определим
обратное
и
прямое
транзитивное
замыкание
для
вершины
х
7
.
Г
+
х
7
= {x
7
,x
4
,x
6
},
Г
+2
x
7
=
Г
+
{
Г
+
x
7
} =
Г
+
{x
7
,x
4
,x
6
} =
={x
7
,x
4
,x
6
,x
2
,x
5
},
Г
+3
x
7
=
Г
+
{
Г
+2
x
7
} = {x
7
,x
6
,x
4
,x
5
,x
1
,x
2
,x
3
};
145
Г
–
x
7
= {x
7
, x
2
};
Г
–2
x
7
= {x
7
,x
2
,x
4
}.
Г
+
x
7
={x
7
}
∪
Г
+
x
7
∪
Г
+2
x
7
∪
Г
+3
x
7
={x
1
, x
2
, x
3
, x
4
, x
5
, x
6
, x
7
}.
Г
–
x
7
={x
7
}
∪
Г
–
x
7
∪
Г
–2
x
7
= {x
2
, x
4
, x
7
}.
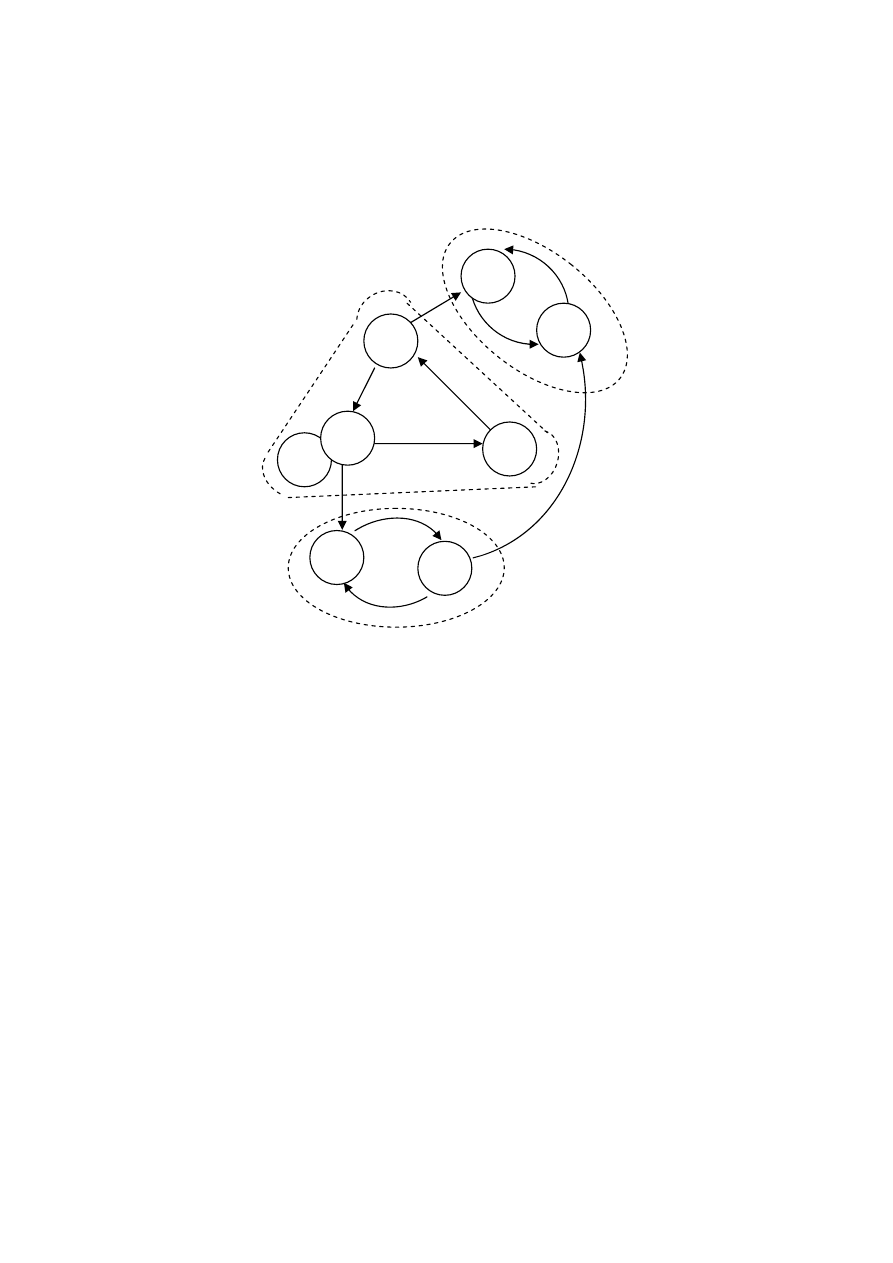
Рисунок 9.32
− Разложение графа на максимально связные графы
Основная
идея
алгоритма
заключается
в
следующем
.
Выби
-
рается
произвольная
вершина
x
i
∈X
графа
D
и
для
нее
определя
-
ется
Г
+
x
i
,
Г
–
x
i
и
С
(x
i
) =
Г
+
x
i
∩
Г
–
;
далее
выбирается
вершина
x
j
∉C(x
i
),
и
процесс
продолжается
аналогично
,
пока
возможно
.
В
результате
работы
алгоритма
получим
разбиение
графа
(
рис
. 32)
на
три
части
(
указаны
пунктиром
).
9.10
Сети
Петри
Сеть
Петри
в
графическом
представлении
является
дву
-
дольным
ориентированным
мультиграфом
.
Математически
сеть
Петри
основывается
на
понятии
ком
-
плекта
.
Комплект
,
как
и
множество
,
это
набор
элементов
из
некото
-
рой
области
Х
и
допускающий
присутствие
одного
и
того
же
х
2
х
7
х
4
х
1
х
3
х
6
х
5