ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9322
Скачиваний: 24
151
1)
μ ∈ R(C, μ);
2)
если
μ’∈ R(C, μ)
и
μ’’ = δ(μ, t
j
),
для
t
j
∈
Т
,
μ’’ ∈ R(C, μ).
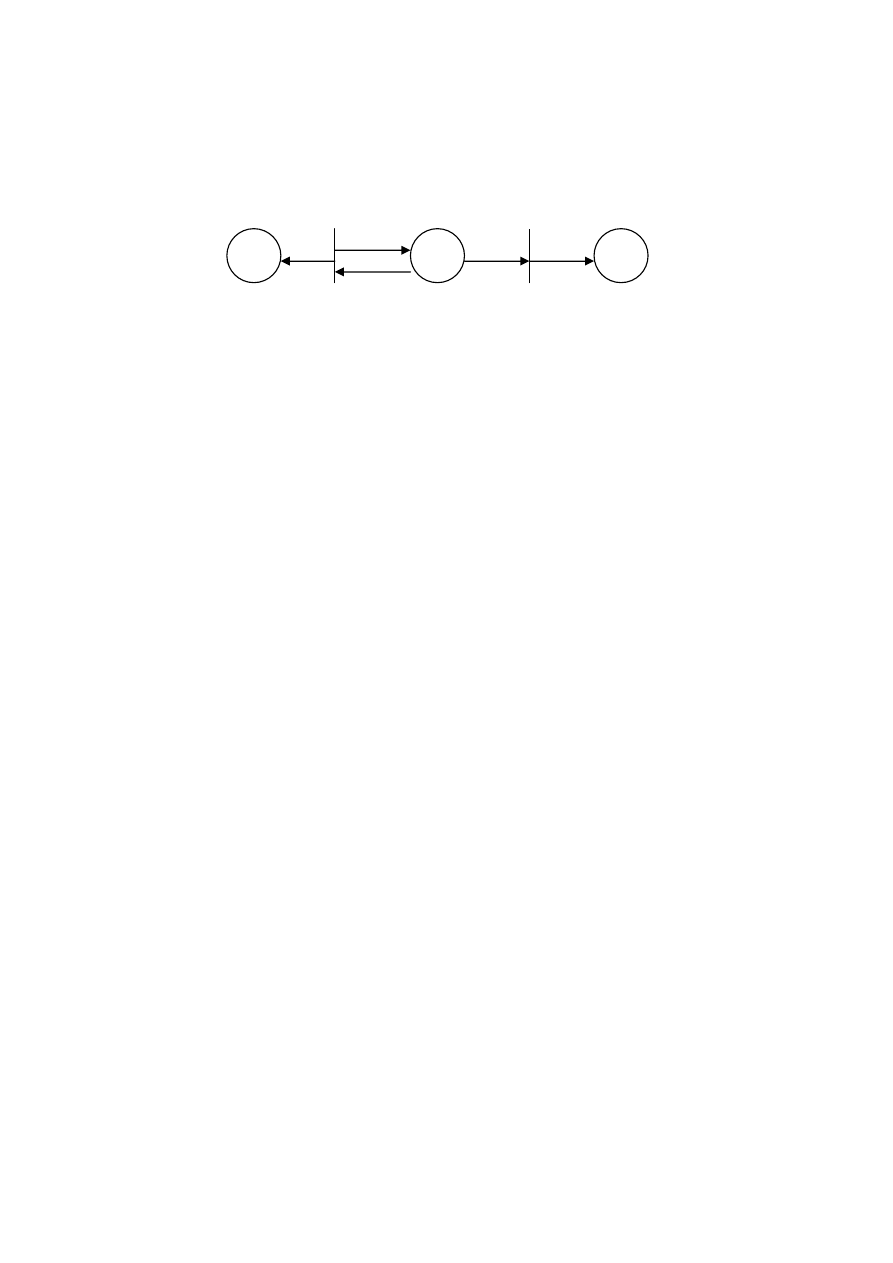
Приведем
в
качестве
примера
следующую
сеть
Петри
.
Рисунок 9.37
Для
этой
сети
с
начальной
маркировкой
μ = (1, 0, 0).
Непосредственно
достижимым
являются
две
маркировки
:
μ
1
= (0, 1, 0)
и
μ
2
= (1, 0, 1);
из
μ
1
нельзя
достичь
ни
одной
маркировки
.
Из
μ
2
можно
получить
(0, 1, 1)
и
(1, 0, 2).
Продолжая
процесс
,
можно
получить
(1, 0, n)
и
(0, 1, n), n
≤ 0.
P
2
P
3
P
1
t
1
t
2

152
КОНТРОЛЬНАЯ
РАБОТА
№
1 (
ВАРИАНТЫ
ЗАДАНИЙ
)
В
контрольную
работу
№
1
входят
соответствующие
номера
заданий
из
разделов
: «
Множества
», «
Графы
».
Множества
Вариант №1
1.
Укажите
все
элементы
множества
X={x
∈ A | x <10
и
A –
множество
простых
чисел
}.
2.
Сколько
элементов
в
следующих
множествах
: {d, f, u, df,
ff}, {1, 3, 4, 11,34}, {e, 4, ju, 7, 6}, {1, 11, 111,1}, {a, d, b, a, f, r,}?
3.
Дано
множество
А
={a,b,c,f,h}.
Укажите
верные
записи
:
1) a
∈A, 2) c ⊂ A, 3) ∅∈ A, 4){a,b,h}∈ A, 5){f,h}⊆A.
4.
Дайте
полное
определение
операции
объединения
.
5.
Укажите
верные
утверждения
А
⊕
В
⊕
С
=(
А
⊕
В
)
⊕
С
,
А
⊕
В
⊕
Т
=
А
⊕
В
,
А
⊕
Т
⊕
Т
=
А
⊕
Т
.
Вариант №2
1.
Сколько
элементов
в
следующих
множествах
: {x| x
≥ 1
и
x
≤ 4}, {rt, y, rt, tr,tt }, {2,4,6, 1+1,1+3}, { ←, ↑, ↓, →, →→, ←,
↓↑}?
2.
Дано
универсальное
множество
T = {0, 1, 2, 3, 4, 5, 6, 7, 8,
9}
и
множества
А
,
В
,
С
.
А
={1, 2, 3, 4, 7}, E= {3, 5, 4, 6}, C= {7, 4,
6, 8}.
Проиллюстрировать
графически
: (
Ā
∪
Ē
)
∩C.
3.
Дано
множество
А
={a,b,c,f,h}.
Укажите
верные
записи
:
1)
∅⊂ A, 2) {a,b,c,f,h}⊆A, 3) {a}⊂{a,b}, 4) A⊆ {a,b,c,f,h}.
4.
Дайте
определение
множества
.
5.
Упростить
А
∩¬
В
∪
А
∩¬
В
∩
С
∪
А
,
А
∩
В
∩¬
С
∪
А
∩
В
∩
С
∪
А
∩
С
.
Вариант №3
1.
Укажите
все
элементы
множества
X={x | x –
название
ме
-
сяца
,
начинающееся
с
буквы
м
}.
2.
Сколько
элементов
в
следующих
множествах
: {a, b, c,
ac}, {1,r,6,6r,11}, {
ℵ, ℜ, ℘, ℑ, ℜ, ℜℵ}, {
А
,
В
,
Р
,
О
,
Е
,
НЕ
}?

153
3.
Дано
множество
А
={a,b,c,f,h}.
Укажите
верные
записи
:
1) {c}
∈{a,c,f}, 2) ∅⊂ A, 3) {a,c}⊂ {b,c,f}, 4) ∅∈ {a,c,h}.
4.
Дайте
определение
операции
объединения
.
5.
Чему
равны
выражения
,
если
А
=
В
=
С
=
Д
=
Т
А
∩
В
∩
Ē
∪
Ē
∩
В
;
А
∩¬
В
∪
С
∪
Е
.
Вариант №4
1.
Укажите
все
элементы
множества
X={x | x=2n, n –
нату
-
ральное
число
и
n<5}.
2.
Дано
универсальное
множество
T = {0, 1, 2, 3, 4, 5, 6, 7, 8,
9}
и
два
подмножества
R={2}
и
Q = {2, 3, 8, 6}.
Изобразите
эти
множества
при
помощи
диаграмм
Эйлера
-
Венна
.
3.
Известно
,
что
A
⊂B
и
a
∈ A.
Какие
из
записей
верны
:
1) a
⊂A, 2){a}⊂B, 3)a∉B, 4){a}⊂ A.
4.
Дайте
полное
определение
операции
дополнения
.
5.
Упростить
,
если
А
⊂
В
,
В
=
С
¬(
А
∪
В
∩¬
С
)
¬(
А
∪¬(¬
В
∩
С
)).
Вариант №5
1.
Укажите
все
элементы
множества
X={x |x=2n, n
−
неотри
-
цательное
целое
число
и
n<5}.
2.
Дано
универсальное
множество
T = {0, 1, 2, 3, 4, 5, 6, 7, 8,
9}
и
два
подмножества
R={2}
и
Q = {2, 3, 8, 6}.
Укажите
элемен
-
ты
,
не
входящие
в
множество
Q.
3.
Даны
три
множества
A,B,C.
И
a
∈ A.
Укажите
верные
ут
-
верждения
. 1) a
⊂ B, 2) a∈A∪B, 3) a∈A∩C, 4) {a}∈A∪B∪C.
4.
Введите
понятие
универсального
множества
.
5.
Упростить
,
если
С
=
Т
и
D = 0, (A
∪B)∩(C∪D); ¬A ∩¬B
∩C∪B∩C∩D.
Вариант №6
1.
Укажите
все
элементы
множества
X={x |x=2n+2, n –
нату
-
ральное
число
и
n<5}.
2.
Дано
универсальное
множество
T = {0, 1, 2, 3, 4, 5, 6, 7, 8,
9}
и
два
подмножества
R={2, 3}
и
Q = {2, 7, 4, 8, 6}.
Изобразите
эти
множества
при
помощи
диаграмм
Эйлера
-
Венна
.

154
3.
Даны
три
множества
A,B,C.
И
a
∈ A.
Укажите
верные
ут
-
верждения
:
1) {a}
⊆ A,
2) {a}
⊂ A∪B. 3) {a}⊂A∩B. 4) a ∉ B.
4.
Чему
равно
число
всевозможных
подмножеств
любого
конечного
множества
,
содержащего
N
элементов
?
5.
Упростить
,
если
C =T; D=0, (¬A
∪B∪)∩(C∪D);
A
∩C∪¬B∩C∩A∩D.
Вариант №7
1.
Укажите
все
элементы
множества
X={x |x=2(n+1), n –
на
-
туральное
число
и
n
≤ 3}.
2.
Дано
универсальное
множество
T = {0, 2, 3, 4, 5, 6, 7, 8,
9}
и
два
подмножества
R={2, 3}
и
Q = {2, 7, 4, 8, 6}.
Укажите
эле
-
менты
,
не
входящие
в
множество
Q.
3.
Чему
равно
:1) A
∩A= 2) A∩T= 3) A∩∅=
4.
Определите
отношение
включения
.
5.
Упростить
выражение
¬A
∩(B∪C∪D)∩B∩C,
(A
∪B∪C)∩(¬B∪D),
если
C = T, D=0
Вариант №8
1.
Укажите
все
элементы
множества
X={x |x –
целое
число
и
|x|
≤ 2}.
2.
Универсальное
множество
T
представляет
собой
все
глас
-
ные
буквы
русского
алфавита
.
Множество
N = {
а
,
е
,
ы
,
и
,
э
}.
М
=
={
у
,
е
,
а
,
ы
,}.
Перечислите
все
элементы
,
которые
останутся
в
множестве
Т
,
если
из
него
удалить
все
элементы
,
не
входящие
в
множества
М
и
N.
3.
Чему
равно
:1) A
∪ A= , 2) A∪T = , 3) A∪∅=
4.
Дайте
определение
конечного
множества
.
5.
Упростить
A
∩B∩C∩D, ¬A∩¬B∪¬C∩¬D,
если
С
⊂ D,
A
⊂B
Вариант №9
1.
Укажите
все
элементы
множества
X={x |x =3n, n –
целое
число
и
|n|<3}.

155
2.
Универсальное
множество
T
представляет
собой
все
глас
-
ные
буквы
русского
алфавита
.
Множество
N = {
а
,
е
,
ы
,
и
,
э
}.
М
=
={
у
,
е
,
а
,
ы
,}.
Укажите
буквы
,
не
входящие
ни
в
множество
М
,
ни
в
множество
N.
3.
Чему
равно
1) A
∪
Ā
= 2) A
∩
Ā
=
4.
Дайте
определение
подмножества
.
5.
Упростить
(A
∪B)∩(C∪D), A∩¬B∪C∩¬D,
если
С
⊂ D,
A
⊂B
Вариант №10
1.
Дано
универсальное
множество
T = {0, 1, 2, 3, 4, 5, 6, 7, 8,
9}
и
множества
А
,
В
,
С
.
А
={1, 2, 3, 4, 7}, B= {3, 5, 4, 6}, C= {7, 4, 6, 8}.
Перечислите
элементы
множества
М
= {x| x
∉A
и
x
∈ T}.
2.
Приведите
законы
де
Моргана
.
3.
Укажите
верные
выражения
: (A
∪B)∩(A∪C)=A∪(B∩C),
(B
∪C)∩A=A∩B∪A∩C, (A∩B)=(B∩A).
4.
Дайте
определение
операции
объединения
.
5.
Упростить
¬(A
∪B)∩¬(C∪D), (
А
∪
В
∪C)∩(
В
∪
С
∪D),
ес
-
ли
С
⊂ D, A⊂B.
Вариант №11
1.
Укажите
все
элементы
множества
X = {x |x –
отличник
группы
577–1}.
2.
Дано
универсальное
множество
T = {0, 1, 2, 3, 4, 5, 6, 7, 8,
9}
и
множества
А
,
В
,
С
.
А
={1, 2, 3, 4, 7}, B= {3, 5, 4, 6}, C= {7, 4, 6, 8}.
Перечислите
элементы
множества
M = {x | x
∈ A∪B, x>4}.
3.
Приведите
законы
ассоциативности
.
4.
Укажите
верные
выражения
: (A
∪B)∩(A∪C)=A∩(B∪C),
A
∩B∪A∩C=A∪B∩C, A∩(B∪C)=A∪B∩C.
5.
Упростить
(¬A
∪B)∩(¬C∪D), A∩B∩
Ē
∪¬
А
∩
Е
,
если
С
=
=D =B=
Т
.
Вариант №12
1.
Укажите
все
элементы
множества
X ={x | x –
виды
хвой
-
ных
деревьев
,
растущих
в
Томском
районе
}.