ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6758
Скачиваний: 28
46
Таблица 2.2 – Матрица отклонений d(x
i
, x
j
)
Города
П Б Л Г М Н
Париж
0 2 1 1 2 2
Бордо
1 0 2 2 3 3
Лион
2 1 0 1 1 2
Гренобль
∞ ∞ ∞ 0 ∞ 1
Марсель
3 2 1 2 0 1
Ницца
∞ ∞ ∞ ∞ ∞ 0
Таблица 2.3 – Вектор отклоненностей d(x
i
)
Города
П
Б
Л
Г
М
Н
d(x
i
)
2 3 2
∞
3
∞
Для неориентированного графа, соответствующего графу, изо-
браженному на рис. 2.36, можно найти аналогичные характеристики,
но без учета ориентации дуг. При этом матрица d(x
i
, x
j
) оказывается
симметричной.
В связном неориентированном графе понятиям отклонения и
отклоненности соответствуют понятия: расстояние и удаленность.
Пусть G(X) – связный неориентированный граф. В соответст-
вии с определением связности для вершин x
i
и x
j
графа существует
элементарная цепь S(x
i
, x
j
) с концами x
i
и x
j
, причем l(S)
≥ 0.
Расстоянием d(x
i
, x
j
) между вершинами x
i
и x
j
называется дли-
на цепи S(x
i
, x
j
) наименьшей длины
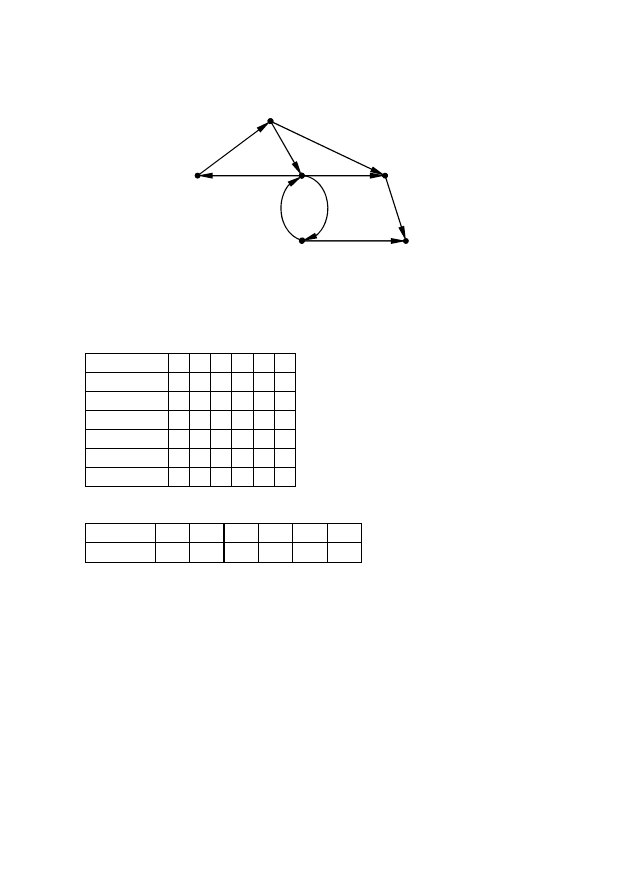
Париж
Гренобль
Ницца
Марсель
Лион
Бордо
Рис. 2.36 – Схема первой сети связи
для почтовых голубей

47
d(x
i
, x
j
) =
k
min
{l[S
k
(x
i
, x
j
)]}.
Удаленность вершины x
i
графа G(X) есть число
d(x
i
)=
X
x
j
∈
max
{d(x
i
, x
j
)}=
X
x
j
∈
max
{
min
k
{l[S
k
(x
i
, x
j
)]}}.
Центром графа называется вершина, в которой достигается
наименьшая из отклоненностей (удаленностей), если таковая являет-
ся конечным числом (Париж, Лион).
В графе может быть несколько центров, а может не быть ни
одного.
Периферийной вершиной графа называется вершина с наи-
большей отклоненностью или удаленностью (Гренобль, Ницца).
Радиусом
ρ(G) ориентированного графа называется отклонен-
ность его центра.
ρ(G) =
min ( )
x
X
i
i
d x
∈
=
m in m a x{m in{ [
(
,
)]}}
x
X
x
X
k
k
i
j
i
j
l S
x
x
∈
∈
.
В примере (рис.2.36)
ρ(G) = 2 (d(Париж) = d(Лион) = 2). Если в
графе нет центров, то полагают, что
ρ(G) = ∞. В неориентированном
графе
ρ(G) – удаленность центра.
Диаметром неориентированного графа называется удален-
ность периферийной вершины.
2.7
Определение
путей
и
кратчайших
путей
в
графах
2.7.1
Алгоритм
определения
пути
в
графе
Решение целого ряда практических задач, описываемых в тер-
минах графов, зависит от существования некоторой цепи, соеди-
няющей данную вершину с какой-либо другой. Например, в качест-
ве вершин графа можно рассматривать исходные позиции или со-
стояния некоторой головоломки или игры, а ребра будут указывать
возможные ходы из одной позиции в другую. Ребро будет неориен-
тированным или ориентированным в зависимости от того, обратим
переход или нет.
Граф G(X) с двумя отмеченными вершинами x
i
, x
j
называется
(x
i
, x
j
)-плоским, если граф G
′(X) = G(X) ∪ (x
i
, x
j
), полученный до-
бавлением к G(X) ребра (x
i
, x
j
), является плоским.
48
Рассмотрим алгоритм определения пути, ведущего из вершины
x
i
в x
j
плоского графа. Если x
i
не является вершиной никакого про-
стого цикла, то при определении алгоритма пути из x
i
в x
j
в графе
G(X) всегда выбирается самый левый или самый правый коридор
(ребро) (рис. 2.37).
Аналогичный алгоритм определения пути в прадереве предпо-
лагает следующие действия. Из корня идти по какой-либо ветви
насколько возможно далеко, затем возвратиться на какой-нибудь
перекресток и отправиться по новому направлению (еще не прой-
денному) и т.д. Искомый путь из x
i
в x
j
будет состоять из всех тех
ребер, которые в процессе поиска были пройдены по одному разу.
При определении пути в произвольном графе, не являющемся
прадеревом, приходим к предыдущему случаю следующим образом.
Если, пройдя по некоторому ребру g, попадаем на уже пройденный
ранее перекресток x, то ребро g «отсекается» от одной из своих кон-
x
i
x
8
x
3
x
7
x
5
x
6
x
11
x
12
x
14
x
15
x
13
x
16
x
19
x
j
x
17
x
18
x
20
x
i
x
9
x
10
x
i
x
1
x
2
x
4
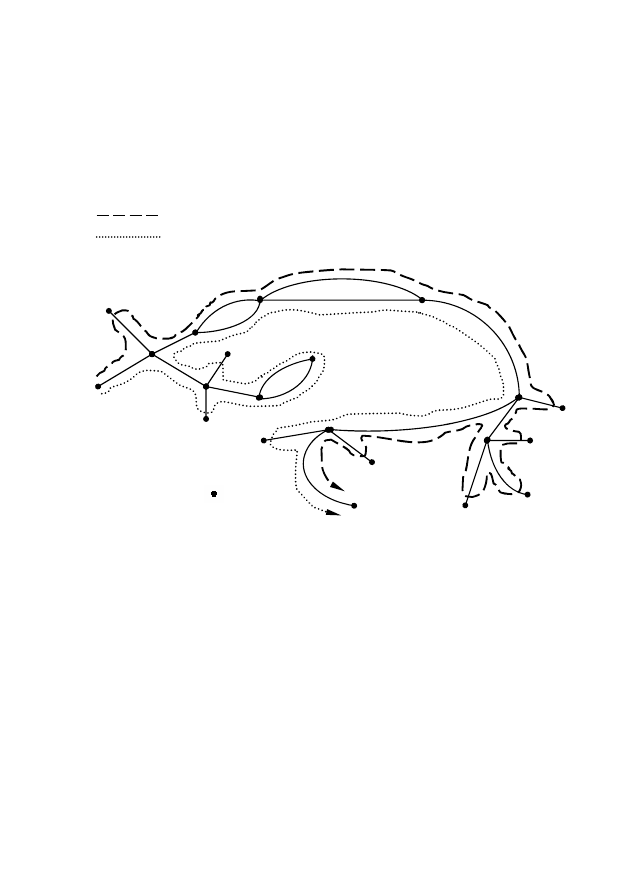
Рис. 2.37 – Определение пути в графе
путь при выборе левого коридора;
путь при выборе правого коридора.

49
цевых точек. После отсечения ребра, пройденные хотя бы один раз,
образуют прадерево.
При определении пути в графе с помощью алгоритма Тарри
необходимо в данном алгоритме пользоваться правилом:
•
не проходить дважды по одному ребру в одном и том же
направлении;
•
находясь в вершине x, не выбирать того ребра, которое при-
вело в данную вершину в первый раз (если есть возможность друго-
го выбора).
2.7.2
Алгоритм
определения
кратчайших
путей
в
графе
Эта задача имеет большое значение в практических примене-
ниях. К ней сводятся многие задачи выбора наиболее экономичного
(с точки зрения расстояния или стоимости) маршрута на имеющейся
карте дорог, наиболее экономичного способа перевода динамиче-
ской системы из одного состояния в другое и т.д. Существует много
математических способов решения, но часто методы, основанные на
теории графов, наименее трудоемки.
Рассмотрим задачу о кратчайшем пути. Пусть дан G(X), ду-
гам которого приписаны веса (расстояния, стоимости), задаваемые
матрицей
C
c
ij
=
. Задача о кратчайшем пути состоит в нахож-
дении кратчайшего пути от заданной начальной вершины s
∈ X до
заданной конечной вершины t
∈ X при условии, что такой путь су-
ществует. В общем случае возможно С
ij
> 0, С
ij
<0, С
ij
= 0. Единст-
венное ограничение состоит в том, чтобы в графе G(X) не было
циклов с отрицательным суммарным весом.
Приведем очень простой и эффективный алгоритм Дейкстры
решения этой задачи для случая С
ij
≥ 0 ∀ i, j. Алгоритм основан на
приписывании вершинам временных пометок, причем пометка вер-
шины дает верхнюю границу длины пути от s к этой вершине. Вели-
чины этих пометок постепенно уменьшаются с помощью некоторой
итерационной процедуры, и на каждом шаге итерации точно одна из
временных пометок становится постоянной. Это означает, что по-
метка уже не является верхней границей, а дает точную длину крат-
чайшего пути от s к рассматриваемой вершине.

50
Опишем этот алгоритм.
Пусть l(x
i
) – пометка вершины x
i
. Алгоритм Дейкстры состоит
из следующих этапов.
Присвоение начальных значений
Шаг 1. Положить l(s) = 0 и считать эту пометку постоянной.
Положить l(x
i
) =
∞ ∀ x
i
≠ s и считать эти пометки временными. По-
ложить p = s.
Обновление пометок
Шаг 2. Для всех x
i
∈ G(р), пометки которых являются времен-
ными, изменить пометки в соответствии с выражением
l(x
i
) = min [l(x
i
), l(p) + c(p, x
i
)]
(2)
Превращение пометки в постоянную
Шаг 3. Среди всех вершин с временными пометками найти та-
кую x
i
*
, для которой l(x
i
*
) = min[l(x
i
)]. Считать пометку вершины x
i
*
постоянной и положить p = x
i
*
.
Шаг 4, а (выполняется в случае, если требуется найти лишь
путь от s к t). Если p = t, то l(p) является длиной кратчайшего пути.
Останов. Если p
≠ t, перейти к шагу 2.
Шаг 4,б (Выполняется в случае, если требуется найти путь от s
ко всем остальным вершинам). Если все вершины отмечены как по-
стоянные, то эти отметки дают длины кратчайших путей. Останов.
Если некоторые пометки являются временными, перейти к шагу 2.
Проиллюстрируем работу алгоритма на примере графа, изо-
браженного на рис.2.38, матрица весов которого дана в табл.2.4.
Здесь каждое ребро рассматривается как пара противоположно ори-
ентированных дуг равного веса. Требуется найти все кратчайшие
пути от x
1
ко всем остальным вершинам. Постоянные пометки будем
обозначать знаком
+
.
Шаг 1. l(x
1
) = 0
+
, l(x
i
) =
∞ ∀ x
i
≠ x
1
, p = x
1
.
Первая итерация.
Шаг 2. G(p) = G(x
1
) = {x
2
, x
7
, x
8
, x
9
}.Все эти вершины имеют
временные пометки.