ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6754
Скачиваний: 28
36
x
2
x
1
x
3
x
4
x
5
x
2
x
1
x
3
x
4
x
5
x
2
x
1
x
3
x
4
1)
x
2
x
1
x
5
x
2
x
1
x
4
а)
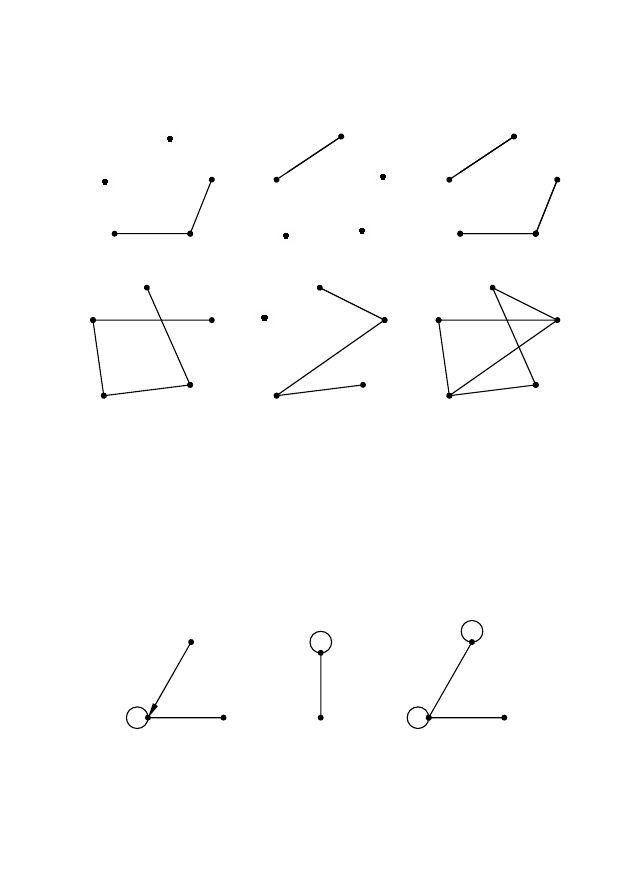
Рис. 2.24 – Примеры операции суммирования графов
G(X)=G
1
(X)
∪G
2
(X)
x
3
x
5
G
1
(X)
G
2
(X)
G(X)=G
1
(X)
∪G
2
(X)
x
1
x
2
x
5
x
4
x
3
x
1
x
2
x
5
x
4
x
3
x
1
x
2
x
5
x
4
G
1
(X)
G
2
(X)
G(X)=G
1
(X)
∪G
2
(X)
б)
G
1
(X)
G
2
(X)
x
4
x
3
x
3
Пример 1.
Рассмотрим случай, когда операция суммы графов применяется
к графам, определенным на различных множествах вершин. Тогда
суммой G(X) будет граф
n
G(X) = G
1
(X
1
)
∪ G
2
(X
2
)
∪ … ∪ G
n
(X
n
) =
∪ G
i
(X
i
),
i=1
для которого справедливо: Х = Х
1
∪ Х
2
∪ … ∪ Х
n
и
n
G(x
j
) = G
1
(x
j
)
∪ G
2
(x
j
)
∪ … ∪ G
n
(x
j
) =
∪ G
i
(x
j
), x
j
∈ X (рис. 2.25).
i=1
x
1
G
2
(X
2
)
G
1
(X
1
)
x
2
x
3
x
1
x
2
x
1
x
2
x
3
Рис. 2.25 – Суммирование графов с различными множествами
вершин
G
1
(X
1
)
∪G
2
(X
2
)
Пример 2.

37
Пересечение графов
Пусть даны два графа G
1
(X) и G
2
(X) на одном и том же множе-
стве вершин. Тогда пересечением графов G
1
(X) и G
2
(X) называется
граф G(X), состоящий из ребер, принадлежащих и G
1
(X) и G
2
(X), то
есть если (x
i
, x
j
)
∈ G
1
(X) и (x
i
, x
j
)
∈ G
2
(X), то (x
i
, x
j
)
∈ G(X).
Обозначение пересечения двух графов: G(X) = G
1
(X)
∩ G
2
(X).
Аналогично пересечение n графов G
i
(X) (i = 1, …, n) обознача-
ется как
n
G
i
(X) =
∩ G
i
(X) и определяет граф G(X), состоящий из ребер,
i=1
принадлежащих одновременно всем графам G
i
(X).
Для графов, используемых в примере 1 (рис. 2.24), имеем:
а) G
1
(X)
∩ G
2
(X) =
∅ (ноль - граф);
б) пересечение графов G
1
(X) и G
2
(X) изображено на рис. 2.26.
Для графов, определенных на различных множествах вершин
операция пересечения определяется следующим образом:
n
G(X) = G
1
(X
1
)
∩ G
2
(X
2
)
∩ … ∩ G
n
(X
n
) =
∩ G
i
(X
i
),
n
i=1
где Х = Х
1
∩ Х
2
∩ … ∩ Х
n
=
∩ X
i
i=1
n
и G(x
j
) = G
1
(x
j
)
∩ G
2
(x
j
)
∩ … ∩ G
n
(x
j
) =
∩ G
i
(x
j
),
x
j
∈ X.
i=1
Пересечение графов G
1
(X
1
) и G
2
(X
2
) примера 2 изображено на
рис. 2.27.
x
1
x
2
x
4
x
3
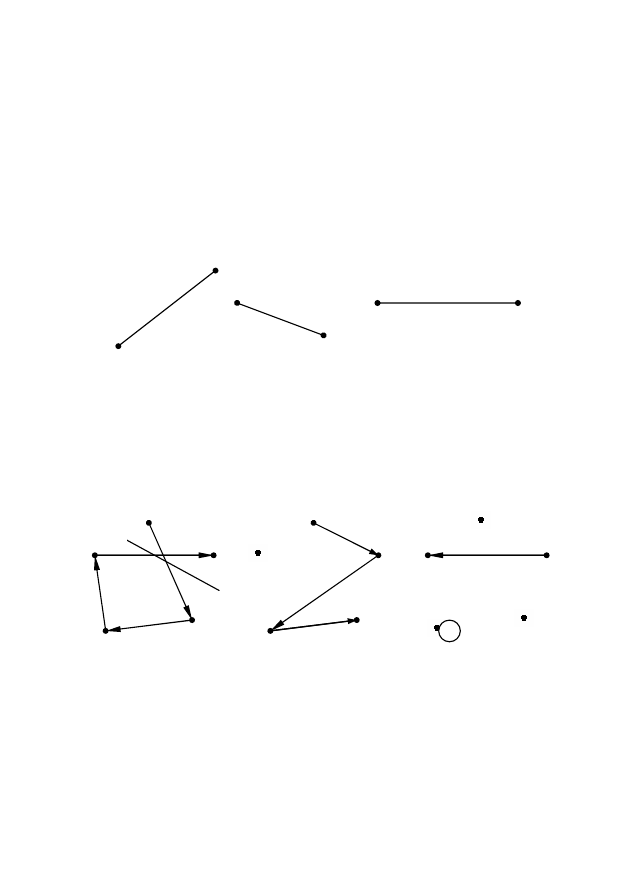
Рис. 2.26 – Пересечение
графов примера 1, б
x
1
x
2
Рис. 2.27 – Пересечение
графов примера 2
x
5
38
Композиция графов
Композицией (произведением) двух графов G
1
(X) и G
2
(X) с
одним и тем же множеством вершин Х является граф, у которого
множество вершин, смежных с вершиной x
i
, состоит из всех вершин,
достижимых из x
i
цепью длины два, первое ребро которой принад-
лежит G
2
(X), а второе – G
1
(X) (рис. 2.28). Здесь (x
i
, x
j
)
∈ G
2
(X),
(x
j
, x
k
)
∈ G
1
(X), (x
i
, x
k
)
∈ G
1
(G
2
(X)).
Композиция графов обозначается как G(X) = G
1
(G
2
(X)) (на
рис. 2.29 изображен пример композиции).
Пример 3.
Композицию графов, изображенных на рис. 2.29, иллюстрирует
табл.2.1.
x
i
x
j
x
j
x
k
x
i
x
k
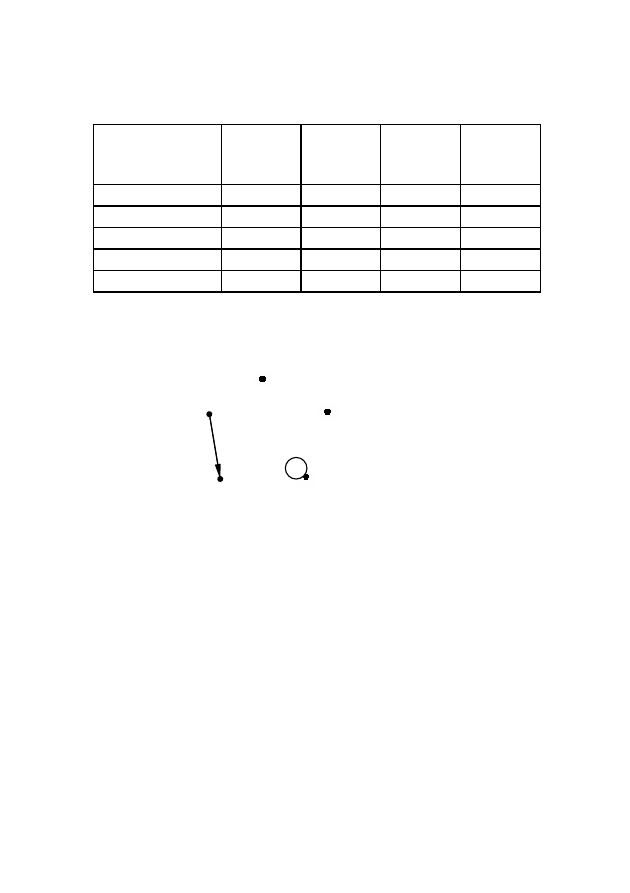
Рис. 2.28 – Иллюстрация операции композиции
x
5
x
1
x
2
x
4
x
3
G
1
(X)
Рис. 2.29 – Пример композиции графов
x
4
x
1
x
2
x
5
x
3
G
2
(X)
x
3
G
1
(G
2
(X))
x
1
x
2
x
5
x
4
39
Таблица 2.1 – Соответствие между вершинами графов (рис. 2.29)
Соответствие
Вер-
шина
(x
i
, x
j
)
∈
G
1
(X)
(x
i
, x
j
)
∈
G
2
(X)
(x
i
, x
j
)
∈
G
1
(G
2
(X))
(x
i
, x
j
)
∈
G
2
(G
1
(X))
x
1
(x
1
, x
4
) (x
1
, x
5
)
∅
∅
x
2
(x
2
, x
5
)
∅
∅
(x
2
,x
3
)
x
3
(x
3
, x
2
) (x
3
, x
4
) (x
3
, x
3
)
∅
x
4
(x
4
, x
3
)
∅
∅
(x
4
,x
4
)
x
5
∅
(x
5
, x
3
) (x
5
, x
2
)
∅
На основе таблицы можно построить G
1
(G
2
(X)) и G
2
(G
1
(X))
(рис. 2.30).
Транзитивное замыкание графов
Пусть имеется нетранзитивный ориентированный граф G(X).
Его можно сделать транзитивным, добавляя дуги с целью получения
замыкающей дуги (x
i
, x
k
) для каждой пары его последовательных дуг
(x
i
, x
j
) и (x
j
, x
k
). В этом случае говорят, что транзитивный граф
G
тр
(X) получен из нетранзитивного G(X) при помощи транзитивно-
го замыкания графа (аналогично транзитивному замыканию ото-
бражений)
G
тр
(X) = {x}
∪ G(x) ∪ G
2
(x)
∪ G
3
(x), …,
x
∈X.
G
2
(G
1
(X))
x
3
x
1
x
2
x
5
x
4
Рис.2.30 – Композиция G
2
(G
1
(X))
40
Пример 4.
Декартово произведение
Декартовым произведением двух графов G
1
(X
1
) и G
2
(X
2
) на-
зывается граф G(X) = G
1
(X
1
)
× G
2
(X
2
), определенный следующим
образом:
а) множество вершин Х является декартовым произведением
множеств Х
1
и Х
2
: Х = Х
1
× Х
2
= {(x
i1
, x
j2
) / x
i1
∈ X
1
, x
j2
∈X
2
};
б) множество вершин, смежных с вершиной (х
i1
, х
j2
) декартова
произведения двух графов, определяется как G(x
i1
, x
j2
) =
=G
1
(x
i1
)
×G
2
(x
j2
), т.е. как декартово произведение множеств вершин
графа G
1
(X
1
), смежных с х
i1
и графа G
2
(X
2
), смежных с x
j2
. Пример
приведен на рис. 2.32.
x
1
x
2
x
3
а)
x
1
x
2
x
3
x
4
G(X)
G(X)
б)
x
1
x
2
x
3
x
4
G
тр
(X)
x
1
x
2
x
3
G
тр
(X)
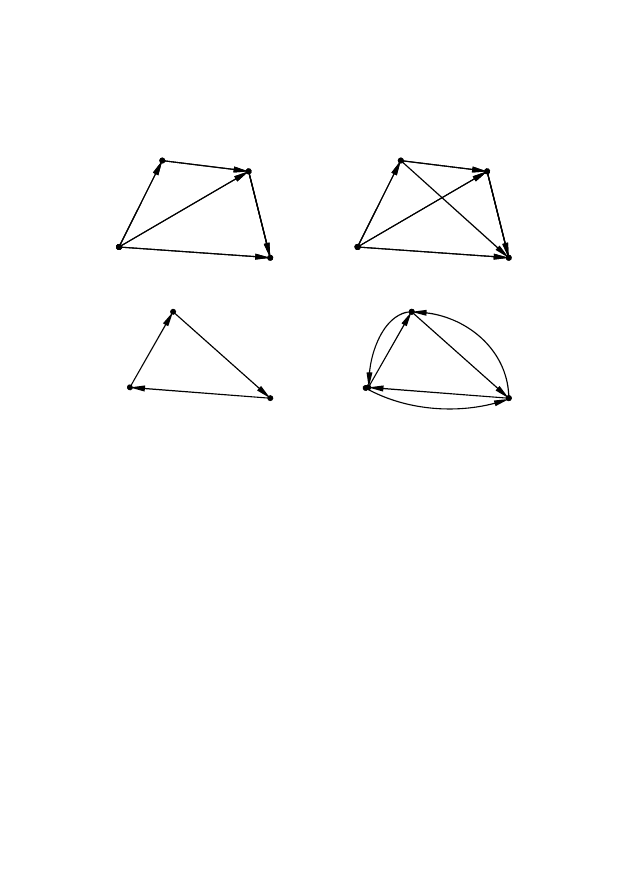
Рис. 2.31 – Примеры транзитивного замыкания графов