ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6755
Скачиваний: 28
41
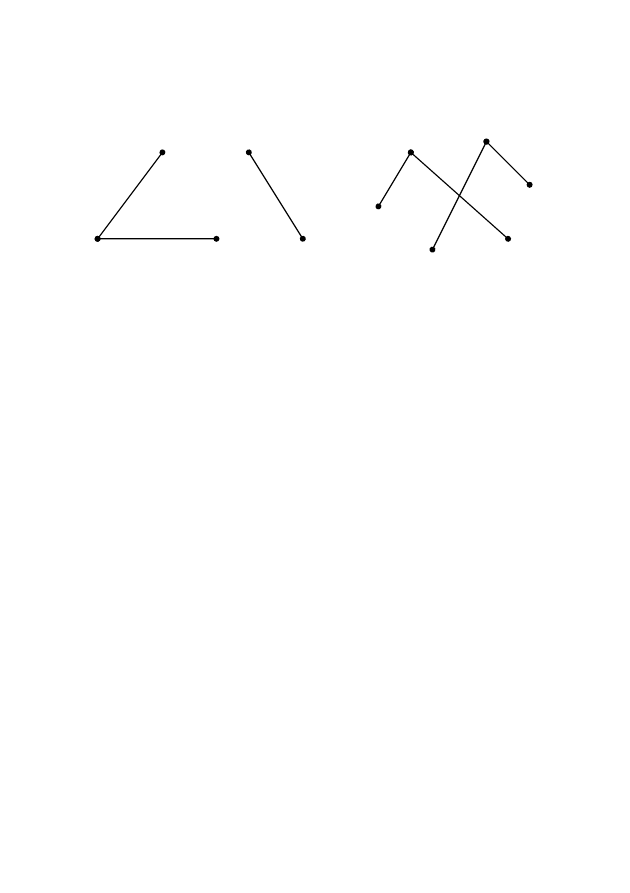
Пример 5.
Для примера 5
G(x
01
,x
02
)={(x
11
,x
12
), (x
21
,x
12
)},
G
1
(x
01
)={x
11
, x
21
},
G(x
01
, x
12
)={(x
11
, x
02
), (x
21
, x
02
)},
G
1
(x
11
)= x
01
,
G
2
(x
02
)=x
12
,
G(x
11
, x
02
)=(x
01
, x
12
),
G
1
(x
21
)= x
01
,
G
2
(x
12
)=x
02
,
G(x
11
, x
12
)=(x
01
, x
02
),
G(x
21
, x
02
)=(x
01
, x
12
),
G(x
21
, x
12
)=(x
01
, x
02
).
Пусть даны n графов G
1
(Х
1
), G
2
(Х
2
), ..., G
n
(Х
n
). тогда граф
G(Х)= G
1
(Х
1
)
× G
2
(Х
2
)
× ... × G
n
(Х
n
) называется декартовым
произведением указанных графов, если
а) Х = Х
1
× Х
2
× ... × Х
n
= {( x
1
, x
2
, ..., x
n
) / x
1
∈ X
1
, x
2
∈ X
2
, ... ,
x
n
∈ X
n
};
б) G(x
1
, x
2
, ... , x
n
) = G
1
(x
1
)
× G
2
(x
2
)
× ... × G
n
(x
n
) – декартово
произведение подмножеств вершин графов G
i
(x
i
) (i = 1, ..., n), смеж-
ных с вершинами x
1
, x
2
, ... , x
n
.
Декартова сумма графов
Декартовой суммой графов G
1
(Х
1
) и G
2
(Х
2
)
G(Х) = G
1
(Х
1
) + G
2
(Х
2
) называется граф, определенный следующим
образом:
а) множество вершин X является декартовым произведением
X
1
и X
2
, т.е. X = X
1
× X
2
= {(x
i1
, x
j2
) / x
i1
∈ X
1
, x
j2
∈ X
2
};
б) множество вершин, смежных с вершиной (x
i1
, x
j2
) определя-
ется как G(x
i1
, x
j2
) = [G
1
(x
i1
)
× {x
j2
}]
∪ [{x
i1
}
× G
2
(x
j2
)] (
× − операция
декартова произведения).
G
1
(X
1
)
x
G
2
(X
2
)
x
G
1
(X
1
)
× G
2
(X
2
)
(x
01
, x
02
)
(x
01
, x
12
)
(x
11
, x
02
)
(x
11
, x
12
)
(x
21
, x
02
)
(x
21
, x
12
)
x
11
x
01
x
21
x
02
x
12
Рис. 2.32 – Декартово произведение графов
42
Для примера 5
G(x
01
, x
02
) = {G
1
(x
01
)
× {x
02
}}
∪ {{x
01
}
× G
2
(x
02
)} =
= {(x
11
, x
02
), (x
21
, x
02
)}
∪ {(x
01
, x
12
)},
G(x
01
, x
12
) = {G
1
(x
01
)
× {x
12
}}
∪ {{x
01
}
× G
2
(x
12
)}=
= {(x
11
, x
12
),(x
21
, x
12
)}
∪ {(x
01
, x
02
)},
G(x
11
,x
02
) = {(x
01
, x
02
)}
∪ {(x
11
, x
12
)}, G(x
11
, x
12
) = {(x
01
, x
12
)}
∪ {(x
11
,
x
02
)},
G(x
21
,x
02
) = {(x
01
, x
02
)}
∪ {(x
21
, x
12
)}, G(x
21
, x
12
) = {(x
01
, x
12
)}
∪ {(x
21
,
x
02
)}.
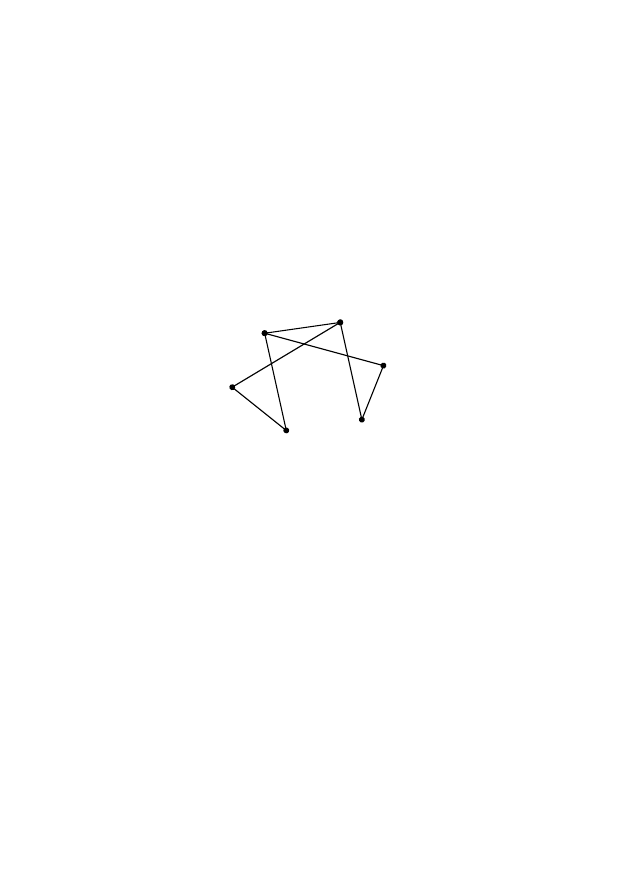
Соответствующий граф изображен на рис. 2.33.
Граф G(X) называется декартовой суммой n графов
G(X) = G
1
(X
1
) + G
2
(X
2
) + ... + G
n
(X
n
), если
а) X = X
1
× X
2
× ... × X
n
;
б) G(x
1
, x
2
, ... , x
n
) = [G
1
(x
1
)
× {x
2
}
× ... × {x
n
}]
∪ [{x
1
}
× G
2
(x
2
)
× ...
× {x
n
}]
∪ ... ∪ [{x
1
}
× {x
2
}
× ... × G
n
(x
n
)].
2.5
Степени
графов
2.5.1
Степени
неориентированных
графов
Пусть G(X) – неориентированный граф. Степенью m(x) графа
G(X) в вершине x называется число ребер, инцидентных вершине x.
Если все числа m(x) для x
∈ X конечны, то граф называется ло-
кально конечным. Петли можно считать одинарным или двойным
ребром в зависимости от конкретной задачи.
G(X) = G
1
(X
1
) + G
2
(X
2
)
(x
01
, x
02
)
(x
01
, x
12
)
(x
11
, x
02
)
(x
11
, x
12
)
(x
21
, x
02
)
(x
21
, x
12
)
Рис. 2.33 – Декартова сумма графов
43
Обозначим m(x
i
, x
j
) = m(x
j
, x
i
) – число ребер, соединяющих
вершины x
i
и x
j
. Если в графе G(X) нет кратных ребер, то
m(x
i
, x
j
) = 0 или m(x
i
, x
j
)=1.
Очевидно, что m(x
i
) =
∑
∈ X
x
j
i
j
x
x
m
)
,
(
.
Поскольку каждое ребро учитывается в двух вершинах x
i
и x
j
,
то общее число ребер m графа G(X)
∑ ∑
∑
∈
∈
∈
=
=
X
x
X
x
j
i
X
x
i
i
j
i
x
x
m
x
m
m
)
,
(
2
1
)
(
2
1
(1)
Это выражение справедливо и для графов с петлями, если пет-
лю считать двойным ребром.
Так как
∑
∈ X
x
i
j
x
m
)
(
– четное число, то можно сделать вы-
вод о том, что в конечном графе число вершин с нечетной степе-
нью четно.
Это следует из того, что если из суммы вычесть все слагаемые,
соответствующие вершинам с четной степенью, она останется чет-
ной.
Граф, степени всех вершин в котором равны, называется одно-
родным, т.е. m(x
i
) = m
n
∀ x
i
∈ X.
Конечные однородные графы могут быть представлены в виде
правильных многогранников (Платоновых тел): тетраэдра, куба,
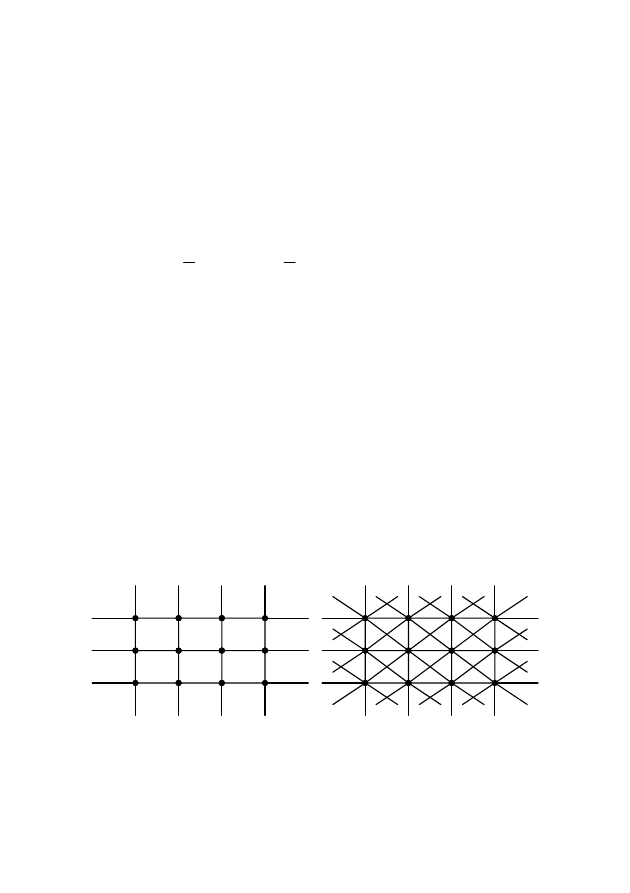
октаэдра, додекаэдра, икосаэдра и т.д. Примеры бесконечных одно-
родных графов изображены на рис. 2.34.
Рис. 2.34 – Бесконечные однородные графы

44
Из (1) следует, что в однородном графе степени m
n
число ребер
равно
m
m
n
n
=
×
1
2
, где n – число вершин.
2.5.2
Степени
ориентированных
графов
В ориентированном графе существуют такие понятия, как по-
лустепени исхода и захода.
Полустепенью исхода m
′(x) называется число дуг, выходящих
из вершины x. Полустепень захода m
″(x) – число дуг, входящих в
вершину x. Петли считают по одному разу в каждой из полустепе-
ней.
Аналогом кратности неориентированных ребер m(x
i
, x
j
) в ори-
ентированном графе являются две кратности: m
′(x
i
, x
j
) – число дуг,
направленных от x
i
к x
j
, и m
″(x
i
, x
j
) – число дуг, направленных от
x
j
к x
i
.
Таким образом, m
′(x
i
, x
j
) = m
″(x
j
, x
i
).
Число дуг, выходящих из вершины x
i
, определится суммой
∑
∑
∈
∈
′′
=
′
=
′
X
x
i
j
X
x
j
i
i
j
j
x
x
m
x
x
m
x
m
)
,
(
)
,
(
)
(
,
а число дуг, входящих в вершину x
i
, равно
∑
∑
∈
∈
′
=
′′
=
′′
X
x
i
j
X
x
j
i
i
j
j
x
x
m
x
x
m
x
m
)
,
(
)
,
(
)
(
.
Отсюда общее число дуг графа
∑∑
∑∑
∑
∈
∈
∈
∈
∈
′′
=
′
=
′
=
X
x
X
x
i
j
X
x
X
x
j
i
X
x
i
i
j
i
j
i
x
x
m
x
x
m
x
m
m
)
,
(
)
,
(
)
(
.
Если все полустепени m
′(x) и m″(x) равны для всех x ∈ X, то
ориентированный граф G(X) называется однородным графом сте-
пени m
n
.
Для такого графа m = m
n
× n, где n – число вершин графа G(X).
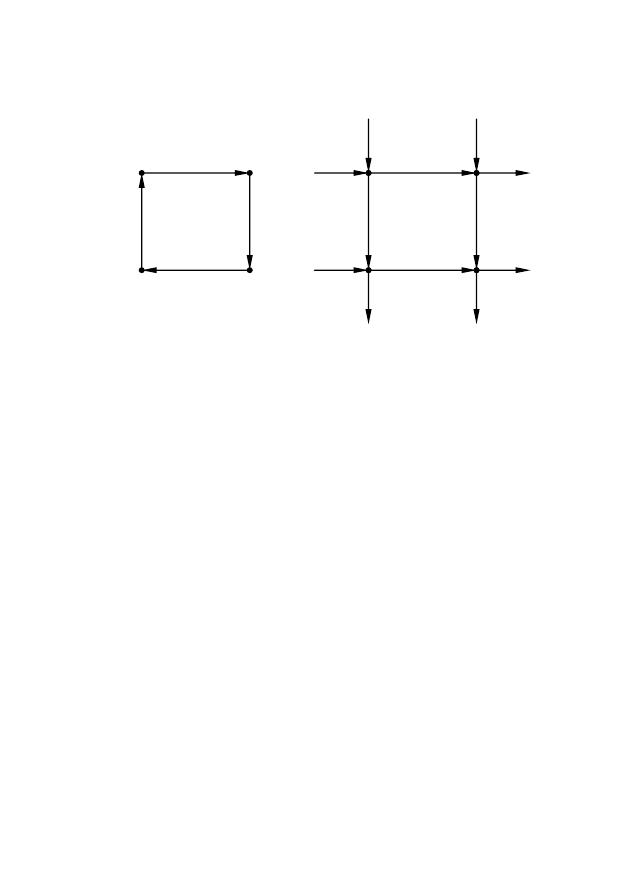
Примеры однородных ориентированных графов приведены на
рис.2.35.
45
2.6
Характеристики
расстояний
в
графах
Пусть G(X) – конечный или бесконечный ориентированный
граф. Отклонением d(x
i
, x
j
) его вершины x
i
от вершины x
j
называ-
ется длина кратчайшего пути из x
i
в x
j
: d(x
i
, x
j
) =
k
min
{l[S
k
(x
i
, x
j
)]}.
Отклонение d(x
i
, x
j
) удовлетворяет следующим аксиомам мет-
рического пространства:
1) d(x
i
, x
j
)
≥ 0;
2) d(x
i
, x
j
) = 0
⇔ x
i
= x
j
;
3) d(x
i
, x
j
) + d(x
j
, x
k
)
≥ d(x
i
, x
k
) – неравенство треугольника
и не удовлетворяет четвертой аксиоме, а именно:
4) d(x
i
, x
j
)
≠ d(x
j
, x
i
) так как граф ориентирован.
Необходимо отметить, что если x
j
∉ G(x
i
), то d(x
i
, x
j
) = ∞.
Отклоненностью вершины x
i
называется наибольшее из от-
клонений d(x
i
, x
j
) по всем x
j
:
d(x
i
) =
X
x
j
∈
max
{d(x
i
, x
j
)} =
X
x
j
∈
max
{
min
k
{l[S
k
(x
i
, x
j
)]}}.
В качестве примера рассмотрим схему первой (1870 г.) сети
связи для почтовых голубей. Граф, представляющий ее, изображен
на рис. 2.36, а матрица отклонений и вектор отклоненностей – в
табл. 2.2 и табл.2.3 соответственно.
x
1
x
2
x
3
x
0
Рис. 2.35 – Конечный и бесконечный однородные ориентированные
графы