ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6750
Скачиваний: 28
26
Частичный граф содержит часть ребер (дуг). Он также может
быть ориентированным или неориентированным в зависимости от
исходного.
Отметим, что ноль-граф графа G(X) считается частичным гра-
фом каждого графа. Все частичные графы H(X) для G(X) можно
получить, выбирая в качестве ребер H(X) всевозможные подмноже-
ства множества ребер графа G(X).
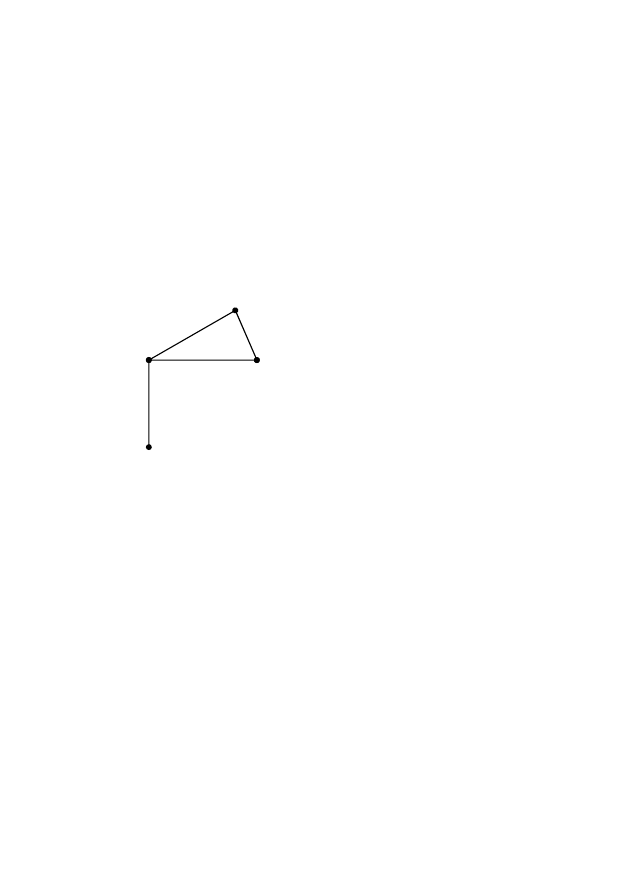
Подграфом G
A
(A) графа G(X), где A
⊂ X, называется граф,
вершинами которого являются элементы множества A
⊂ X, а ребра-
ми – все ребра из G, оба конца которых лежат в A (рис.2.9).
Таким образом, под-
граф содержит часть вер-
шин вместе с ребрами, со-
единяющими эти вершины.
Иначе, G
A
(A) – подграф
графа G(X), если A
⊂ X и
G
A
(x) = G(x)
∩ A. Если
A = X, то G
A
(A) = G(X).
Для единственной вершины
A={a} подграф G
A
(a) со-
стоит из петель в а. Под-
графом G
A
(A) графа G(X)
будет
ноль-граф,
если
A
⊂ X есть подмножество изолированных вершин графа G(X). Под-
граф будет ориентированным или неориентированным в зависимо-
сти от графа.
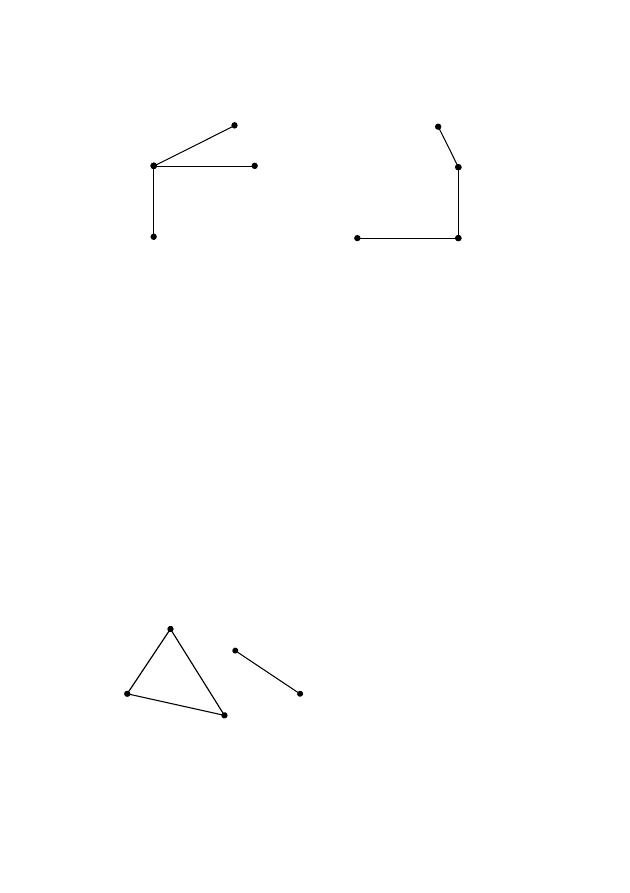
Частичным подграфом H
A
(A), A
⊂ X графа G(X) называется
подграф (рис.2.10), ребрами которого являются некоторые ребра из
G(X), оба конца которых лежат в A. Иначе, H
A
(A) – частичный под-
граф графа G(X), если A
⊂ X и H
A
(x)
⊂ G(x) ∩ A ∀ x∈X.
Дополнительным частичным графом H(A)
графа G(X) явля-
ется единственный граф, состоящий из ребер графа G(X), не при-
надлежащих некоторому частичному подграфу H
A
(A) графа G(X)
(рис.2.11).
x
2
x
3
x
1
x
0
Рис. 2.9 –
Подграф
G
A
(A) графа G(X)
27
x
2
x
3
x
1
x
0
Рис. 2.10 – Частичный подграф
H
A
(A) графа G(X)
x
2
x
3
x
4
x
0
Рис. 2.11 – Дополнительный
частичный граф H(A)
графа G(X)
Звездным графом, определяемым вершиной х, называется
граф, состоящий из всех ребер G(X), имеющих х концевой верши-
ной. Петли в х могут как включаться, так и не включаться в звезд-
ный граф.
2.1.6
Связность
в
графах
Рассмотрим вопрос о связности в графах. Пусть G(X) – неори-
ентированный граф. Две вершины х
i
, х
j
называется связными, если
существует цепь S с концами х
i
и х
j.
Если S проходит через некото-
рую вершину x
k
более одного раза, то можно удалить цикл в верши-
не x
k
из цепи S. Отсюда следует, что вершины, связанные цепью,
связаны элементарной цепью.
Неориентированный граф называется связным, если любая па-
ра его вершин связана. Отношение связности для вершин графа есть
отношение эквивалентности (x
i
∼ x
j
, x
j
∼ x
k
,
⇒ x
i
∼ x
k
).
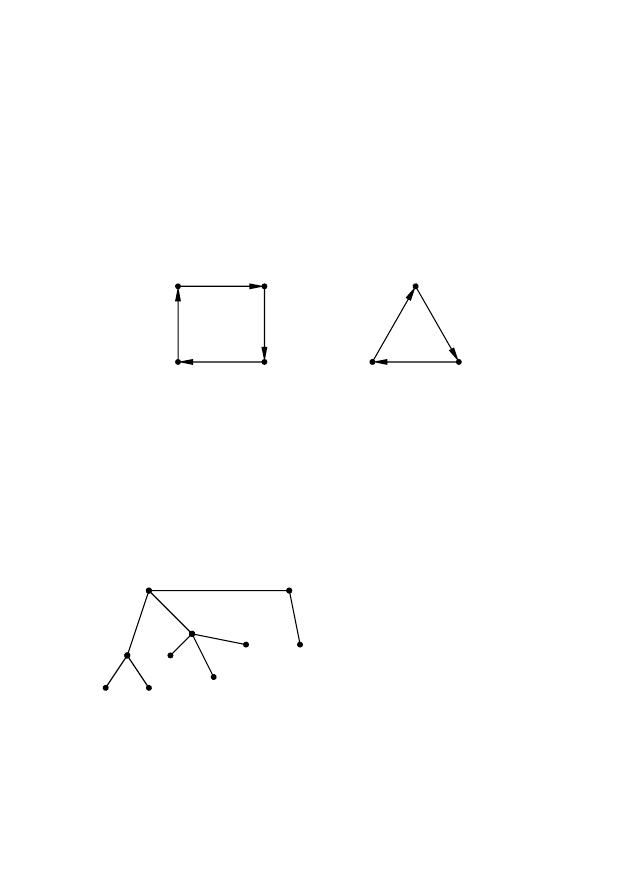
Компонентой связ-
ности неориентирован-
ного графа G(X) называ-
ется подграф H
A
(A) графа
G(X) с множеством вер-
шин A
⊂ X и множеством
ребер в G(X), инцидент-
ных только вершинам из
A, причем ни одна вер-
шина из x
i
∈ A не смежна
с вершинами из множест-
x
4
x
5
x
3
x
1
x
2
Рис. 2.12 – Граф с двумя
компонентами связности
28
ва X \ A (рис.2.12).
Ориентированный граф называется сильно связным, если для
любой пары вершин найдется путь, соединяющий их.
Компонентой сильной связности ориентированного графа
G(X) называется подграф H
A
(A) графа G(X) (подчиняющийся опре-
делению сильно связного графа) с множеством вершин A
⊂X и мно-
жеством дуг, имеющих начало и конец в A, причем ни одна из вер-
шин x
i
∈ A и x
j
∈ X \ A не смежны между собой (рис.2.13).
Очевидно, что ориентированный граф G(X) сильно связан то-
гда и только тогда, когда он имеет одну компоненту связности.
На практике широко используются такие виды графов, как де-
ревья и прадеревья.
Деревом называется конечный связный неориентированный
граф, состоящий по крайней мере из двух вершин и не содержащий
циклов. Такой граф не имеет петель и кратных ребер (рис.2.14).
Ветвями дерева назы-
ваются ребра графа, вхо-
дящие в дерево. Хордами
дерева называются ребра,
входящие в граф, дополни-
тельный к данному дереву.
Лагранжевым дере-
вом называется дерево, все
ветви которого имеют об-
щую вершину.
Лесом называется несвязный граф, каждая компонента связно-
сти которого является деревом.
x
1
x
6
x
7
x
5
x
4
x
3
x
2
Рис. 2.13 – Ориентированный граф с двумя
компонентами сильной связности
x
4
x
3
x
9
x
7
x
8
x
2
x
6
x
5
x
0
x
1
Рис. 2.14 – Дерево
29
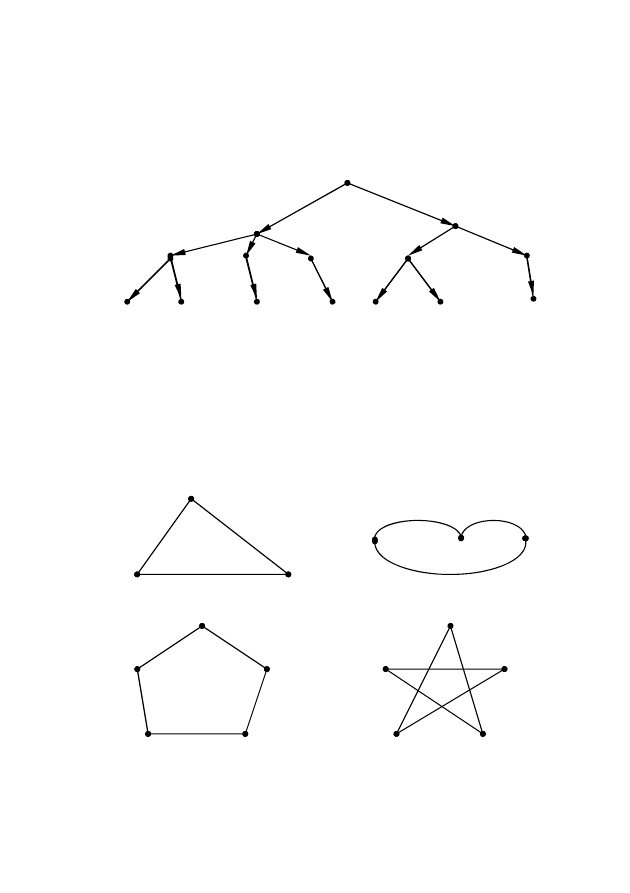
Прадеревом называется ориентированный граф G(X) с корнем
x
1
∈ X, если в каждую вершину x
i
≠ x
1
(x
i
∈ X) заходит ровно одна
дуга, в вершину x
1
не заходит ни одна дуга, граф G(Х) не содержит
контуров (рис.2.15).
2.1.7
Изоморфизм
.
Плоские
графы
В изображении графа имеется относительно большая свобода в
размещении вершин и в выборе формы соединяющих их ребер. По-
этому один и тот же граф может быть представлен (на плоскости)
по-разному (рис. 2.16).
Рис. 2.15 – Прадерево
x
3
x
2
x
1
x
3
x
1
x
2
G
1
(X
1
)
x
4
x
5
x
1
x
2
x
3
x
5
x
3
x
1
x
4
x
2
G
1
(X
1
)
G
2
(X
2
)
Рис. 2.16 – Примеры изоморфных графов
G
1
(Х
1
)
G
2
(Х
2
)
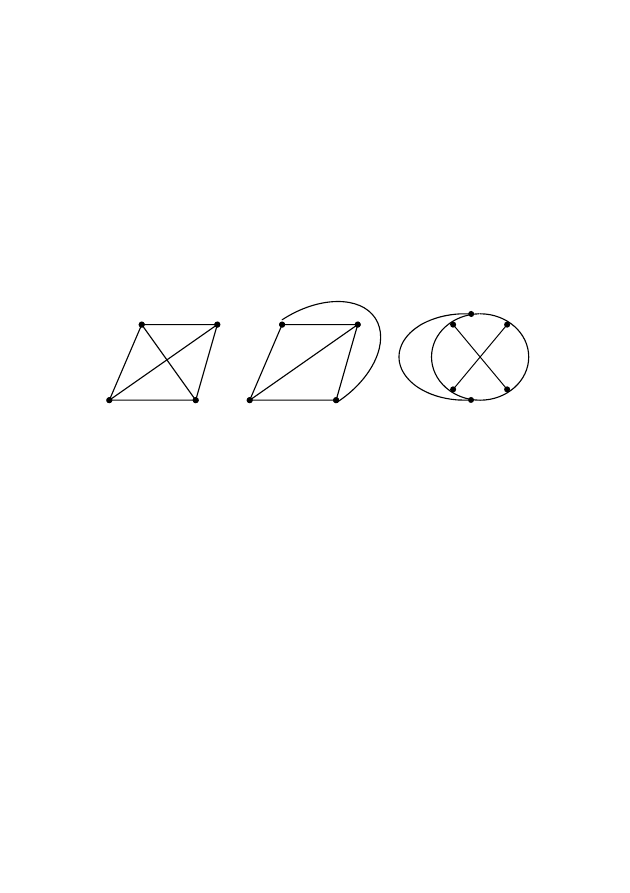
30
Графы G
1
(X
1
), G
2
(X
2
) называются изоморфными, если между
множествами их вершин существует взаимно однозначное соответ-
ствие, такое, что вершины соединены ребрами в одном из графов в
том и только том случае, когда соответствующие им вершины со-
единены в другом графе. Если ребра графов ориентированы, то их
направление в изоморфных графах также должно соответствовать
друг другу.
Граф G(X) называется плоским, если он может быть изобра-
жен на плоскости так, что все пересечения его ребер являются вер-
шинами графа G(X) (рис.2.17).
2.2
Отношения
на
множествах
и
графы
Каждый ориентированный граф G(X) определяет некоторое от-
ношение на множестве X своих вершин. Это отношение может быть
записано как x
i
G x
j
. Оно означает, что в графе есть дуга, идущая от
x
i
к x
j
.
Отношению со свойством рефлексивности (x R x) должна со-
ответствовать на графе петля в вершине. Если это отношение со-
блюдается во всех вершинах x
∈ X, то соответствующий граф G(X)
должен иметь петлю в каждой своей вершине. В случае антиреф-
лексивного отношения на множестве X, соответствующий граф ни
в одной из вершин не имеет петли.
Симметрическому отношению на множестве X соответствует
граф с неориентированными ребрами и наоборот граф с неориенти-
рованными ребрами определяет некоторое симметрическое отноше-
Рис. 2.17 – Примеры плоского (а) и неплоского (б) графов
x
4
x
1
x
2
x
4
x
1
x
2
x
3
а)
x
2
x
1
x
3
x
6
x
5
x
4
б)
x
3