ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6751
Скачиваний: 28
31
ние. В случае антисимметрического отношения на графе невоз-
можно присутствие двух дуг (x
i
, x
j
), (x
j
, x
i
) на графе, то есть сущест-
вование неориентированного ребра. Кроме того, на этих графах нет
петель, то есть соответствующее антисимметрическое отношение
антирефлексивно.
Отношение, обладающее свойством тождественности, соот-
ветствует графу с антисимметричным отношением на множестве
вершин (ориентированному графу) и добавлением петли в каждой
вершине. Этот граф не должен иметь контуров.
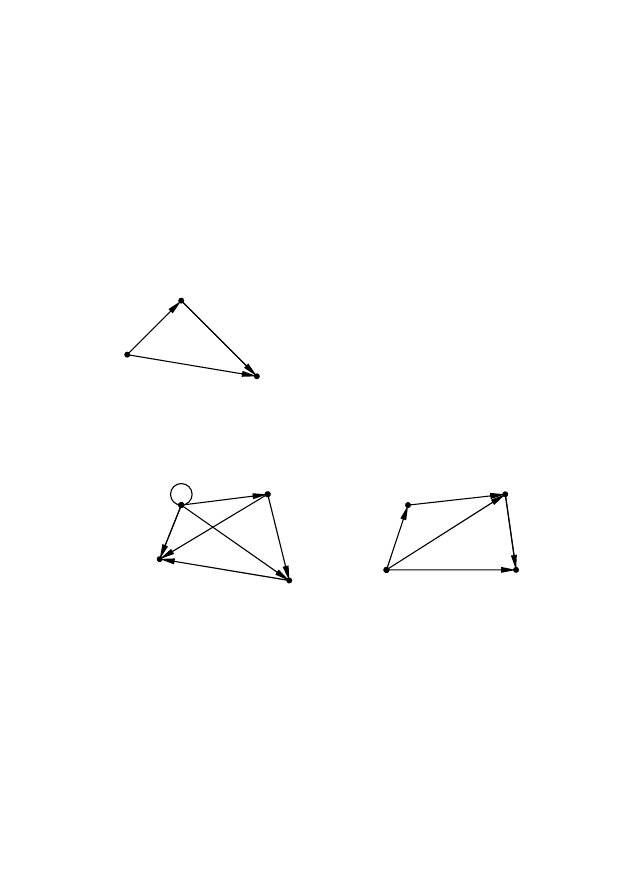
Граф,
соответствующий
транзитивному
отношению
(рис.2.18), обладает следующи-
ми свойствами: для любой пары
ориентированных ребер (дуг)
графа (x
i
, x
j
),(x
j
, x
k
) имеется за-
мыкающая дуга (x
i
, x
k
). Можно
сказать, что в графе, который
соответствует
транзитивному
отношению, для каждого пути
S(x
i
, x
k
) имеется дуга (x
i
, x
k
) (рис.2.19).
Отношение, обладающее свойством полноты, определено на
множестве вершин полного ориентированного графа.
Нулевое отношение определено на множестве вершин ноль-
графа.
Универсальное отношение определено на множестве вершин
полного неориентированного графа с петлями.
x
k
x
i
x
j
Рис. 2.18 – Свойство транзи-
тивности на графе
x
1
x
2
x
3
x
4
x
1
x
2
x
3
x
4
Рис. 2.19 – Примеры транзитивного (а) и нетранзитивного (б) графов
а)
б)
32
Дополнительное к R отношение
⎯R определено на множестве
вершин дополнительного G
k
(X)графа к графу G(X).
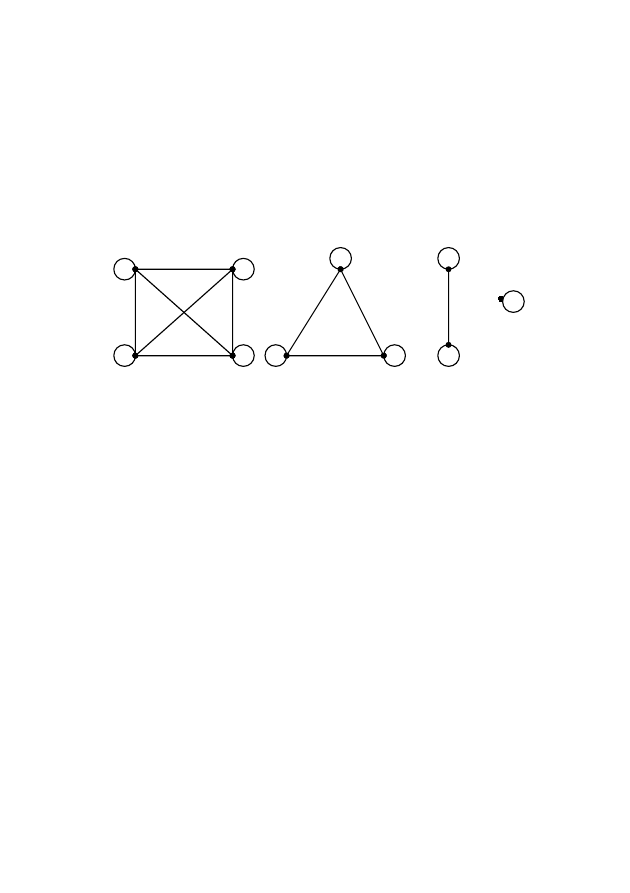
Графы, соответствующие отношению эквивалентности, пред-
ставляют собой совокупность компонент связности (для каждого
класса эквивалентности своя компонента) несвязного графа. Каждая
компонента несвязного графа должна быть полным неориентиро-
ванным графом с петлями (рис. 2.20).
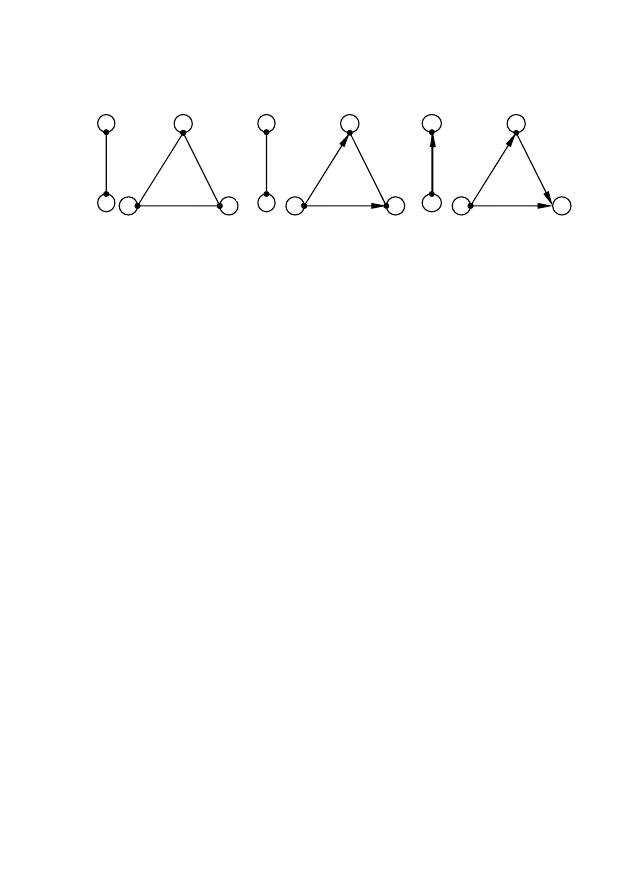
При рассмотрении отношения квазипорядка соответствующий
граф должен иметь петли в каждой вершине и может иметь неори-
ентированные и ориентированные ребра. В отличие от предыдущего
случая здесь не соблюдается свойство симметричности (рис. 2.21, а,
б, в).
Граф, на множестве вершин которого определено отношение
эквивалентности, одновременно является графом, на множестве
вершин которого определено отношение квазипорядка.
Граф, на множестве вершин которого определено отношение
порядка, является также графом, на множестве вершин которого
определено отношение квазипорядка. Этот граф:
•
имеет петли во всех вершинах;
•
для каждого пути S(x
i
, x
k
) должен иметь замыкающую дугу
(x
i
, x
k
);
•
не должен иметь контуров и все ребра должны быть ориен-
тированы (рис. 2.21, в).
x
4
x
1
x
2
x
3
x
10
x
5
x
7
x
6
x
8
x
9
Рис. 2.20 – Граф, соответствующий отношению эквивалентности
33
Граф, на множестве вершин которого определено отношение
строгого порядка, получается удалением всех петель в графе, на
множестве вершин которого определено отношение порядка.
Отношение полного порядка соответствует каждой компонен-
те связности графа, на множестве вершин которого определено от-
ношение порядка.
Если на графе G(X) определено одно из отношений эквива-
лентности, квазипорядка, порядка, строгого порядка, полного по-
рядка, нулевое, универсальное, дополнительное, то данное отноше-
ние сохраняется и на графе G
-1
(X).
2.3
Матрицы
смежности
и
инциденций
графа
Если в графе G(X) через a
ij
обозначить число дуг, идущих из x
i
в x
j
, то матрица || a
ij
|| с n строками и n столбцами называется матри-
цей смежности вершин графа. Здесь a
ij
– элемент, стоящий на пе-
ресечении i-й строки и j-го столбца, a
i
– i-я вектор-строка, a
j
– j-й
вектор-столбец.
Наличие нулевого элемента на главной диагонали означает от-
сутствие петли в соответствующей вершине.
Матрица A
T
соответствует графу G
-1
(X).Матрица А является
симметрической тогда и только тогда, когда граф G(X) – симметри-
ческий. Матрица А антисимметрична тогда и только тогда, когда
граф G(X) – антисимметрический. Матрица А полна тогда и только
тогда, когда граф G(X) – полный (a
ij
+ a
ji
≥ 1).
x
2
x
1
x
3
x
5
x
4
Рис. 2.21 – Примеры графов, на которых определено отношение
квазипорядка
а)
x
2
x
1
x
3
x
5
x
4
б)
x
2
x
1
x
3
x
5
x
4
в)
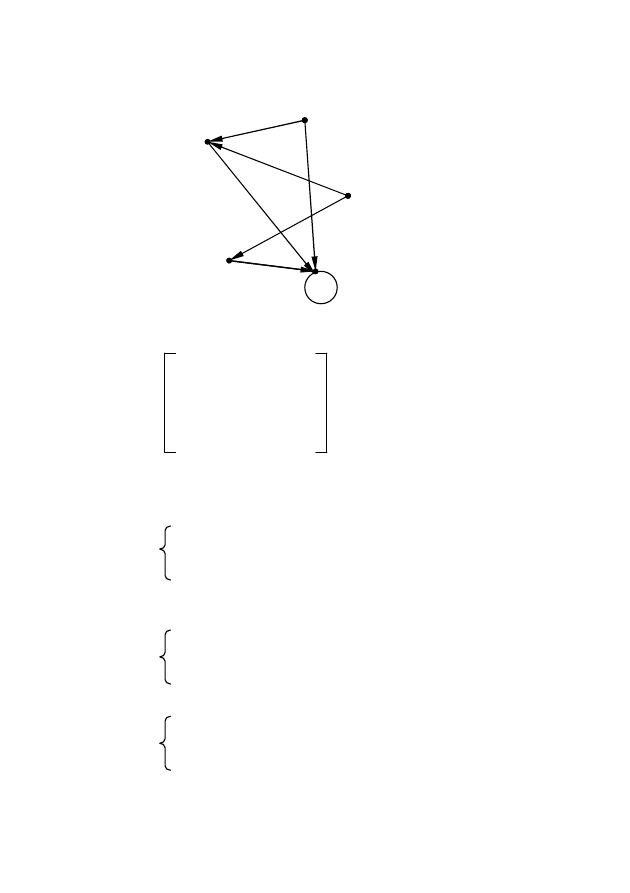
34
x
1
x
2
x
3
x
4
x
5
x
1
0 1 0 0 1
x
2
0 0 0 0 1
А = x
3
0 1 0 1 0
x
4
0 0 0 0 1
x
5
0 0 0 0 1
Матрицей смежности ребер графа называется такая матрица
В = || b
ij
|| (i = 1, …, m; j = 1, …, m, где m – число ребер графа),
что
1,
если ребра g
i
и g
j
имеют общий конец,
b
ij
=
0
в противном случае.
Пусть g
1
,…, g
m
– дуги, а x
1
,…, x
n
– вершины ориентированного
графа G(X). Матрица S = || s
ij
|| (i = 1, …, n – номер вершины графа,
j = 1, …, m – номер дуги графа), такая что
1,
если g
j
исходит из x
i,
s
ij
=
-1, если g
j
заходит в x
i,
0,
если g
j
не инцидентна x
i
называется матрицей инциденций для дуг графа.
Матрица R = || r
ij
|| размером n
× m, где
1,
если x
i
(i = 1, …, n) инцидентна g
j
(j = 1, …, m),
r
ij
=
0
в противном случае
x
1
x
3
x
2
x
4
x
5
Рис. 2.22 – Пример графа для определения матрицы смежности A
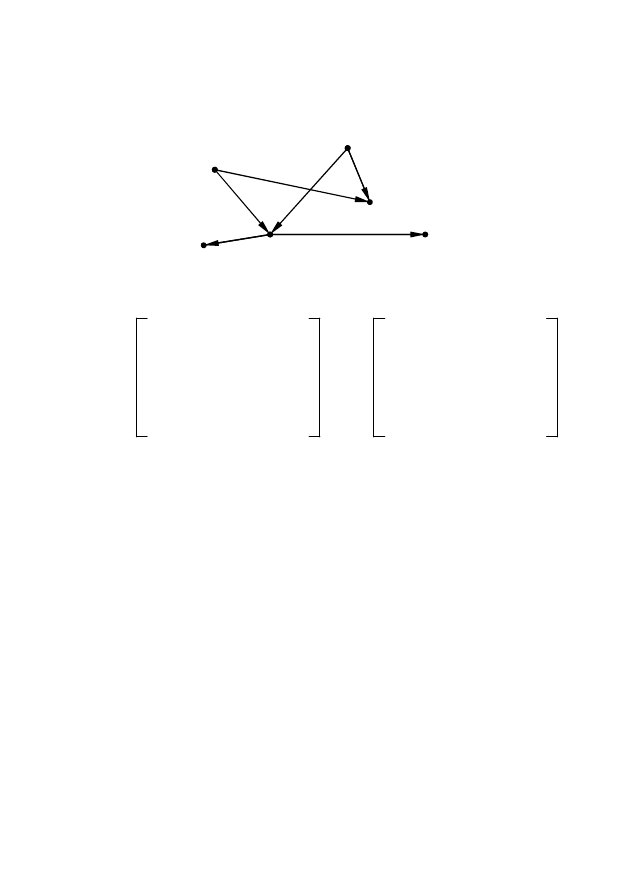
35
называется матрицей инциденций для ребер графа (рис. 2.23).
0 1 0 1 0 0
0 1 0 1 0 0
1 0 1 0 0 0
1 0 1 0 0 0
S =
-1 -1 0 0 0 0
, R =
1 1 0 0 0 0
.
0 0 -1 -1 1 1
0 0 1 1 1 1
0 0 0 0 -1 0
0 0 0 0 1 0
0 0 0 0 0 -1
0 0 0 0 0 1
2.4
Операции
над
графами
Сумма графов
Пусть даны два графа G
1
(X) и G
2
(X) на одном и том же множе-
стве вершин. Тогда суммой G(X), графовG
1
(X) и G
2
(X) является
граф, состоящий из ребер, принадлежащих G
1
(X), либо G
2
(X). Таким
образом, если (x
i
', x
j
')
∈ G
1
(X)и (x
i
'', x
j
'')
∈ G
2
(X), то (x
i
', x
j
')
∈ G(X) и
(x
i
'', x
j
'')
∈ G(X) ∀ (x
i
', x
j
', x
i
'', x
j
'')
∈ X.
Символически сумму двух графов обозначают следующим об-
разом: G(X) = G
1
(X)
∪ G
2
(X). Аналогично определяется сумма n
графов G
i
(X) (i =1, …, n):
n
G(X)
=
∪ G
i
(X)
i =1
как граф, состоящий из ребер, принадлежащих хотя бы одному из
графов G
i
(X) (рис. 2.24, а, б).
Операция суммирования графов обладает переместительным
свойством, то есть G
1
(X)
∪ G
2
(X) = G
2
(X)
∪ G
1
(X).
g
2
g
3
g
1
g
4
g
5
g
6
x
1
x
5
x
4
x
2
x
3
x
6
Рис. 2.23 – Пример графа для определения матриц
инциденций S и R