ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16658
Скачиваний: 202

51
2.10 Сочетания с повторениями
Постановка задачи. Сколько существует выборок, содержащих по m эле-
ментов из множества А = {а
1
, а
2
, …, а
n
}, если в выборки могут входить повто-
ряющиеся элементы и если порядок элементов в выборках безразличен?
Такие выборки называют сочетаниями с повторениями.
Например, если
А = {а, b, c, d},
то выборки длины m = 2 имеют вид:
aа, bb, cc, dd, ab, bc, cd, ac, bd, ad.
Сочетания с повторениями рассмотрим на примерах.
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 2.28
· · · · · · · · · · · · · · · · · · · · · ·
Имеются репродукции с картин Шишкина, Левитана, Поленова и Василь-
ева не менее чем по 10 экземпляров каждой. Требуется выбрать 10 репродукций
в любом сочетании из перечисленных. Сколькими способами это можно сде-
лать?
Закодируем выборку следующим образом. Пусть решено взять три ре-
продукции Шишкина, две – Левитана, одну – Поленова и четыре – Васильева.
Запишем три единицы (это репродукции Шишкина). После них поставим нуль.
Затем запишем две единицы (это репродукции Левитана) и нуль. Затем поста-
вим одну единицу (репродукция Поленова) и нуль. В конце запишем четыре
единицы (репродукции Васильева), но нуль после них не ставим. Получилось
13-значное двоичное число:
1 1 1 0 1 1 0 1 0 1 1 1 1,
где нули отделяют одни репродукции от других.
Очевидно, что всякое распределение трех нулей в этом коде дает некото-
рый вариант выбора репродукций. Например:
1111001011111 – взято четыре репродукции Шишкина (об этом говорят
первые четыре единицы в коде), ни одной репродукции Левитана (так как меж-
ду двумя нулями нет единиц), одна репродукция Поленова (одна единица после
второго нуля) и пять репродукций Васильева (последние пять единиц).
0001111111111 – взято 10 репродукций Васильева. Все другие репродук-
ции в выборку не вошли. И так далее.
52
Таким образом, число вариантов выбора репродукций равно числу всех
возможных 13-значных двоичных кодов, в каждом из которых содержится точ-
но десять единиц:
10
10
4
13
13!
286,
10! 3!
С
С
=
=
=
⋅
ɺ
где символом
10
4
Сɺ
обозначено число сочетаний с повторениями из четырех эле-
ментов по 10.
В общем случае если из n элементов множества А составляют выборки,
каждая из которых содержит m элементов, причём повторения возможны, то
число всех таких выборок равно:
1
1
1
.
−
+ −
+ −
=
=
ɺ
m
m
n
n
n m
n m
С
C
C
(2.17)
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 2.29
· · · · · · · · · · · · · · · · · · · · · ·
По трём ящикам требуется разложить 45 гаек таким образом, чтобы в
каждом ящике оказалось хотя бы по десять гаек. Сколькими способами это
можно сделать?
По 10 гаек в каждый из ящиков можно положить заранее. Тогда для про-
извольной раскладки останется 15 гаек. Следовательно т = 15, п = 3. По фор-
муле (2.17) находим:
15
15
3
3 15 1
17!
16 17
136.
15! 2!
1 2
С
C
+ −
⋅
=
=
=
=
⋅
⋅
ɺ
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
В магазине продают четыре вида конфет. Сколькими спо-
собами можно купить 15 конфет в произвольном наборе?
2.
Продаются тетради пяти цветов: с синей, фиолетовой,
красной, зеленой и оранжевой обложками.
а. Требуется купить 10 тетрадей любого цвета. Скольким спо-
собами это можно сделать?
б. Требуется купить 15 тетрадей. Пять из них должны быть с
фиолетовой обложкой, а обложки всех остальных тетрадей могут
быть любого цвета, кроме фиолетового. Сколькими способами воз-
можна такая покупка?

53
в. Требуется купить 16 тетрадей, среди которых точно 4 тет-
ради должны быть с зеленой обложкой и точно 5 тетрадей – с оран-
жевой. Цвет обложки остальных тетрадей значения не имеет.
Сколькими способами возможна такая покупка?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
54
3 Теория графов
3.1 Понятие графа
Теория графов как один из разделов дискретной математики в настоящее
время успешно применяется в социологии, экономике, биологии, медицине,
химии, психологии и других науках. Но особенно велико её значение в самой
дискретной математике, в таких её разделах, как программирование, теория ло-
гических схем, контактных структур, многотактных дискретных автоматов,
теория бинарных отношений и др.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Граф – это множество V точек, определенным образом соеди-
ненных между собой линиями, необязательно прямыми. Точки
множества V называются вершинами графа, а соединяющие их ли-
нии – ребрами. Вершины можно обозначать не только точками, но и
кружкáми. Вершины графа обычно нумеруют десятичными числа-
ми, но могут использоваться и любые другие знаки. Граф, вершины
которого каким-либо образом пронумерованы, называется помечен-
ным графом.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
В общем случае те или иные пары вершин графа могут соединяться не-
сколькими рёбрами. Такие ребра называют кратными (параллельными). Кроме
того, граф может содержать ребра, соединяющие какую-либо вершину саму с
собой. Такие ребра называются пéтлями. Вершина называется изолированной,
если у нее нет петель, и из нее не выходит ни одного ребра.
Обычно различают три типа графов: простые (или линейные по термино-
логии [51]), псевдографы и мультиграфы. Граф, согласно [51, с. 56], называется
линейным, если любые две его вершины соединены не более чем одним ребром
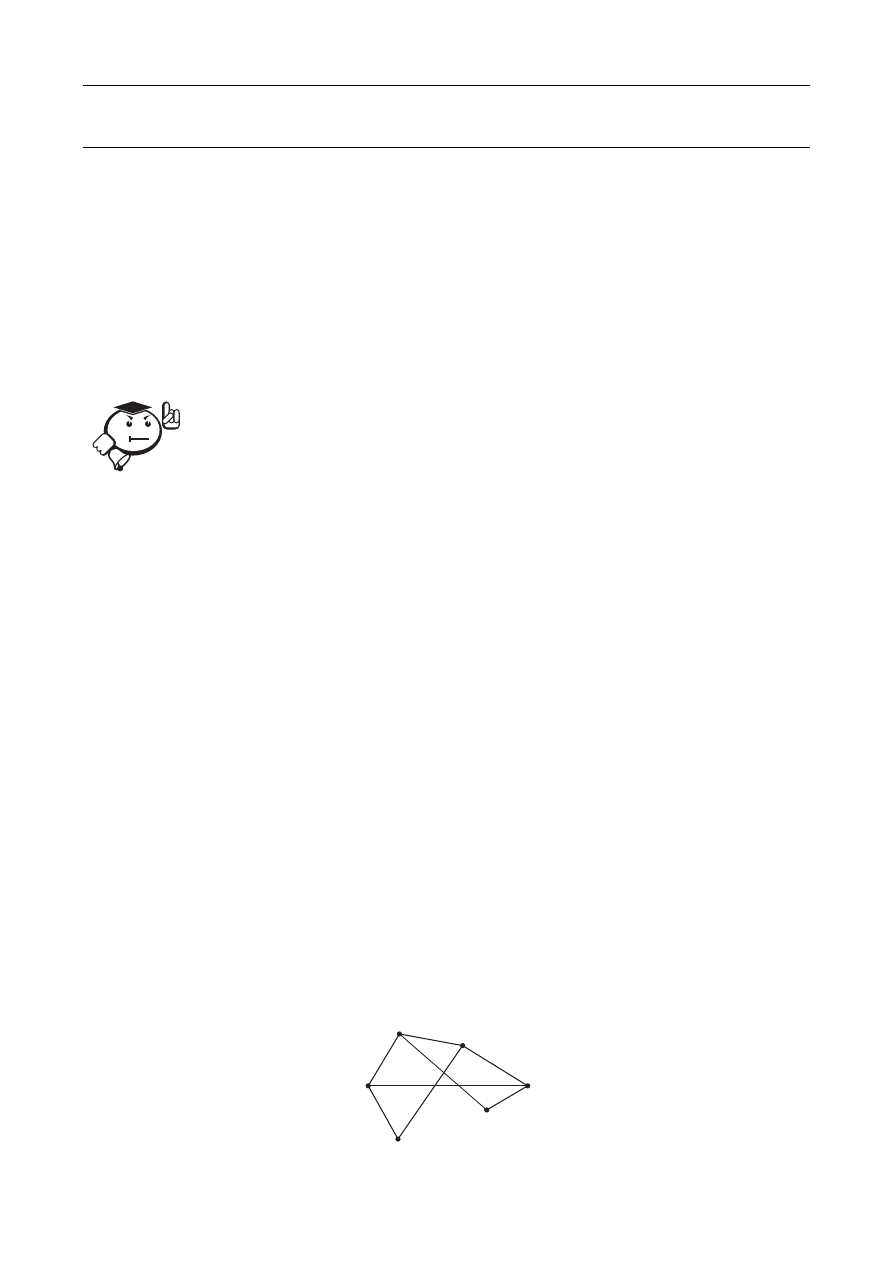
и каждое ребро соединяет различные вершины. Пример линейного (простого)
графа приведен на рисунке 3.1.
Рис. 3.1
1
2
3
4
5
6
55
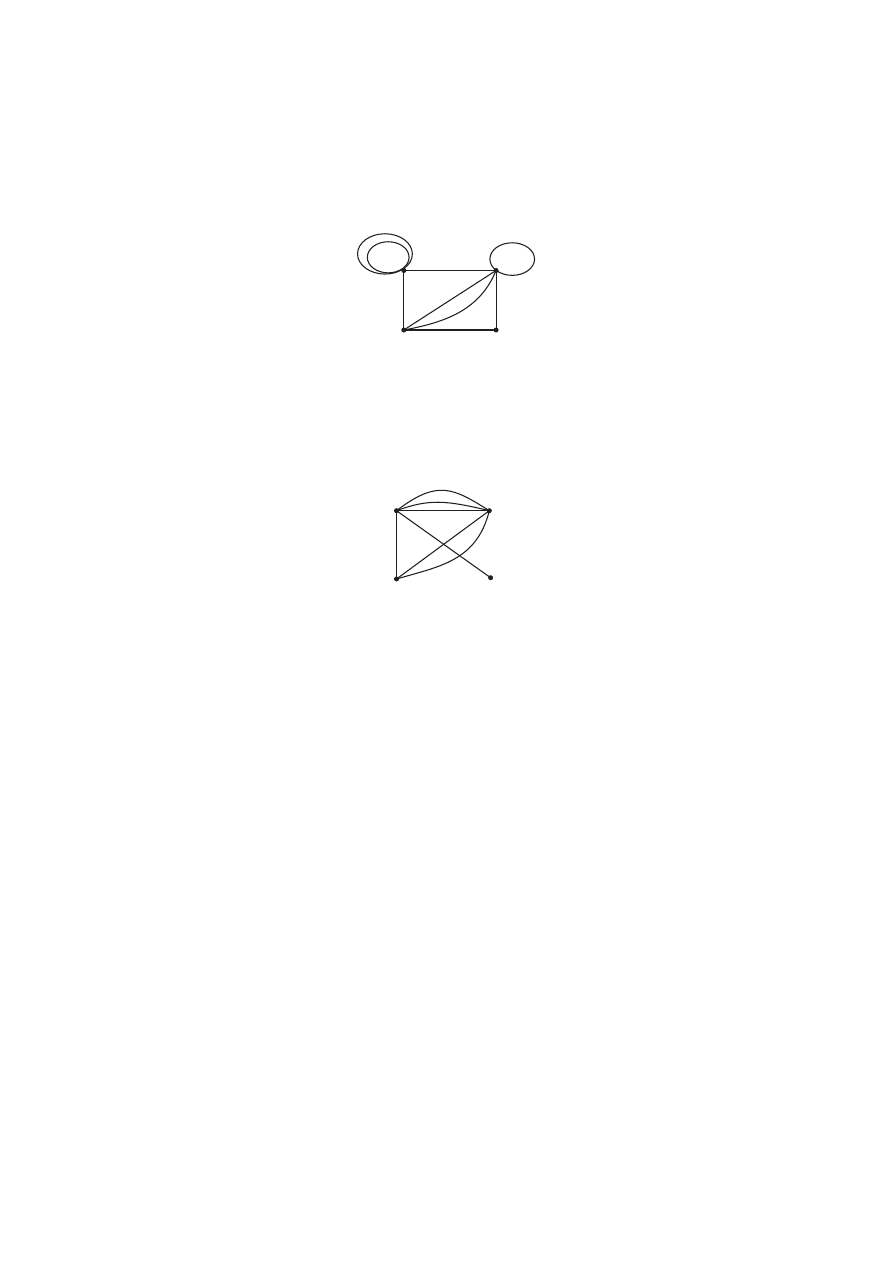
Граф, содержащий петли или кратные ребра (или то и другое), называется
псевдографом [8, с. 101; 33, с. 161]. Пример псевдографа приведен на рисун-
ке 3.2, где вершина 1 имеет две кратные петли, вершина 2 – одиночную петлю,
а вершины 2 и 3 соединены кратными ребрами.
Рис. 3.2
Псевдограф без петель называется мультиграфом [8, с. 101; 33, с. 161].
Пример мультиграфа приведен на рисунке 3.3.
Рис. 3.3
Однако в данном пособии использование этой терминологии большей ча-
стью не является необходимостью, поэтому все графы в дальнейшем будем
называть просто графами, за исключением тех случаев, когда потребуется
уточнить, может ли граф содержать петли и кратные рёбра. Обозначать поме-
ченные графы будем буквой G.
Помеченный граф может быть задан не только рисунком, но и аналитиче-
ски, множеством неупорядоченных пар номеров вершин, где каждая пара но-
меров обозначает соответствующее ребро. Например, аналитическое представ-
ление графа, изображённого на рисунке 3.1, имеет вид:
G = {{1,2}, {1,3}, {1,6}, {2,4}, {2,5}, {3,4}, {3,5}, {4,6}}.
При удалении из графа G некоторых вершин будут удалены и выходящие
из них ребра. Оставшиеся вершины и ребра образуют подграф G
′ графа G [14].
Для всякого подграфа справедливы утверждения:
V
′ ⊆ V и E′ ⊆ E,
где V и E – множества вершин и ребер графа G соответственно; V
′ и E′ – мно-
жества вершин и ребер подграфа G
′. Отсюда следует, что всякий граф является
подграфом самого себя.
1
2
3
4
1
2
3
4