ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16653
Скачиваний: 202

41
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Сколько существует трёхразрядных восьмеричных чисел, в
которых нет цифр 0,1,2 и нет повторяющихся цифр?
2.
В тире 10 мишеней. Перед ними три стрелка. Каждый стре-
лок произвольно выбирает себе мишень, но так, что каждую ми-
шень выбирает не более чем один стрелок. Сколькими способами
возможен выбор?
3.
Из восьмеричных цифр образуют пятизначные числа, в ко-
торых нет повторов цифр. Сколько существует таких чисел при
условии, что каждое число начинается с единицы и оканчивается
тройкой?
4.
Четыре школьника выбирают по одной книге из 9 предло-
женных. Все книги разные. Сколькими способами возможен выбор?
5.
Сколько существует пятизначных восьмеричных чисел, в
каждом из которых нет повторов цифр, и в каждом числе последняя
цифра на единицу больше первой? С нуля числа не начинаются.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
2.8 Размещения с повторениями
Постановка задачи. Из множества, содержащего n элементов, образуют
размещения с повторениями, т. е. упорядоченные последовательности длины m,
в которых одни и те же элементы могут повторяться. Сколько существует таких
последовательностей?
Воспользуемся правилом произведения. Так как в заданном множестве n
элементов, то первый элемент может быть выбран n способами, второй – n спо-
собами и т. д. до элемента с номером m. В результате получаем
,
=
ɺ
m
m
n
А
n
(2.10)
где точка над буквой A обозначает: размещения могут быть с повторениями.
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 2.20
· · · · · · · · · · · · · · · · · · · · · ·
Сколько существует трёхразрядных чисел, которые могут быть образова-
ны из цифр 1, 2, 3, 4, 5, если повторы разрешены?

42
Согласно условию данного примера n = 5, m = 3, т. е. каждое число из ис-
комых – это трёхэлементная упорядоченная последовательность цифр, где
цифры могут повторяться. По формуле (2.10) получаем:
3
5
3
5
125.
=
=
ɺ
А
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 2.21
· · · · · · · · · · · · · · · · · · · · · ·
Сколько существует пятиразрядных десятичных чисел, в которых воз-
можны любые повторы цифр?
В условии нет оговорки, что числа могут начинаться с нуля. Это значит,
что на месте старшего разряда можно поставить любую цифру, кроме нуля. На
месте остальных разрядов могут стоять и нули.
Сначала задачу решим в общем виде. Пусть n – основание системы счис-
ления, m – длина выборки. Первую цифру из n можно выбрать n – 1 способами
(с нуля числа не начинаются). Во всех остальных разрядах цифры выбираются
n способами каждая. Таким образом, число N m-разрядных чисел равно:
N = (n – 1)
1
−
m
n
Аɺ
= (n – 1) n
m
– 1
.
(2.11)
Согласно условию данного примера, n = 10, m = 5. Следовательно, по
формуле (2.11) получаем:
N = 9⋅10
4
= 90 000.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Сколько существует двузначных десятичных чисел? Числа
могут начинаться с нуля.
2.
Сколько существует пятизначных чисел троичной системы
счисления? Числа с нуля не начинаются.
3.
Сколько слов длины 12 можно составить из букв а и b?
4.
Из элементов множества А = {а, б, в, г, д, е} образуют по-
следовательности длины 3, каждая из которых начинается с бук-
вы б. Сколько всего существует таких последовательностей, если
повторы букв возможны?
5.
Из элементов множества А = {а, б, в, г, д, е} образуют по-
следовательности длины 3, каждая из которых не начинается с бук-

43
вы д. Сколько всего существует таких последовательностей, если
повторы букв возможны?
6.
Сколько существует 12-значных двоичных чисел, если все
они начинаются с единицы и все оканчиваются единицей?
7.
Сколько существует 7-значных троичных чисел, не содер-
жащих нулей?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
2.9 Сочетания без повторений
Постановка задачи. Из множества А, содержащего n элементов, выделили
некоторое подмножество, состоящее из m элементов (m ≤ n). Сколько суще-
ствует таких подмножеств?
Подмножества множества А, содержащие m элементов, получили назва-
ние сочетаний из n элементов по m, где n = |A|. Число всех сочетаний из n эле-
ментов по m во многих литературных источниках принято обозначать знаком
m
n
С
[7; 16; 17; 20; 23; 33; 38; 40; 46], где нижний индекс n – это число всех тех
элементов, из которых осуществляются выборки. Верхний индекс m показыва-
ет, сколько элементов входит в выборку. Существуют и другие обозначения
числа сочетаний, например C(n, k) [14; 35], а также
n
C
m
[51] и
n
m
[46; 52; 57].
Размещения, описываемые формулой (2.7), это m-элементные последова-
тельности, отличающиеся одна от другой как элементами, так и порядком запи-
си элементов. В отличие от размещений сочетания – это неупорядоченные по-
следовательности m элементов. Сочетания отличаются одно от другого только
элементами, а порядок расположения их в последовательности не имеет значе-
ния. Следовательно, если число
m
n
А
разделить на m!, то получим формулу для
числа сочетаний из n элементов по m:
!
.
!
!(
)!
=
=
−
m
m
n
n
A
n
С
m
m n
m
(2.12)
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 2.22
· · · · · · · · · · · · · · · · · · · · · ·
Сколько существует семизначных двоичных чисел, содержащих точно
три единицы? Числа могут начинаться с нуля.
44
Переформулируем задачу: сколькими способами можно выбрать три ме-
ста из семи, чтобы поставить на них по единице, а остальные заполнить нуля-
ми? Очевидно, что все такие выборки являются сочетаниями, поскольку поря-
док выбора мест значения не имеет. В данном случае n = 7, m = 3,
следовательно, согласно формуле (2.12), искомое число сочетаний равно:
3
7
7!
7!
5 6 7
35.
3!(7 3)! 3! 4! 1 2 3
С
⋅ ⋅
=
=
=
=
−
⋅
⋅ ⋅
Эту задачу можно сформулировать иначе: сколько существует семизнач-
ных чисел двоичной системы счисления, содержащих точно четыре нуля?
В этом случае n = 7, m = 4. По формуле (2.12) находим:
4
7
7!
7!
5 6 7
35.
4!(7 4)! 4! 3! 1 2 3
С
⋅ ⋅
=
=
=
=
−
⋅
⋅ ⋅
Ответ получился такой же, как и при первой формулировке. В общем
случае справедливым является равенство:
.
m
n
n
m
n
C
С
−
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 2.23
· · · · · · · · · · · · · · · · · · · · · ·
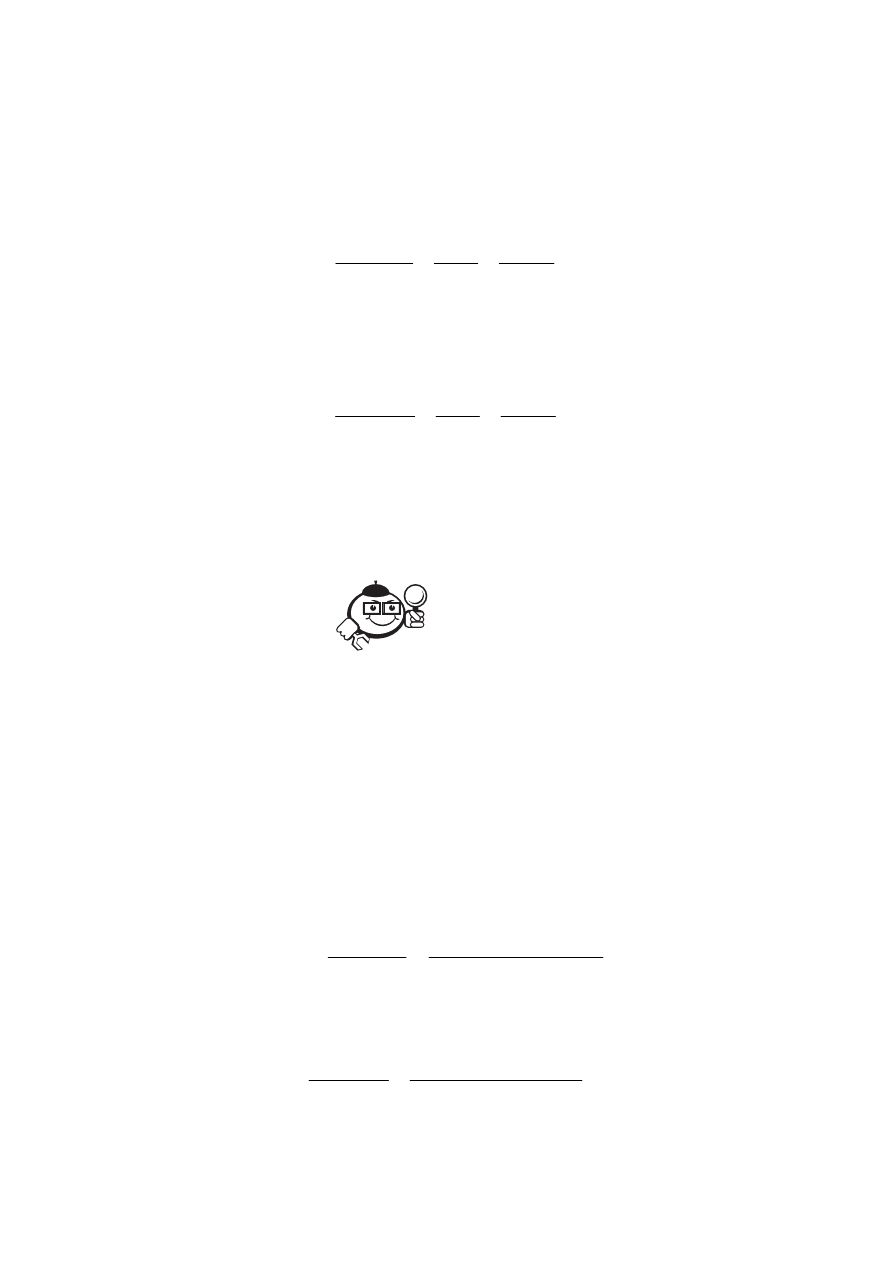
На плоскости проведена окружность. На ней поставлено n точек. Каждые
две из этих точек соединены отрезком. Отрезки внутри круга образуют внут-
ренние точки пересечения. При этом в каждой из них пересекаются точно два
отрезка. Сколько точек пересечения имеется внутри круга? Точки пересечения
линий с окружностью не учитывать.
Чтобы получить одну точку пересечения, необходимо взять четыре точки
на окружности. Следовательно, точек пересечения внутри круга столько же,
сколько существует четвёрок точек, расположенных на окружности. Количе-
ство таких четвёрок, согласно формуле (2.12), равно:
.
24
)
3
)(
2
)(
1
(
)!
4
(
!
4
!
4
−
−
−
=
−
=
n
n
n
n
n
n
С
n
(2.13)
На рисунке 2.1 изображена окружность, на которой поставлено 7 точек,
то есть n = 7. Подставим в формулу (2.13) значение n = 7:
4
7
7!
7(7 1)(7 2)(7 3)
35.
4!(7 4)!
24
С
−
−
−
=
=
=
−
45
Рис. 2.1
Таким образом, внутри круга имеется 35 точек пересечения отрезков.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 2.24
· · · · · · · · · · · · · · · · · · · · · ·
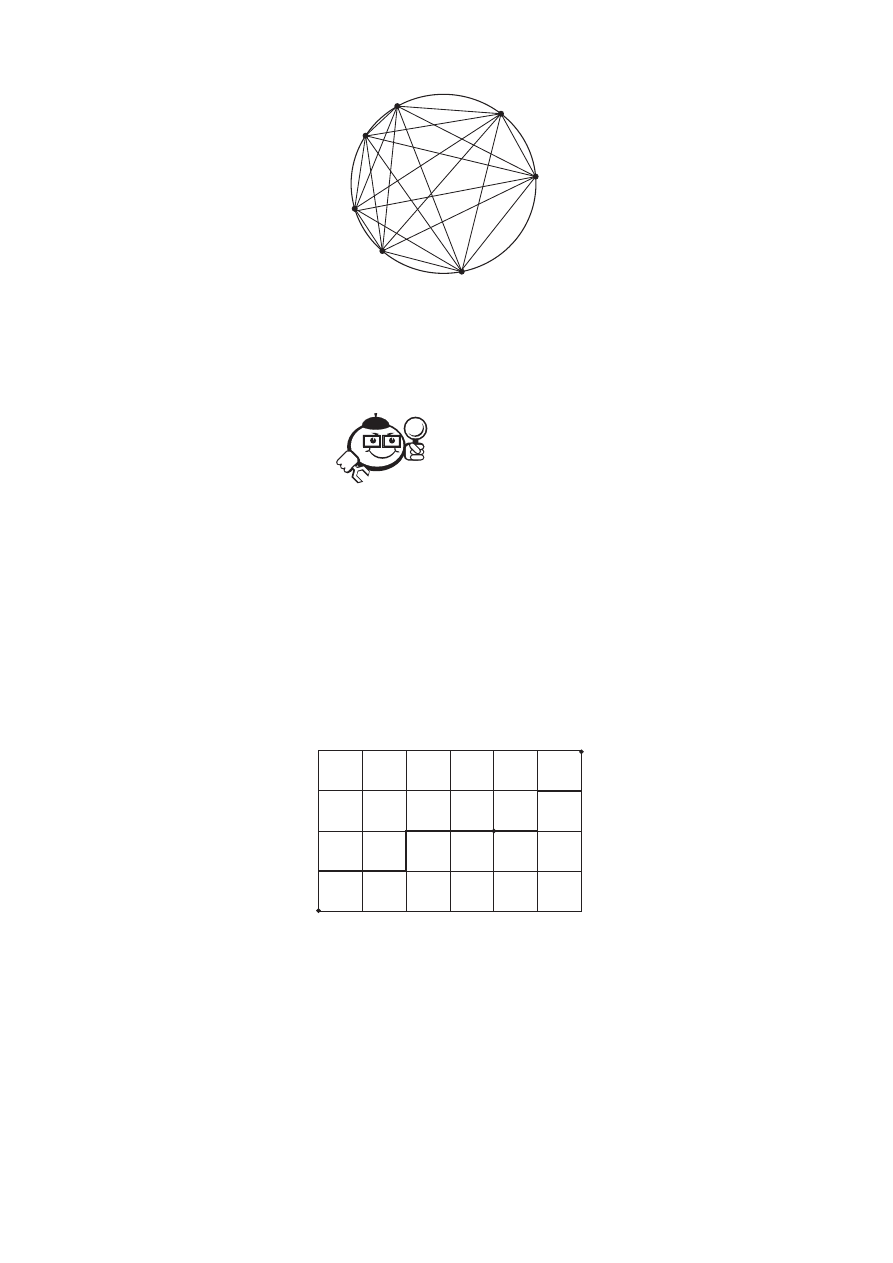
На рисунке 2.2 изображён шахматный город размером m × n квадратов,
где n = 4 – число квадратов (клеток) по вертикали, m = 6 – число квадратов по
горизонтали. Движение в шахматном городе возможно лишь по вертикальным
и горизонтальным отрезкам. Определить число кратчайших путей:
1)
от точки А до точки В;
2)
от точки А до точки В с обязательным заходом в точку С;
3)
от точки А до точки В, без захода в точку С.
Рис. 2.2
Решим задачу, рассуждая следующим образом:
1) кратчайший путь от точки А до точки В состоит из n + m отрезков, при-
чем в нём содержится точно n вертикальных отрезков и точно m – горизонталь-
ных. Закодируем пути. Нулём обозначим движение вверх, единицей – движение
вправо. Тогда каждому пути будет соответствовать (m + n)-разрядный двоич-
ный код, содержащий точно m единиц. И наоборот, каждому (m + n)-
1
2
3
4
5
6
7
A
B
C
n
m