ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16678
Скачиваний: 202
121
1
1 1
1 1 1
1 1
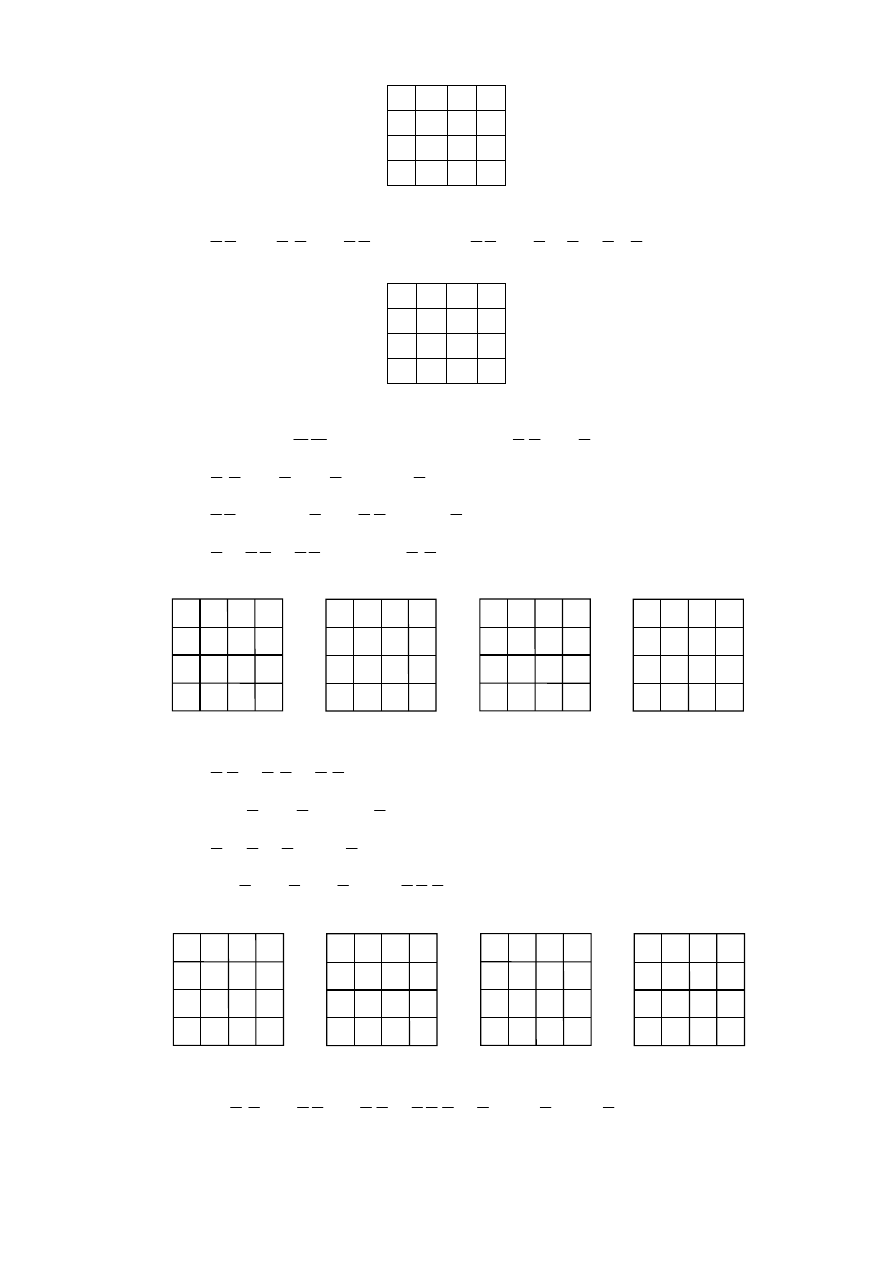
Рис. 5.39
20.
f
BD
AC D
ABC
ABCD
ABC
AC D
ABCD
=
+
+
+
+
+
+
(рис. 5.40).
1 1
1 1
1 1
1 1 1 1
Рис. 5.40
21.
;
AC
D
C
CD
B
f
+
+
+
=
f
B CD
C D
AD
= +
+
+
(рис. 5.41).
22.
f
C D
AD
AC
BC
AC D
=
+
+
+
+
(рис. 5.42).
23.
f
AB
AC
BD
ACD
ABD
=
+
+
+
+
(рис. 5.43).
24.
f
C
BD
AB
ABD
A D
= +
+
+
+
(рис. 5.44).
25.
f
C D
A D
AC
BC
ACD
=
+
+
+
+
(рис. 5.45).
26.
f
D
AC
BC
ABC
=
+
+
+
(рис. 5.46).
27.
f
C
D
AB
A B
= +
+
+
(рис. 5.47).
28.
f
ACD
BCD
ACD
BC D
=
+
+
+
(рис. 5.48).
29.
f
A C D
ABC
AB D
BC D
ABC
ABD
ACD
BCD
=
+
+
+
+
+
+
+
(рис. 5.49).
Рис. 5.41
1
1 1
1
1 1 1 1
1 1
1 1
1
Рис. 5.42
1
1 1
1
1 1 1
1
1
1 1
1
Рис. 5.43
1 1
1
1
1 1 1 1
1 1 1
Рис. 5.44
1
1
1
1 1
1
1
1 1
1 1 1 1
Рис. 5.45
1
1 1
1
1 1 1
1
1
1
1 1
Рис. 5.46
1
1
1 1 1 1
1 1 1 1
1 1
Рис. 5.47
1
1 1
1
1
1 1
1 1
1
1 1 1 1
Рис. 5.48
1
1
1 1
1
1 1
1

122
30.
f
BCD
ABD
BCD
A B D
=
+
+
+
(рис. 5.50).
31.
;
f
ACD
ACD
ACD
BC
BD
=
+
+
+
+
f
ACD
ACD
ACD
BC
A B
=
+
+
+
+
(рис. 5.51).
32.
;
D
C
B
D
B
A
BCD
D
A
f
+
+
+
=
;
C
B
A
D
B
A
BCD
D
A
f
+
+
+
=
;
C
B
A
CD
A
BCD
D
A
f
+
+
+
=
f
AD
ABC
ACD
ABC
=
+
+
+
(рис. 5.52).
33.
f
A B
AC
ABD
AC D
=
+
+
+
(рис. 5.53).
34.
f
A D
BD
ACD
=
+
+
(рис. 5.54).
35.
f
C
D
AB
= +
+
(рис. 5.55).
36.
f
AD
CD
ACD
BD
=
+
+
+
(рис. 5.56).
37.
f
A B
ACD
BCD
ABC D
ABCD
=
+
+
+
+
(рис. 5.57).
38.
f
ABC
ABD
ACD
BCD
ACD
ABC
BCD
=
+
+
+
+
+
+
(рис. 5.58).
39.
f
AD
ABC
AB C
ABD
=
+
+
+
(рис. 5.59).
40.
f
AC D
ABD
BCD
ABCD
A BCD
ABCD
=
+
+
+
+
+
(рис. 5.60).
Рис. 5.53
1
1
1 1 1
1 1
1
1 1
Рис. 5.54
1 1
1
1 1 1 1
1 1
Рис. 5.55
1
1
1 1 1 1
1 1 1 1
1 1
1
Рис. 5.56
1
1 1
1
1 1 1 1
1
Рис. 5.49
1
1
1 1 1
1
1
1 1
1
Рис. 5.50
1
1
1 1
1 1
1 1
Рис. 5.51
1
1
1
1 1 1 1
1
1 1
Рис. 5.52
1 1
1 1
1 1
1 1
1
Рис. 5.57
1
1
1
1
1 1
1 1
Рис. 5.58
1
1
1 1 1
1
1
1
1
Рис. 5.59
1
1 1
1 1 1
1
1 1
Рис. 5.60
1
1
1
1
1 1
1

123
41.
f
AB
BD
AC
ACE
=
+
+
+
(рис. 5.61).
42.
f
AC
CD
ABE
ABDE
ABC DE
ABC DE
=
+
+
+
+
+
(рис. 5.62).
43.
f
BE
AC
BCD
ABC DE
=
+
+
+
(рис. 5.63).
44.
;
E
C
B
E
C
A
ACE
ABE
D
f
+
+
+
+
=
f
D
ABE
ACE
ABC
=
+
+
+
(рис. 5.64).
45.
f
C
BE
ABE
= +
+
(рис. 5.65).
46.
f
СD
AB
BCE
ABCE
ABCDE
=
+
+
+
+
(рис. 5.66).
5.9 Примеры минимизации ДНФ с учётом
неопределённых состояний
Булева функция называется полностью (всюду) определённой, если для
каждого набора значений аргументов известно, чему она равна – нулю или еди-
нице. Если же существует хотя бы один набор, на котором значение функции
не указано, то такая функция называется неполностью определённой (в [51] их
называют частичными функциями).
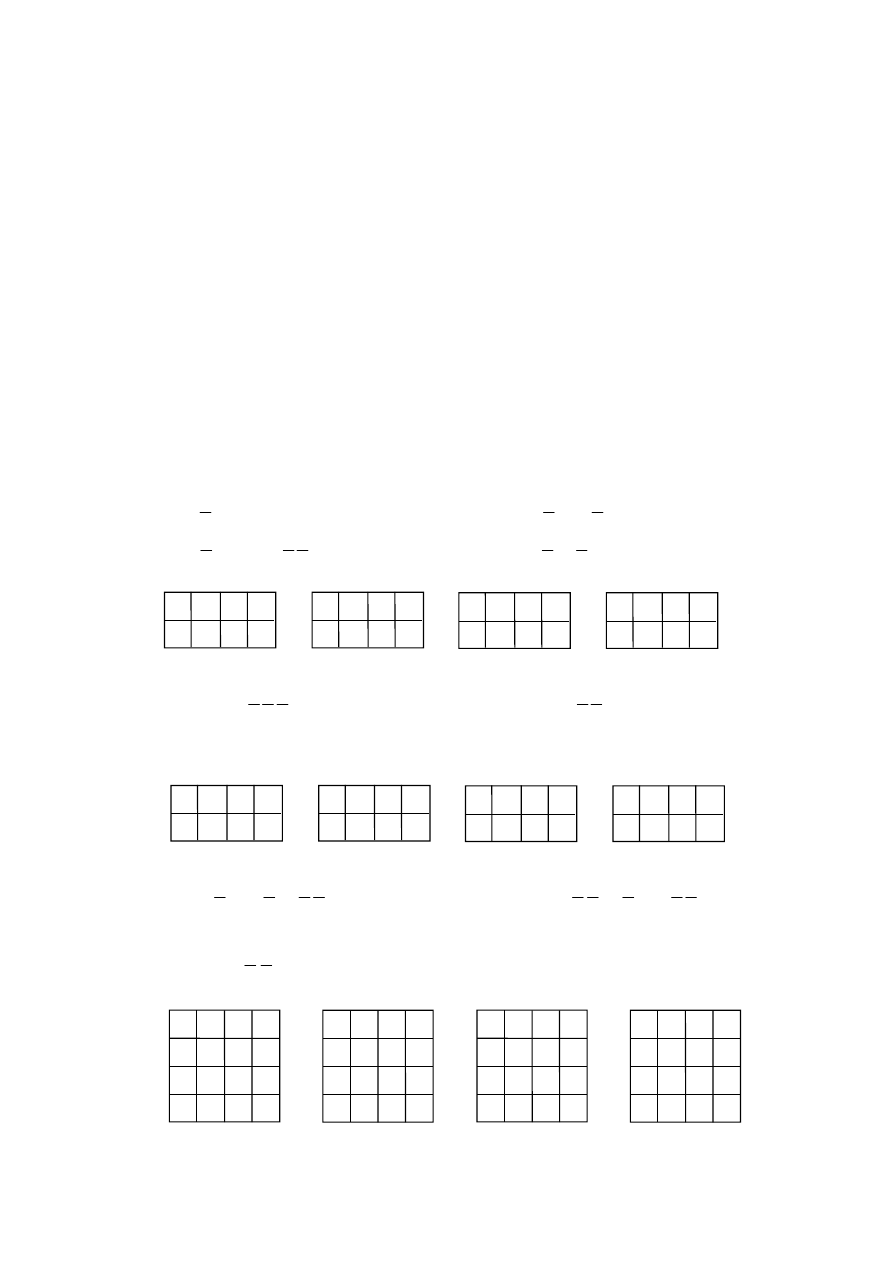
Рис. 5.61
1 1
1
1 1
1
1 1 1 1
1
1
1 1
1
1 1
1
1 1 1 1
1
Рис. 5.62
1
1 1 1
1 1
1
1
1
1
1 1
1 1 1
1 1
Рис. 5.63
1
1 1
1
1 1 1 1
1 1
1
1
1
1 1
1
1
Рис. 5.64
1 1
1 1 1 1
1 1 1 1
1
1
1 1 1 1
1 1 1 1
1 1
Рис. 5.65
1 1
1
1 1
1
1
1
1
1
1
1
1
1
1 1 1 1
1 1 1 1
Рис. 5.66
1 1
1 1 1
1 1
1
1
1 1
1 1 1
1 1
1
124
Для обозначения неопределённых состояний на картах Вейча и в табли-
цах соответствия будем применять крестик в виде знака арифметического
умножения «×».
Наборы, на которых функция не определена, иногда называют запрещён-
ными состояниями, а в [48] им дано название избыточные комбинации.
Чтобы минимизировать неполностью определённую функцию, её сначала
необходимо доопределить, то есть крестики заменить единицами или нулями,
так как в аналитическом представлении неполностью определённой функции
крестик поставить некуда. При этом заменять крестики единицами необходимо
только в том случае, если с их участием число букв простой импликанты
уменьшается. Для иллюстрации этого ниже приведено 28 примеров.
Минимизация с учётом неопределённых состояний очень часто осу-
ществляется неоднозначно. Но в данном параграфе из всех возможных мини-
мальных форм приводится только по одному варианту.
1.
f
B
=
(рис. 5.67).
3.
f
BC
ABC
=
+
(рис. 5.69).
2.
f
C
AB
AB
= +
+
(рис. 5.68).
4.
f
AB
AB
=
+
(рис. 5.70).
5.
f
AB
ABC
=
+
(рис. 5.71).
7.
f
AB
AB
=
+
(рис. 5.73).
6.
f
AB
BC
AC
=
+
+
(рис. 5.72).
8.
1
f =
(рис. 5.74).
9.
f
BD
CD
BCD
=
+
+
(рис. 5.75).
11.
f
AD
CD
BD
ABD
=
+
+
+
(рис. 5.77).
10.
f
A C D
BCD
= +
+
(рис. 5.76).
12.
f
C
AB
= +
(рис. 5.78).
Рис. 5.67
1
×
1
×
1
×
×
1
1
×
1
× 1
×
1
1
1
× ×
1
1
1
×
Рис. 5.68
Рис. 5.69
Рис. 5.70
Рис. 5.71
×
× 1
1
1
×
×
1
×
1 1
1
1
×
1
1 ×
1
×
× 1
1
×
Рис. 5.72
Рис. 5.73
Рис. 5.74
Рис. 5.75
1
1 1
×
× ×
1
×
× 1
Рис. 5.76
× 1
1
1 × 1
1 ×
×
1 ×
1
Рис. 5.77
1 ×
× 1
1
1
× 1
1 1 × 1
Рис. 5.78
1
× 1
×
1 × 1
× × × ×
× 1

125
13.
f
BD
C D
AB
BCD
=
+
+
+
(рис. 5.79).
14.
f
D
BC
ABC
=
+
+
(рис. 5.80).
15.
f
D
ABC
ABC
ABC
=
+
+
+
(рис. 5.81).
16.
f
AD
BD C
=
+
+
(рис. 5.82).
17.
f
BD
BC
BCD
=
+
+
(рис. 5.83). 19.
f
BD
AB
BCD
=
+
+
(рис. 5.85).
18.
f
D
BC
= +
(рис. 5.84).
20.
f
D
AC
=
+
(рис. 5.86).
21.
f
C D
BC
AD
=
+
+
(рис. 5.87). 23.
f
ABD
AC
A B D
=
+
+
(рис. 5.89).
22.
f
A
B D
BD
= +
+
(рис. 5.88).
24.
f
D
AB
= +
(рис. 5.90).
25.
f
C D
AC
CD
=
+
+
(рис. 5.91).
26.
f
AC
AC
ABE
=
+
+
(рис. 5.92).
27.
f
CD
ABDE
C DE
ABDE
=
+
+
+
(рис. 5.93).
Рис. 5.87
×
1 ×
1
1 ×
×
×
1 ×
Рис. 5.88
× 1
× 1 1 ×
1 1
1 × × ×
Рис. 5.89
×
×
1 1 1
× ×
×
1 1
Рис. 5.90
×
×
×
1 × × 1
1 × × 1
× 1 ×
Рис. 5.79
1
×
× 1
1 ×
×
× × 1 ×
Рис. 5.80
1
1 ×
1
1
×
1 1
× × × ×
Рис. 5.81
1
× × 1 1
1 × × ×
1
1
Рис. 5.82
×
1 1
1
× 1 1
× ×
1 × ×
Рис. 5.83
× ×
1 ×
1
× 1 ×
× 1 1 1
Рис. 5.84
1
× ×
1
×
×
× 1 ×
1 1 × ×
Рис. 5.85
×
1
×
×
1 ×
× 1 1 1
× ×
Рис. 5.86
1
×
1 1 × ×
1 × 1 ×
× ×
Рис. 5.91
× 1
×
× ×
× 1
× ×
×
×
× 1
×
× × 1
× 1 1
× 1
1
Рис. 5.92
×
× ×
× 1 × ×
×
× ×
1
1
1
1 ×
×
×
× ×
×
×
× × 1