ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16674
Скачиваний: 202
131
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.4
· · · · · · · · · · · · · · · · · · · · · · ·
( , , ) (3, 5);
f A B C =
[2, 6].
На рисунке 6.11 – СДНФ; на рисунке 6.12 – СДНФ инверсии. Минималь-
ная ДНФ инверсии:
;
f
AB
AB
С
=
+
+
минимальная КНФ:
(
)(
) .
f
A
B A
B С
=
+
+
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.5
· · · · · · · · · · · · · · · · · · · · · · ·
( , , , ) (1, 3, 4, 9,10,11,12);
f A B C D =
[5, 7, 8, 13, 15].
На рисунке 6.13 – СДНФ; на рисунке 6.14 – СДНФ инверсии. Минималь-
ная ДНФ инверсии:
;
f
BC
ABD
=
+
минимальная КНФ:
.
)
)(
(
D
B
A
C
B
f
+
+
+
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.6
· · · · · · · · · · · · · · · · · · · · · · ·
( , , , ) (0, 4, 7, 8,10,11,14);
f A B C D =
[1, 6, 9, 12].
Рисунок 6.15 – СДНФ; рисунок 6.16 – инверсия. Минимальная ДНФ ин-
версии:
.
f
CD
ABD
ABC
=
+
+
Минимальная КНФ:
.
)
)(
)(
(
C
B
A
D
B
A
D
C
f
+
+
+
+
+
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
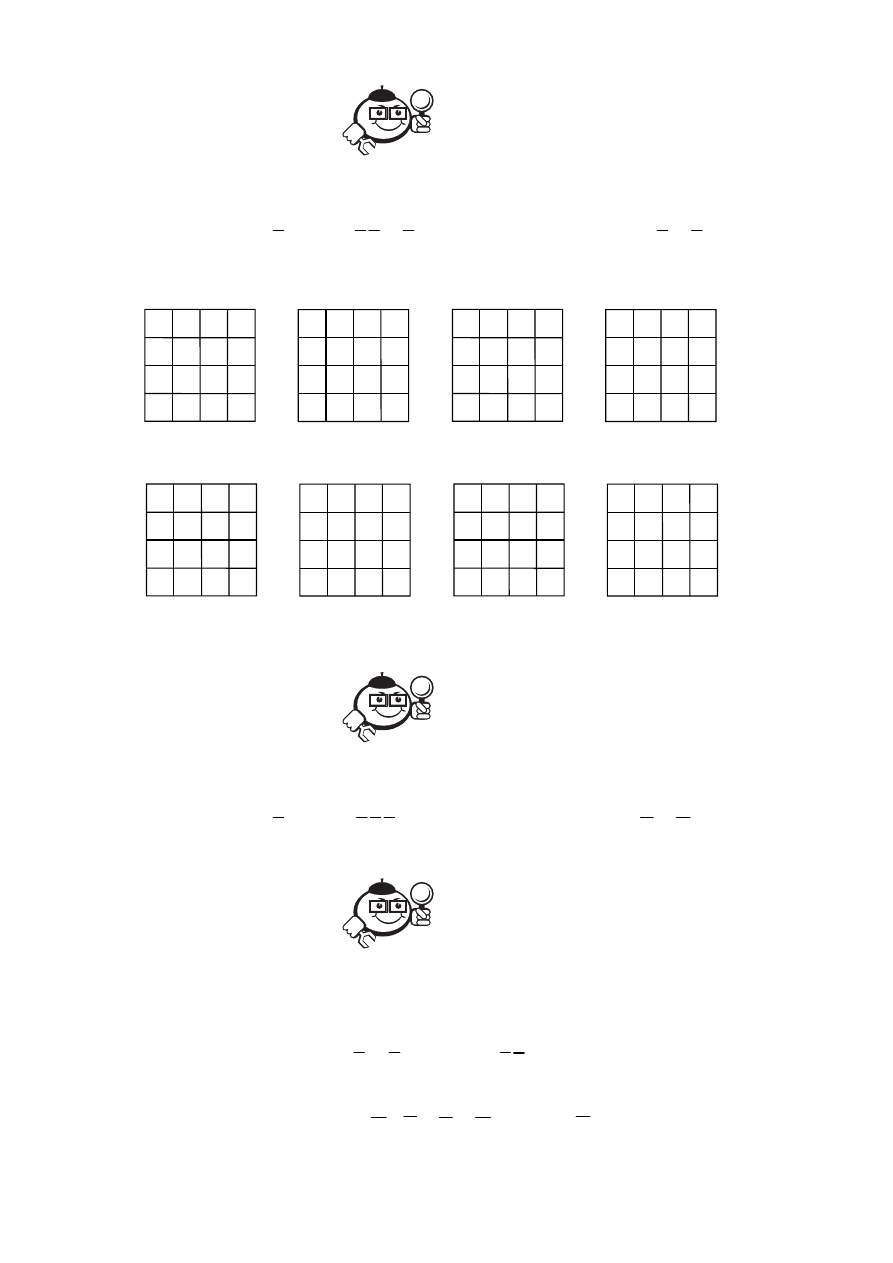
Рис. 6.13
1
1
× × × ×
1 1 1 1
× 1
Рис. 6.14
1
1
× × × ×
×
1 1
Рис. 6.15
1
1
1
1
1
Рис. 6.16
1
1
1
1
Рис. 6.17
1
1
1
× × × ×
1
1 1
× 1 1
Рис. 6.18
1
× × × ×
1
×
1
Рис. 6.19
1
1
× 1 × 1
1
1 ×
1
Рис. 6.20
1
1
×
×
1
1 1
× 1
×
×
×
×
1
1
×
×
×
×
1

132
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.7
· · · · · · · · · · · · · · · · · · · · · · ·
( , , , ) (1, 2, 3, 4, 6, 9,10,12);
f A B C D =
[5, 7, 8, 13, 15].
Рисунок 6.17 – СДНФ; рисунок 6.18 – инверсия. Минимальная ДНФ ин-
версии:
.
f
ABC
ACD
BCD
=
+
+
Минимальная КНФ:
.
)
)(
)(
(
D
C
B
D
C
A
C
B
A
f
+
+
+
+
+
+
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.8
· · · · · · · · · · · · · · · · · · · · · · ·
( , , , ) (0, 4, 5, 8,11,14,15);
f A B C D =
[7, 10, 13].
На рисунке 6.19 – СДНФ; на рисунке 6.20 – СДНФ инверсии. Минималь-
ная ДНФ инверсии:
.
f
AC
BCD
ABC
=
+
+
Минимальная КНФ:
.
)
)(
)(
(
C
B
A
D
C
B
C
A
f
+
+
+
+
+
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
6.4 Алгебра Жегалкина
Иван Иванович Жегалкин – профессор МГУ, специалист по математиче-
ской логике (1869–1947).
В алгебре Жегалкина две операции – конъюнкция и сумма (сложение) по
модулю 2
(другие названия суммы по модулю 2: операция «неравнозначно»,
«исключающее ИЛИ», «разность»). Формула, построенная из констант 0, 1, от-
дельных переменных, их конъюнкций или сумм по модулю 2, называется поли-
номом Жегалкина
[57, с. 32].
Аксиомы для конъюнкции даны в параграфе 4.2, поэтому приведём лишь
аксиомы, относящиеся к операции сложения по модулю 2:
;
0
0
0
=
⊕
(6.3)
;
1
1
0
=
⊕
(6.4)
;
1
0
1
=
⊕
(6.5)
,
0
1
1
=
⊕
(6.6)
где знак ⊕ обозначает операцию суммы по модулю 2.

133
При помощи аксиом легко найти значение любого выражения Жегалкина,
если заданы значения аргументов. Вычислим, например, значение выражения
AC
BC
A
⊕
⊕
(6.7)
на наборе 101. Так как согласно набору 101 A = 1, B = 0, C = 1, то
1 0 1 1 1 1 0 1 1 1 0.
⊕ ⋅ ⊕ ⋅ = ⊕ ⊕ = ⊕ =
Таким образом, выражение (6.7) на наборе 101 равно нулю.
Операция суммы по модулю 2 коммутативна и ассоциативна:
;
A
B
B
A
⊕
=
⊕
),
(
)
(
C
B
A
C
B
A
⊕
⊕
=
⊕
⊕
что позволяет записывать подобные выражения без скобок и в любом порядке:
.
)
(
)
(
D
C
A
B
D
C
B
A
D
C
B
A
⊕
⊕
⊕
=
⊕
⊕
⊕
=
⊕
⊕
⊕
Справедливость свойств коммутативности и ассоциативности легко дока-
зать при помощи аксиом (6.3)–(6.6).
В алгебре Жегалкина конъюнкция дистрибутивна относительно суммы по
модулю 2:
,
)
(
AC
AB
C
B
A
⊕
=
⊕
что позволяет раскрывать скобки и выносить за скобки как отдельные перемен-
ные, так и любые выражения.
Но сумма по модулю 2 не дистрибутивна относительно конъюнкции
).
)(
(
C
A
B
A
C
B
A
⊕
⊕
≠
⊕
Основные соотношения, связывающие операции булевой алгебры с опе-
рациями алгебры Жегалкина, имеют вид:
;
B
A
B
A
B
A
+
=
⊕
(6.8)
.
AB
B
A
B
A
⊕
⊕
=
+
(6.9)
Из этих формул выводятся следующие важные частные случаи:
а) пусть B = 1, тогда из формулы (6.8) получаем:
,
1 A
A
=
⊕
(6.10)
т. е. инверсия некоторого булева выражения в алгебре Жегалкина представля-
ется как сумма по модулю 2 этого выражения и единицы;
б) из формулы (6.9) следует, что если f
1
f
2
= 0, то
f
1
+ f
2
= f
1
⊕ f
2
,
(6.11)
где f
1
и f
2
– некоторые логические выражения.
в) пусть f
1
= f
2
, тогда
f
1
⊕ f
1
= 0.
(6.12)

134
С помощью формул (6.8)–(6.12) всякое булево выражение можно пред-
ставить полиномом Жегалкина, и наоборот, всякий полином Жегалкина можно
перевести в булеву алгебру.
6.5 Упрощение логических выражений в алгебре Жегалкина
Упрощение формул в алгебре Жегалкина осуществляется в основном с
помощью соотношения (6.12).
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.9
· · · · · · · · · · · · · · · · · · · · · · ·
Представить в алгебре Жегалкина булево выражение
.
C
A
AB
f
+
=
Поскольку
,
0
=
⋅ C
A
AB
то, согласно (6.11),
.
C
A
AB
C
A
AB
f
⊕
=
+
=
С применением формулы (6.10) получаем:
.
)
1
(
C
AC
AB
C
A
AB
C
A
AB
f
⊕
⊕
=
⊕
⊕
=
⊕
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.10
· · · · · · · · · · · · · · · · · · · · · ·
Представить в алгебре Жегалкина булево выражение
.
f
AB
BC
=
+
В этом выражении конъюнкция слагаемых не равна нулю:
,
0
≠
⋅ BC
AB
следовательно, по формуле (6.9):
.
ABC
BC
AB
BC
AB
f
⊕
⊕
=
+
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.11
· · · · · · · · · · · · · · · · · · · · · ·
Представить в булевой алгебре выражение Жегалкина
.
ABC
BC
AC
AB
f
⊕
⊕
⊕
=
Вынесем за скобки AB и аргумент C:
).
(
)
(
)
1
(
B
A
C
C
AB
B
A
C
C
AB
f
⊕
⊕
=
⊕
⊕
⊕
=
Согласно выражению (6.8), получаем:
.)
(
)
(
)
(
BC
A
C
B
A
C
AB
B
A
B
A
C
C
AB
B
A
C
C
AB
f
+
⊕
=
+
⊕
=
⊕
⊕
=

135
Заметим, что
,
0
)
(
=
+
⋅
BC
A
C
B
A
C
AB
т. е. конъюнкция слагаемых равна нулю, следовательно, по формуле (6.11) по-
лучаем искомый результат:
.
BC
A
C
B
A
C
AB
f
+
+
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.12
· · · · · · · · · · · · · · · · · · · · · ·
Упростить в алгебре Жегалкина:
.
AC
AB
ABC
BC
ABC
BC
ABC
AB
f
⊕
⊕
⊕
⊕
⊕
⊕
⊕
=
В этом выражении два раза встречается конъюнкция AB, два раза – конъ-
юнкция BC и три раза – конъюнкция ABC. Согласно формуле (6.12), получаем:
.
;
0
;
0
ABC
ABC
ABC
ABC
BC
BC
AB
AB
=
⊕
⊕
=
⊕
=
⊕
С учётом этих значений искомая минимальная форма имеет вид
.
AC
ABC
f
⊕
=
Всякое выражение Жегалкина можно представить в СДНФ. Для этого
каждую конъюнкцию заменяем дизъюнкцией соответствующих минтермов, по-
сле чего все знаки дизъюнкции заменяем знаками суммы по модулю 2. После
этого удаляем пары одинаковых минтермов.
Например, представим в СДНФ полином Жегалкина:
.
)
,
,
(
C
AC
AB
C
B
A
f
⊕
⊕
=
(6.13)
Запишем каждую из конъюнкций полинома (6.13) в виде дизъюнкции
минтермов:
.
;
;
ABC
C
B
A
BC
A
C
B
A
C
ABC
C
B
A
AC
ABC
C
AB
AB
⊕
⊕
⊕
=
⊕
=
⊕
=
Их сумма по модулю 2 имеет вид:
.
ABC
C
B
A
BC
A
C
B
A
ABC
C
B
A
ABC
C
AB
f
⊕
⊕
⊕
⊕
⊕
⊕
⊕
=
Упростим это выражение, применяя свойство (6.12):
).
7
,
6
,
3
,
1
(
=
⊕
⊕
⊕
=
ABC
C
AB
BC
A
C
B
A
f
(6.14)
Найти СДНФ полинома Жегалкина можно и с помощью карты Вейча.
Карта приведена на рисунке 6.21. Наносим на неё конъюнкцию AB, поставив
единицы в клетках, относящихся к минтермам 6 и 7. Затем наносим конъюнк-
цию AC, поставив единицы в клетках минтермов 5 и 7. При этом в клетке мин-