ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16673
Скачиваний: 202
136
терма 7 окажется две единицы. Точно так же наносим на карту переменную C,
поставив единицы в клетках минтермов 1, 3, 5 и 7. Клетки, в которых стоят две
единицы, говорят о том, что соответствующие минтермы необходимо удалить.
На рисунке 6.21 это клетка минтерма 5. Удаляем две единицы и из клетки мин-
терма 7. В результате получится карта, приведённая на рисунке 6.22. Согласно
этой карте,
f = (1, 3, 6, 7),
что полностью соответствует выражению (6.14), найденному путём алгебраиче-
ских преобразований.
Подробности об алгебре Жегалкина можно найти в [55].
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Найдите значения следующих выражений:
1)
0
1
1
1
⊕
⊕
⊕
,
1
1
0
0
⊕
⊕
⊕
,
0
1
1
⊕
⊕
;
2)
0
1
0
1
⊕
⊕
⊕
,
0
1
1
1
⊕
⊕
⊕
,
1
1
0
⊕
⊕
.
2.
Укажите значения следующих выражений, если A = B = 1,
C = 0:
1)
C
B
A
⊕
⊕
,
C
AB ⊕
,
B
AC ⊕
;
2)
,
AВ
C
B
⊕
⊕
,
AB
ABC ⊕
.
ABC
AB
A
⊕
⊕
3.
Упростите в алгебре Жегалкина:
1)
;
BC
AB
BC
BC
AB
BC
ABC
f
⊕
⊕
⊕
⊕
⊕
⊕
=
2)
;
)
)(
(
ABC
AC
ABC
AC
BC
B
A
f
⊕
⊕
⊕
⊕
⊕
=
3)
;
)
)(
(
ABC
AC
AB
B
A
f
⊕
⊕
⊕
=
4)
.
)
)(
(
AB
BC
AB
BC
AB
AC
f
⊕
⊕
⊕
⊕
=
4.
Представьте булево выражение в алгебре Жегалкина и
упростите:
1)
;
C
B
A
C
B
A
C
B
A
ABC
f
+
+
+
=
2)
;
f
ABC
AC
ABC
=
+
+
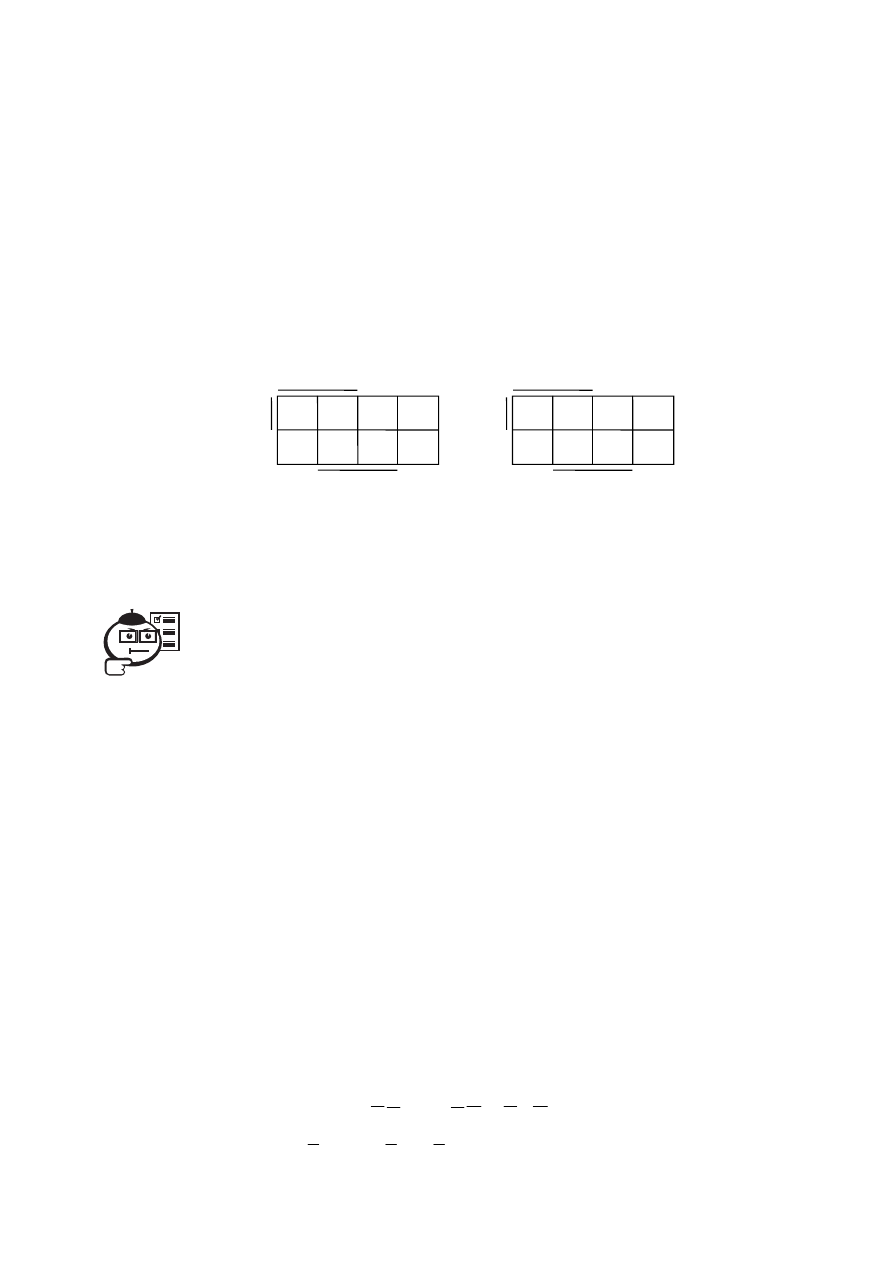
Рис. 6.21
A
B
C
1
1
11 1
111
Рис. 6.22
A
B
C
1
1
1 1

137
3)
;
C
B
A
BC
A
C
B
A
C
AB
f
+
+
+
=
4)
.
f
ABC
ABD
ACD
BCD
=
+
+
+
5.
Найдите минимальные ДНФ в булевой алгебре по задан-
ным выражениям Жегалкина:
1)
;
)
1
(
BC
C
AB
A
B
f
⊕
⊕
⊕
⊕
=
2)
;
ABC
AC
BC
C
A
f
⊕
⊕
⊕
⊕
=
3)
.
1
⊕
⊕
⊕
=
ABC
AC
C
f
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
6.6 Производная от булевой функции
Производная по переменной A от булевой функции
)
,
,
,
(
L
B
A
f
…
показы-
вает, при каких условиях изменение аргумента A вызывает изменение значения
функции
)
,
,
,
(
L
B
A
f
…
. Например, функция
BC
A
C
B
A
f
+
=
)
,
,
(
меняет своё значение одновременно с аргументом A в следующих трёх случаях:
а)
если B = C = 0;
б)
если B = 0; C = 1;
в)
если B = 1; C = 0.
Эти три случая удобно представить в виде булевой функции ( , )
B C
ϕ
:
( , )
.
B C
B
C
ϕ
=
+
Функция ( , )
B C
ϕ
обладает важным свойством. При ( , ) 1
B C
ϕ
= функция
( , , )
f A B C
меняет свои значения одновременно с изменением значения аргу-
мента A.
Функцию
( ,
, )
B
L
ϕ
…
называют производной по переменной A от булевой
функции
)
,
,
,
(
L
B
A
f
…
и обозначают:
( ,
, ).
f
B
L
A
∂
= ϕ
∂
…
Рассмотрим ещё один пример. Найдем производную по переменной А:
D
C
A
D
C
B
D
B
A
B
A
f
+
+
+
=
.
(6.15)
Подставим в это выражение какой-либо набор значений аргументов B, C,
D. Получим один из четырех результатов:
f = 1; f = 0; f = А; f = A .
Все наборы, на которых f = А или f = A , образуют функцию φ(B, C, D).

138
Найдем функцию
( , , )
B C D
ϕ
. Для этого в (6.15) подставим все наборы
значений переменных B, C, D и для каждого набора найдем остаточную функ-
цию:
( , 0, 0, 0)
0
0 0 0 0 0
0 0
;
f A
А
А
А
А
= ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =
( , 0, 0,1)
0
0 1 0 0 1
0 1
;
f A
А
А
А
А
= ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =
( , 0,1, 0)
0
0 0 0 1 0
1 0 0;
f A
А
А
А
= ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =
( , 0,1,1)
0
0 1 0 1 1
1 1 1;
f A
А
А
А
= ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =
( , 1, 0, 0)
1
1 0 1 0 0
0 0
;
f A
А
А
А
А
= ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =
( ,1, 0,1)
1
1 1 1 0 1
0 1
;
f A
А
А
А
А
= ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =
( ,1,1, 0)
1
1 0 1 1 0
1 0
;
f A
А
А
А
А
= ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =
( , 1,1,1)
1
1 1 1 1 1
1 1
.
f A
А
А
А
А
= ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =
Функция f равна А или A на шести наборах значений переменных B, C, D.
Это наборы 0, 1, 4, 5, 6, 7. Дизъюнкция соответствующих минтермов является
искомой производной:
( , , ) (0,1, 4, 5, 6, 7).
f
B C D
A
∂
= ϕ
=
∂
Если ее минимизировать, то получим:
C
B
A
f
+
=
∂
∂
.
Найти производную
A
f
∂
∂
от функции
)
,
,
,
(
L
B
A
f
…
можно и аналитическим
путём. Согласно [14], производная первого порядка
A
f
∂
∂
от функции
)
,
,
,
(
L
B
A
f
…
записывается в виде
),
,
,
,
0
(
)
,
,
,
1
(
L
B
f
L
B
f
A
f
…
…
⊕
=
∂
∂
(6.16)
где
)
,
,
,
1
(
L
B
f
…
– единичная остаточная функция, получающаяся на основе
функции
),
,
,
,
(
L
B
A
f
…
если в ней все вхождения аргумента A заменить едини-
цами. При этом все логические операции – И, ИЛИ, НЕ – остаются неизменны-
ми;
)
,
,
,
0
(
L
B
f
…
– нулевая остаточная функция, получающаяся на основе
функции
),
,
,
,
(
L
B
A
f
…
если в ней все вхождения аргумента A заменить нулями.

139
Согласно (6.8) выражение (6.16) записывается в булевой алгебре (т. е. без
знака «⊕») следующим образом:
.)
,
,
,
0
(
)
,
,
,
1
(
)
,
,
,
0
(
)
,
,
,
1
(
L
B
f
L
B
f
L
B
f
L
B
f
A
f
…
…
…
…
⋅
+
⋅
=
∂
∂
Например, найдем производную первого порядка по переменной A от
функции вида
.
D
B
BC
A
C
B
A
f
+
+
=
(1
1
) (0
0
)
(1
1
)(0
0
)
(1
1
)(0
0
)
(
) (
)
(
)(
)(
)
(
)(
)(
)
.
f
BC
BC
B D
BC
BC
B D
A
BC
BC
B D
BC
BC
B D
BC
BC
B D
BC
BC
B D
BC
B D BC
B D
BC
B D BC
B D
B C B
D BC
B D
BC
B D B C B D
BC
BCD
BC CD
∂
= ⋅
+ ⋅
+
⊕ ⋅
+ ⋅
+
=
∂
= ⋅
+ ⋅
+
⋅
+ ⋅
+
+
+ ⋅
+ ⋅
+
⋅
+ ⋅
+
=
=
+
+
+
+
+
=
=
+
+
+
+
+
+
+
=
=
+
=
+
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. Укажите десятичные наборы значений аргументов A и B, на
которых функция f = AB + C меняет свои значения с изменением ар-
гумента C.
2. Укажите десятичные наборы значений аргументов A, B, C,
на которых функция f(A, B, C, D) меняет свои значения с изменени-
ем аргумента D:
1)
;
CD
AB
f
+
=
3)
;
D
C
B
A
f
+
=
2)
;
D
C
AB
f
+
=
4)
.
D
C
B
A
f
+
=
3. Найдите минимальные ДНФ единичных остаточных функ-
ций относительно аргумента A (т. е. при A = 1):
1)
;
BC
A
BCD
ABC
f
+
+
=
3)
;
BCD
A
B
A
AB
f
+
+
=
2)
;
f
AB
AC
ABC D
=
+
+
4)
.
D
C
A
C
B
A
AB
f
+
+
=
4. Найдите минимальные ДНФ нулевых остаточных функций
(при B = 0):
1)
;
C
B
A
C
B
BC
f
+
+
=
3)
;
D
C
A
BD
C
A
f
+
+
=
2)
;
f
ABC
A BC
ABCD
=
+
+
4)
.
BD
BC
A
C
AB
f
+
+
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

140
6.7 Дифференцирование булевых функций
с применением карт Вейча
Чтобы найти производную при помощи карты Вейча, достаточно нанести
на неё остаточные функции дифференцируемой функции.
При этом необходимо иметь в виду, что остаточные функции представле-
ны в булевой алгебре, а сами они соединены знаком сложения по модулю 2.
Следовательно, единичная остаточная функция наносится на карту Вейча так,
как это делается в булевой алгебре, т. е. в каждой клетке указывается не более
одной единицы. Нулевая остаточная функция наносится аналогично. В резуль-
тате в каждой клетке будут либо две единицы, либо одна, либо ни одной. Если в
какой-либо клетке стоят две единицы, то заменяем их нулями. В результате по-
лучим СДНФ искомой производной.
Можно воспользоваться и тремя картами Вейча: на первые две нанести
единичную и нулевую остаточные функции, поставив между ними знак сложе-
ния по модулю 2, а на третью – результат суммирования по модулю 2. Поясним
это на примере. Найдём производную по переменной A от функции
.
CD
B
BD
A
C
A
AB
f
+
+
+
=
Остаточные функции имеют вид:
(1, , , )
;
(0, , , )
.
f
B C D
B
BCD
f
B C D
C
BD
BCD
= +
= +
+
Запишем производную в виде суммы по модулю 2 остаточных функций:
(
)
(
).
f
B
BCD
C
BD
BCD
A
∂
=
+
⊕
+
+
∂
Единичную остаточную функцию нанесём на первую карту Вейча
(рис. 6.23), нулевую – на вторую. Между ними поставим знак «⊕». Справа рас-
положим третью карту. На ней запишем СДНФ искомой производной. Её ми-
нимальная форма имеет вид:
.
D
C
B
D
C
B
A
f
+
=
∂
∂
B
C
D
1
1
1
1
1
Рис. 6.23
B
C
D
1
1
1 1
B
C
D
1
1
⊕
=
1