ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16679
Скачиваний: 202

126
28.
f
AC
ADE
AB
CDE
=
+
+
+
(рис. 5.94).
Рис. 5.93
1
1
1 ×
× × 1
×
1
×
1 × ×
1 1
×
Рис. 5.94
1 1
×
× ×
1 1 ×
× 1 × ×
1
×
× ×
1
1 1
×
× 1 ×

127
6 Конъюнктивные формы и другие направления
в развитии булевой алгебры
6.1 Минимизация конъюнктивных
нормальных форм булевых функций
Всякая булева функция может быть представлена не только в ДНФ, но и
в КНФ. В данном параграфе рассмотрим приём, позволяющий на основе ДНФ
заданной функции f найти её КНФ. Суть его состоит в двойном инвертировании
выражения f. Первое инвертирование осуществляется на уровне СДНФ.
В результате получается инверсия исходного выражения, состоящая из всех
минтермов, отсутствующих в заданной функции. Затем инверсию минимизиру-
ем и её минимальную ДНФ инвертируем по теореме де Моргана.
Например, пусть требуется найти минимальную КНФ следующей функ-
ции четырёх аргументов:
.
D
ABC
D
B
A
BCD
A
D
C
A
f
+
+
+
=
СДНФ её инверсии имеет вид:
(0, 1, 2, 3, 5, 9,10,11,13,15).
f =
Воспользовавшись картой Вейча, получаем минимальную ДНФ для
:
f
.
f
AD
CD
BC
A B
=
+
+
+
(6.1)
Инвертируем это выражение и получаем минимальную КНФ:
.)
)(
)(
)(
(
B
A
C
B
D
C
D
A
f
+
+
+
+
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Сколько знаков дизъюнкции и сколько вхождений пере-
менных в минимальных КНФ следующих функций четырёх пере-
менных?
1)
;
D
B
A
D
B
A
C
B
A
CD
A
D
C
B
f
+
+
+
+
=
2)
;
D
C
A
D
B
A
C
B
A
ABC
D
AB
f
+
+
+
+
=
3)
;
D
C
B
A
D
C
B
A
C
A
ABCD
D
B
f
+
+
+
+
=
4)
;
D
C
B
A
D
C
B
A
CD
A
D
C
AB
f
+
+
+
=
5)
.
D
C
B
A
D
C
B
A
BCD
A
D
C
A
f
+
+
+
=

128
2.
Сколько знаков дизъюнкции и сколько вхождений пере-
менных в минимальных КНФ следующих функций четырёх пере-
менных?
1)
;
)
)(
)(
)(
)(
(
D
B
A
D
B
A
C
B
A
D
C
A
D
C
B
f
+
+
+
+
+
+
+
+
+
+
=
2)
;
)
)(
)(
)(
)(
(
D
C
A
D
B
A
C
B
A
C
B
A
D
B
A
f
+
+
+
+
+
+
+
+
+
+
=
3)
;
)
)(
)(
)(
)(
(
D
C
A
D
B
C
B
A
C
B
A
D
B
A
f
+
+
+
+
+
+
+
+
+
=
4)
;
)
)(
)(
)(
)(
(
D
C
A
D
B
A
C
B
C
B
A
D
A
f
+
+
+
+
+
+
+
+
=
5)
.)
)(
)(
)(
)(
(
D
C
B
D
B
A
D
B
A
C
B
A
D
A
f
+
+
+
+
+
+
+
+
+
=
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
6.2 Минимизация КНФ с учётом неопределённых состояний
Минимизация КНФ с учётом неопределённых состояний при помощи
карт Вейча осуществляется следующим образом:
а)
наносим на карту Вейча заданную функцию f;
б)
наносим на эту же карту неопределённые состояния (если в одной и
той же клетке окажутся единица и неопределённость, то ставим не-
определённость);
в)
строим карту Вейча для инверсии заданной функции
f
. Для этого на
ней вместо нулей ставим единицы, а вместо единиц – нули;
г)
находим минимальную ДНФ функции
f
;
д)
минимальную ДНФ функции
f
инвертируем по теореме де Моргана.
Получим минимальную КНФ.
Например, найдём минимальную КНФ функции четырёх аргументов:
),
12
,
11
,
9
,
4
,
1
(
=
f
не определённой на состояниях 0, 5, 7, 8, 13, 15.
На рисунке 6.1 изображена карта Вейча для заданной функции. Крести-
ками на ней отмечены неопределённые состояния. На рисунке 6.2 приведена
карта Вейча, на которую нанесена инверсия заданной функции с теми же не-
определёнными состояниями. (Неопределённые состояния не инвертируются,
они остаются неопределёнными независимо от того, в какой форме записывает-
ся функция – ДНФ, КНФ или в какой-либо из форм высшего порядка.)

129
Анализируем карту (рис. 6.2). На ней имеется одна единица (минтерм 3),
которая даёт единственным образом простую импликанту
,
C
A
если на наборе
0111 (десятичное 7) функцию
f
доопределить единицей. Оставшиеся две еди-
ницы (минтермы 10 и 14) вместе с соседними минтермами 2 и 6 дают ещё одну
простую импликанту
.
D
C
Таким образом, получаем:
.
f
AC
CD
=
+
Инвертируем это выражение и получаем минимальную КНФ:
).
)(
(
D
C
C
A
f
+
+
=
Чтобы из КНФ функцию перевести в ДНФ, в ней можно раскрыть скобки
и полученный результат представить в ДНФ (совершенной или минимальной).
Например, представим в минимальной ДНФ функцию
).
)(
)(
)(
(
C
B
A
C
B
D
C
C
A
f
+
+
+
+
+
=
(6.2)
Раскрываем скобки:
(
)(
)(
)
(
)(
)
.
f
AC
AD C D B C A
B
C
ABC
ABD
BC D
AC D C D A
B
C
ABC D
AC D
ABC D
BC D
ABC
ABCD
=
+
+
+
+ +
=
=
+
+
+
+
+ +
=
=
+
+
+
+
+
Наносим это выражение на карту Вейча (рис. 6.3) и минимизируем:
.
ABC
D
C
B
D
C
A
f
+
+
=
Функцию (6.2) можно перевести в ДНФ и другим способом. Сначала по
теореме де Моргана находим её инверсию:
.
f
AC
CD
BC
ABC
=
+
+
+
Инверсию наносим на карту Вейча (рис. 6.4). Инвертируем карту, полу-
чим прямую форму, представленную в СДНФ (рис. 6.3). А на основе СДНФ не-
трудно найти любую другую ДНФ.
Рис. 6.1
1
1
× × × ×
1 1
1
×
×
Рис. 6.2
1
1
× × × ×
1
× 1 1 ×
Рис. 6.3
1
1
1
1
1
Рис. 6.4
1
1
1
1 1
1 1 1 1
1 1
130
6.3 Примеры минимизации КНФ
с учётом неопределённых состояний
Как и в случае дизъюнктивных нормальных форм булевых функций, ми-
нимизация конъюнктивных форм с учётом неопределённых состояний нередко
осуществляется неоднозначно. Но в данном параграфе приводятся только по
одной минимальной форме для каждой функции.
( , , ) (1, 3, 5, 7);
f A B C =
[0, 4, 6].
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.1
· · · · · · · · · · · · · · · · · · · · · · ·
На рисунках 6.5 и 6.6 приведены СДНФ функции
( , , ) (1, 3, 5, 7);
f A B C =
[0, 4, 6],
и её инверсии. Минимальная ДНФ инверсии имеет вид
;
f
C
=
минимальная
КНФ: f = C.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.2
· · · · · · · · · · · · · · · · · · · · · · ·
На рисунке 6.7 представлена СДНФ функции
( , , ) (3, 5, 7);
f A B C =
[2, 4, 6].
На рисунке 6.8 – СДНФ её инверсии. Минимальная ДНФ инверсии:
;
f
AB
=
минимальная КНФ:
f
A
B
= +
.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 6.3
· · · · · · · · · · · · · · · · · · · · · · ·
( , , ) (1, 5, 7);
f A B C =
[0, 6].
На рисунке 6.9 приведена СДНФ; на рисунке 6.10 – СДНФ инверсии.
Минимальная ДНФ инверсии:
;
f
AB
С
=
+
минимальная КНФ:
(
) .
f
A
B С
=
+
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
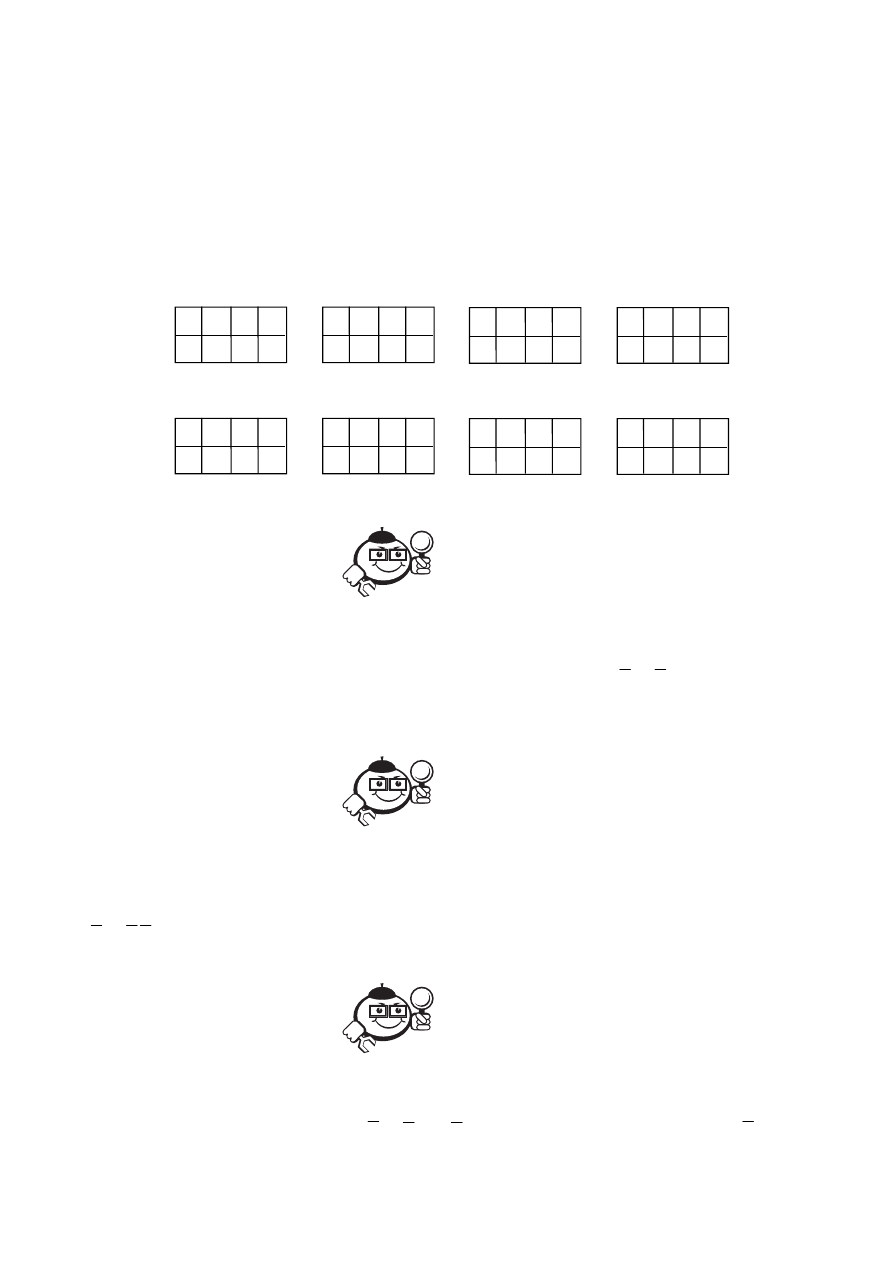
Рис. 6.5
×
×
1
1
×
1
× 1
×
1
×
×
1
×
×
1
× 1
×
1
1
×
Рис. 6.6
Рис. 6.7
Рис. 6.8
Рис. 6.9
× 1
×
1
1
1
1
×
×
1
1
×
1
×
1
× 1
×
1
1
Рис. 6.10
Рис. 6.12
Рис. 6.11