ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16668
Скачиваний: 202
146
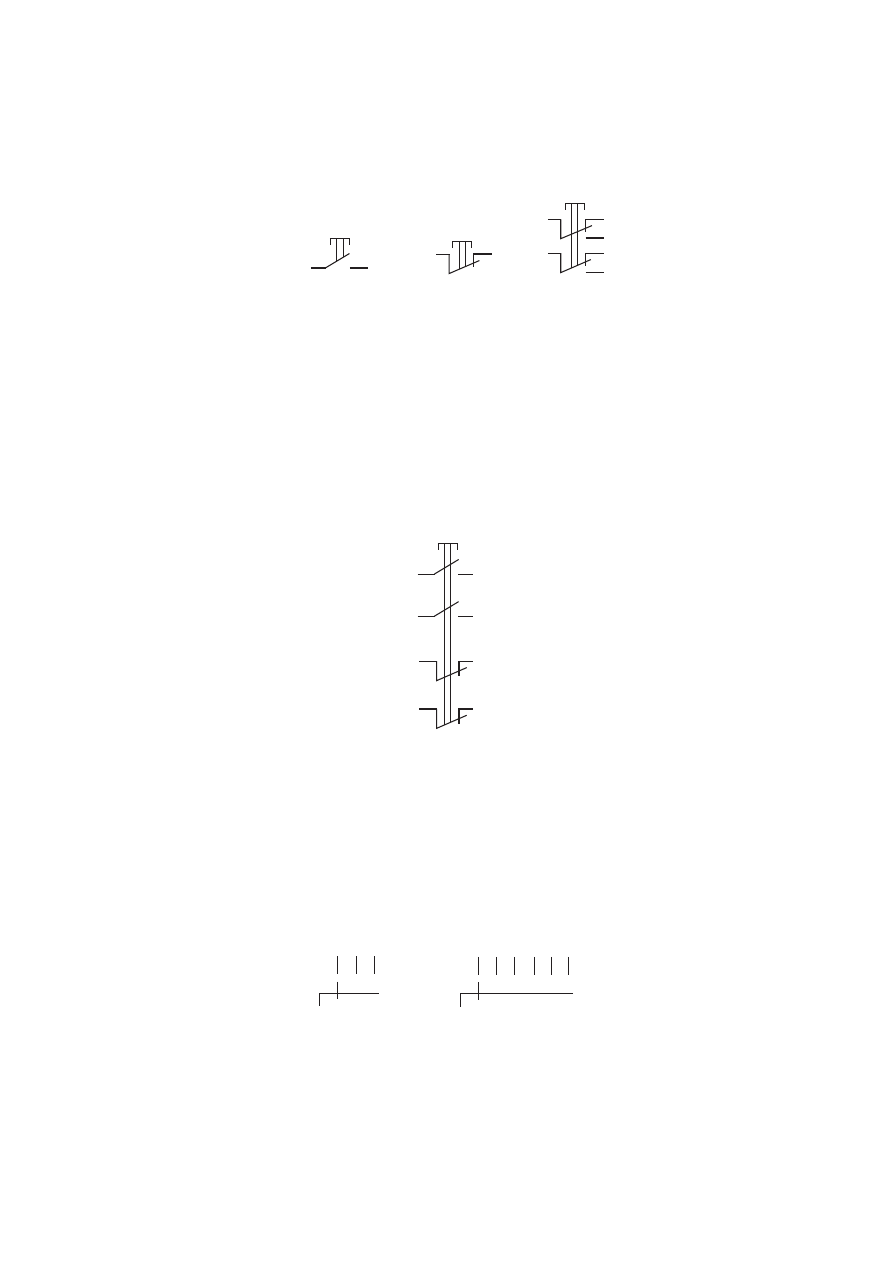
m и k соединены. Если же кнопку нажать, то между ними не будет проводимо-
сти. После отпускания кнопки выводы m и k соединятся снова. На рисунке 7.2,
в приведена кнопка с двумя группами переключательных контактов.
Рис. 7.2
В общем случае одна и та же кнопка может объединять в своей конструк-
ции несколько нормально разомкнутых и несколько нормально замкнутых кон-
тактов. Пример такой кнопки приведен на рисунке 7.3. Если её нажать, то все
нормально разомкнутые контакты замкнутся, а все нормально замкнутые разо-
мкнутся. При отпускании кнопки все контакты вернутся в исходное состояние.
Рис. 7.3
Кроме кнопок и тумблеров, изображённых на рисунках 7.1–7.3, в технике
применяются и многопозиционные переключатели. Например, на рисунке 7.4, а
показан трёхпозиционный переключатель, а на рисунке 7.4, б – шестипозици-
онный.
Рис. 7.4
7.4 Электромагнитные реле
Ещё одним контактным элементом, получившим широчайшее примене-
ние в промышленности, является электромагнитное реле. Его схематическое
а)
б)
в)
m
n
m
k
a
c
e
k
b
d
f
m
а)
1
б)
2 3
1 2 3 4 5 6
147
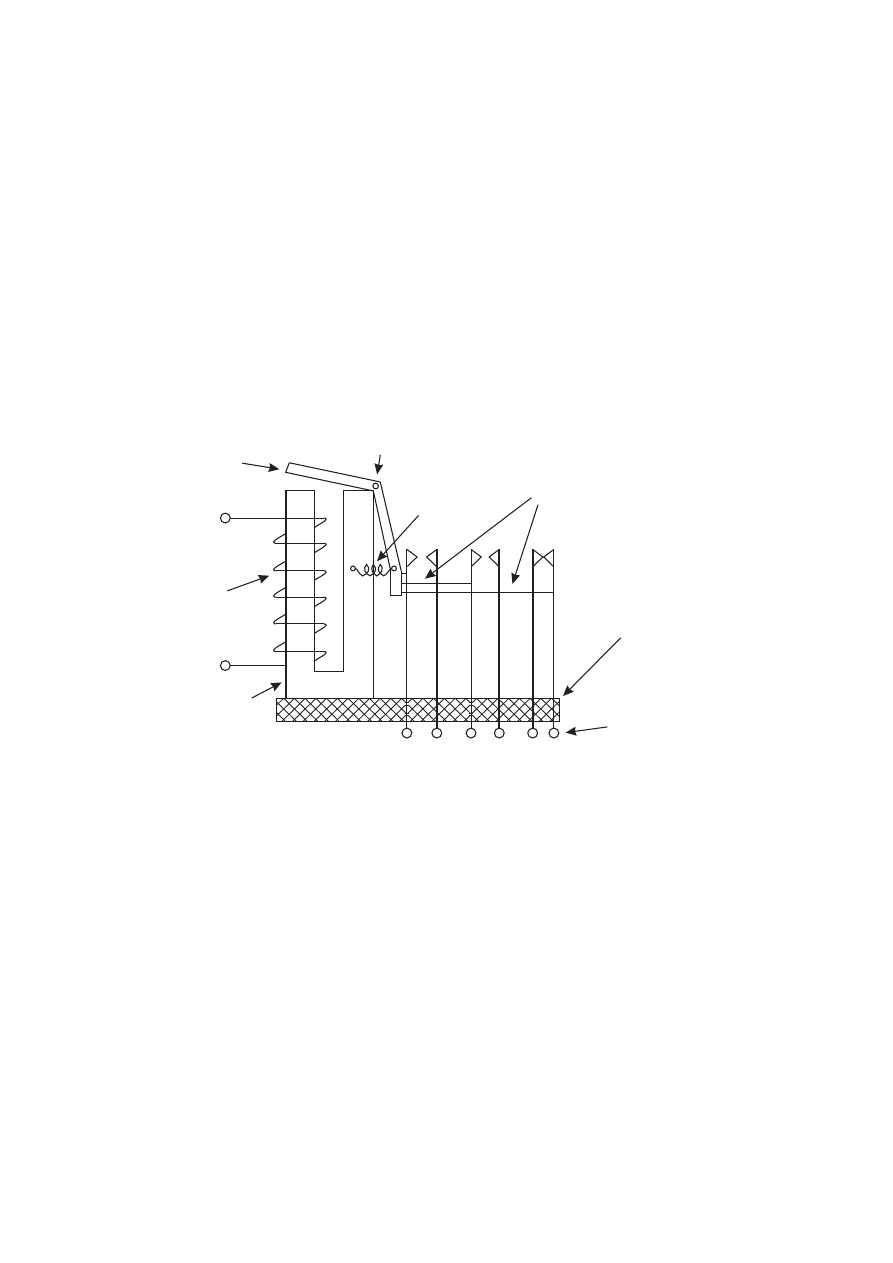
изображение представлено на рисунке 7.5. Изменение состояния контактов реле
вызывается электрическим током, подаваемым на обмотку электромагнита,
имеющегося у каждого реле. На рисунке 7.5 обмотка показана несколькими
витками. Реальные же реле содержат, как правило, сотни и тысячи витков тон-
кой медной проволоки, покрытой слоем какого-либо диэлектрика. Под дей-
ствием протекающего по обмотке тока стальной сердечник превращается в
электромагнит, который притягивает якорь, изготовленный также из стали.
Якорь, поворачиваясь вокруг оси, через диэлектрические штанги отклоняет по-
движные упругие контактные пластины (выводы 1 и 3 на рис. 7.5) и замыкает
их с неподвижными пластинами 2 и 4.
Рис. 7.5
Пара контактных пластин 5 и 6 при выключенном реле находится в за-
мкнутом состоянии. Если по обмотке пропустить ток, то якорь отклонит по-
движную пластину 6 и контактная пара разомкнётся. При отключении тока
якорь под действием возвратной пружины приходит в исходное состояние.
Условное изображение электромагнитного реле показано на рисунке 7.6,
где прямоугольником обозначена обмотка электромагнита. Реле на этом рисун-
ке содержит два нормально разомкнутых контакта, один нормально замкнутый
и одну переключательную группу.
1
2
3 4
5 6
Выводы
контактных
пластин
Электромагнит
(неподвижный
сердечник)
Обмотка
(электрическая
катушка)
Якорь
(подвижный
сердечник)
Ось
поворота
Возвратная
пружина
Диэлектрические
штанги,
отклоняющие
контактные
пластины
Диэлектрическая мон-
тажная колодка, на
которой укреплены
электромагнит и кон-
тактные пластины

148
Рис. 7.6
7.5 Контактная интерпретация булевых формул
Интерпретация (лат. interpretation – разъяснение, истолкование) – это
приписывание символам и формулам формальной системы определенного со-
держания, смысла, значения. Пусть множество параллельно-последовательных
контактных структур образует систему A, а множество аналитически заданных
булевых функций произвольного порядка образует систему B. Рассмотрим от-
ношения между элементами систем A и B и их интерпретацию.
Если логический аргумент принимает единичное значение, то нормально
разомкнутый контакт соответствующего реле замкнут (а нормально замкну-
тый – разомкнут). И наоборот: если нормально разомкнутый контакт реле за-
мкнут (а нормально замкнутый – разомкнут), то соответствующий логический
аргумент принимает единичное значение.
Если логический аргумент принимает нулевое значение, то нормально
разомкнутый контакт соответствующего реле разомкнут (а нормально замкну-
тый – замкнут). И наоборот: если нормально разомкнутый контакт реле разо-
мкнут (а нормально замкнутый – замкнут), то соответствующий логический ар-
гумент принимает нулевое значение.
Аналогично интерпретируются функции: если булева функция равна ну-
лю, то соответствующая контактная цепь разомкнута. И наоборот, если цепь
разомкнута, то соответствующая булева функция равна нулю. Если булева
функция равна единице, то соответствующая цепь контактов замкнута.
И наоборот, если цепь замкнута, то соответствующая булева функция принима-
ет единичное значение.
Между элементами системы A существуют отношения: контакты могут
соединяться параллельно или последовательно. Отношения между элементами
системы B: логические переменные могут соединяться знаками конъюнкции
или дизъюнкции. В этом случае имеет место интерпретация: логическая опера-
149
ция дизъюнкции обозначает параллельное соединение контактов, и наоборот,
параллельному соединению контактов соответствует операция дизъюнкции.
Конъюнкция обозначает последовательное соединение контактов, и последова-
тельному соединению контактов соответствует операция конъюнкции.
Таким образом, формальная двоичная логическая система, ограниченная
булевыми функциями произвольного порядка, является логико-математической
моделью контактных структур параллельно-последовательного типа.
7.6 Примеры построения контактных схем
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.1
· · · · · · · · · · · · · · · · · · · · · · ·
Построить контактную схему, если булева функция имеет вид
.
D
C
B
A
f =
Функция представлена конъюнкцией четырёх переменных, среди кото-
рых переменные A и C являются нормально разомкнутыми, а остальные – нор-
мально замкнутыми. В соответствии с интерпретацией, рассмотренной в
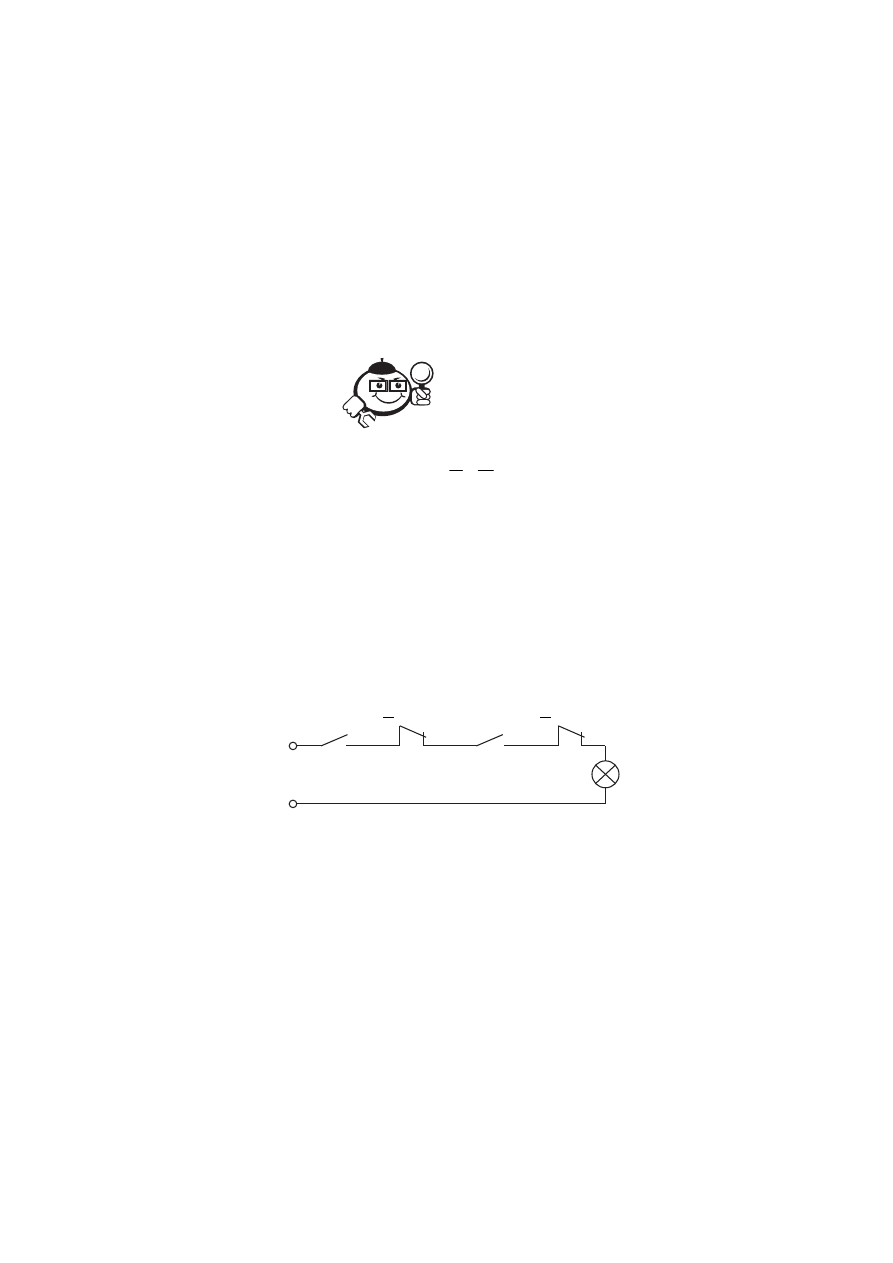
предыдущем параграфе, контакты соединяем последовательно. При этом для
определённости на схеме изобразим лампу, управляемую заданной контактной
схемой (рис. 7.7).
Рис. 7.7
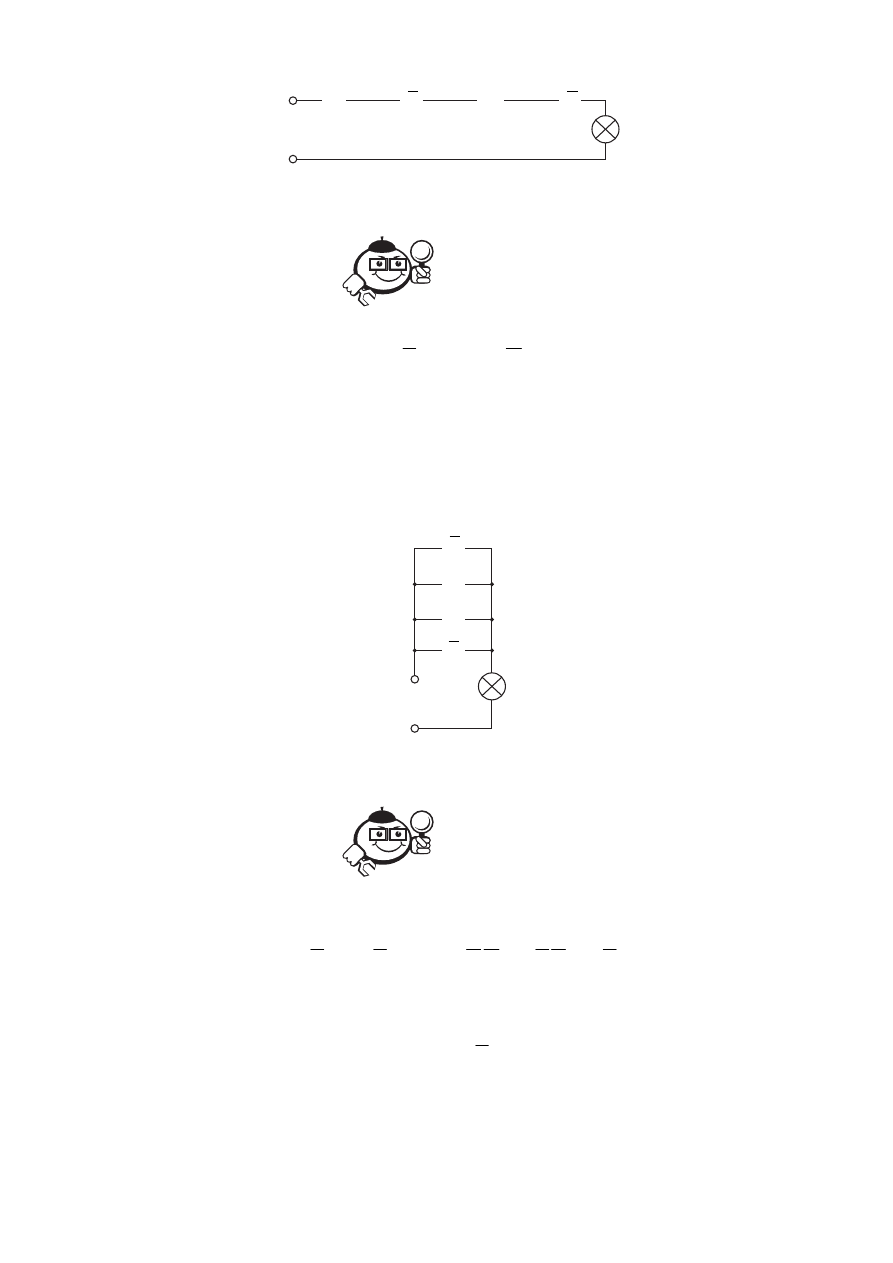
Если схема не входит в состав технической документации, то контактные
структуры могут быть представлены в упрощённом виде, без изображения кон-
тактов, так, как показано на рисунке 7.8, где приведена та же схема, что и на
рисунке 7.7. Потери информации при этом не происходит: если буква не со-
держит инверсии, то ей соответствует нормально разомкнутый контакт; ин-
версная же буква обозначает, что контакт является нормально замкнутым. Но
при изображении переключательных групп следует избегать их упрощённого
представления.
A
C
H
220 В
B
D
150
Рис. 7.8
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.2
· · · · · · · · · · · · · · · · · · · · · · ·
Построить контактную схему, если задана булева функция, имеющая вид
,
D
C
B
A
f
+
+
+
=
где логическим переменным соответствуют тумблеры с теми же обозначениями
A, B, C, D. В отличие от предыдущего случая, схема представляет собой парал-
лельное соединение контактов. Среди них два контакта не содержат инверсий
(рис. 7.9).
Рис. 7.9
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.3
· · · · · · · · · · · · · · · · · · · · · · ·
Построить контактную структуру, соответствующую ДНФ булевой
функции вида
.
E
D
C
B
A
D
C
B
A
BD
A
BC
A
f
+
+
+
+
=
Согласно этому выражению четыре цепи последовательно соединённых
контактов должны быть включены параллельно. Кроме того, в заданной функ-
ции присутствует инверсная переменная
.
E
Ей соответствует нормально за-
мкнутый контакт реле E. Его рассматриваем, как пятую цепь, представляющую
собой частный случай последовательно соединённых контактов. Таким обра-
A
C
H
220 В
B
D
B
H
220 В
A
D
C