ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16666
Скачиваний: 202
151
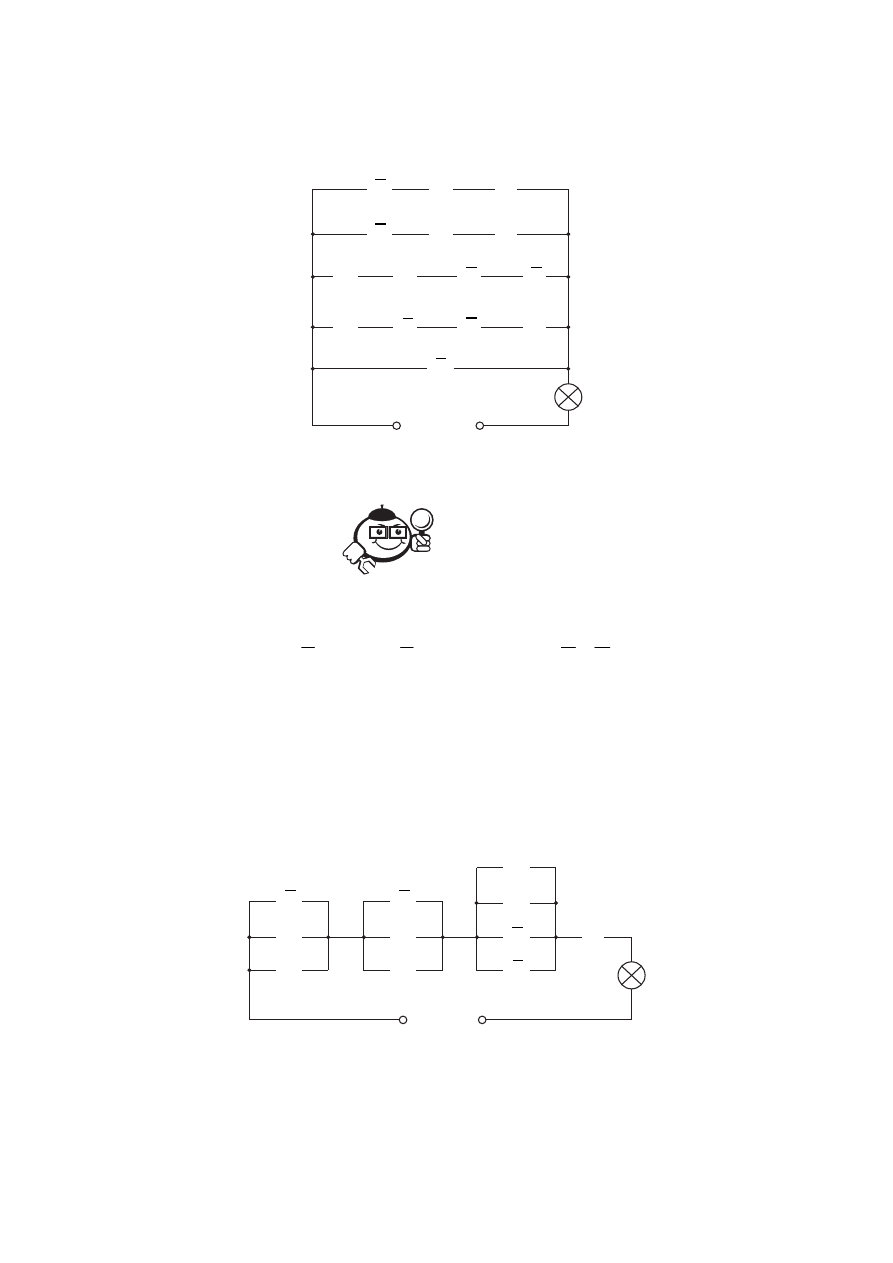
зом, согласно заданной функции контактная схема состоит из пяти параллельно
соединённых цепей (рис. 7.10).
Рис. 7.10
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.4
· · · · · · · · · · · · · · · · · · · · · · ·
Построить контактную структуру, соответствующую КНФ следующей
булевой функции:
.
)
)(
)(
(
E
D
C
B
A
D
B
A
C
B
A
f
+
+
+
+
+
+
+
=
В отличие от предыдущей схемы, моделирующей ДНФ булевой функции,
в данном случае последовательно соединяются группы параллельно соединён-
ных контактов. При этом контакт E рассматривается как частный случай груп-
пы параллельных контактных соединений, когда в группе находится лишь один
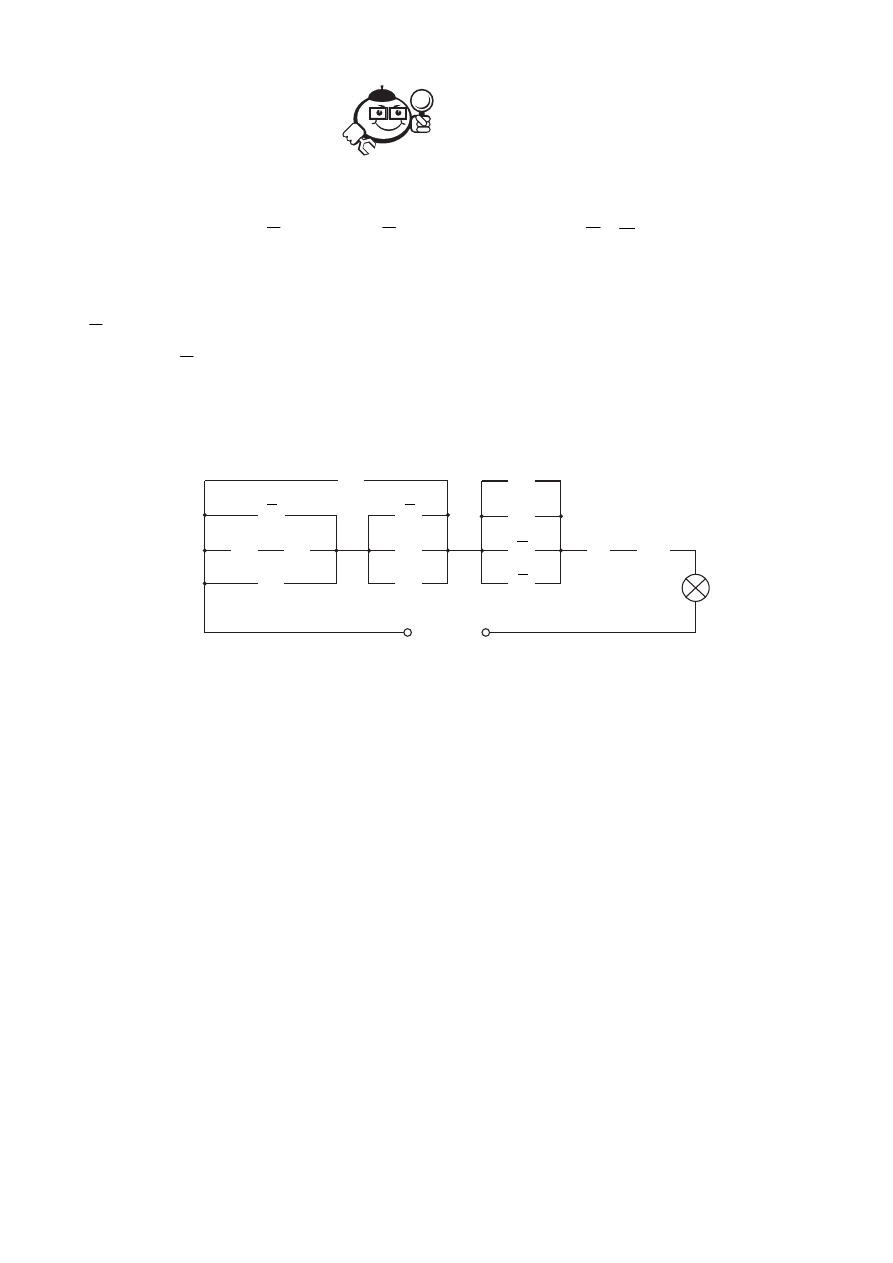
контакт. Схема приведена на рисунке 7.11.
Рис. 7.11
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
B
H
220 В
A
D
C
B
A
D
B
A
C
A
C
B
D
E
B
H
220 В
A
D
C
C
B
A
D
B
A
E
152
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.5
· · · · · · · · · · · · · · · · · · · · · · ·
Построить контактную структуру на основе булевой функции пятого по-
рядка:
.
)
](
)
)(
[(
PQ
D
C
B
A
K
E
B
A
D
BC
A
f
+
+
+
+
+
+
+
+
=
Строится схема следующим образом. Сначала последовательно соединя-
ем контакты B и C. Получившуюся цепь включаем параллельно с контактами
A и D. Затем последовательно с ними включаем параллельно соединённые
контакты ,
A B и E. Получится схема с выводами a и c (рис. 7.12). К этим точ-
кам присоединяем контакт K. Аналогично достраиваем оставшуюся часть схе-
мы.
Рис. 7.12
Анализируем получившуюся контактную структуру. Первый порядок в
заданной функции образует конъюнкция между круглыми и квадратными скоб-
ками, а также переменными P и Q. На рисунке 7.12 точка c делит схему на ле-
вую и правую части. В левой части (между точками a и c) находится схема, со-
ответствующая выражению, записанному в квадратных скобках. Согласно
этому выражению дизъюнкция между переменной K и круглыми скобками даёт
второй порядок. На рисунке 7.12 контакт K включён параллельно цепи, распо-
ложенной между точками a и c. Третий порядок образует конъюнкция между
круглыми скобками. На рисунке 7.12 это точка b. В левых круглых скобках за-
данной функции записано выражение второго порядка. Ему соответствует кон-
тактная схема на рисунке 7.12, размещённая между точками a и b.
Подобным образом можно построить контактную структуру на основе
любой булевой функции.
Отметим ещё раз, что взаимно однозначное соответствие существует
только между булевыми функциями и параллельно-последовательными кон-
тактными схемами. Если выйти в область мостиковых структур, то соответ-
C
H
220 В
A
F
D
E
B
A
E
D
B
Q
P
c
b
B
K
a
153
ствие взаимной однозначности нарушится, так как всякой мостиковой контакт-
ной структуре соответствует единственная булева функция, но для произволь-
ной булевой функции всегда можно изобразить только параллельно-
последовательную схему. А что касается мостиковых структур, то до сих пор
нет алгоритмов, позволяющих строить абсолютно экономичные мостиковые
схемы, за исключением некоторых частных случаев, например, симметриче-
ских контактных структур Клода Шеннона [23]. Следовательно, булева модель
распространяется только на параллельно-последовательные контактные струк-
туры.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
7.7 Примеры синтеза простейших контактных структур
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.6
· · · · · · · · · · · · · · · · · · · · · · ·
Дано: тумблер A с одним контактом, работающим на замыкание, и две
осветительные лампы H
1
и H
2
. Требуется соединить их так, чтобы при одном
положении тумблера горела одна лампа, а при другом – обе.
Для решения этой задачи нет необходимости привлекать булеву алгебру,
вполне достаточно обычных рассуждений. Одну лампу подключим непосред-
ственно к сетевому напряжению, а вторую – через тумблер, т. е. контакт тум-
блера соединим последовательно со второй лампой и получившуюся цепь под-
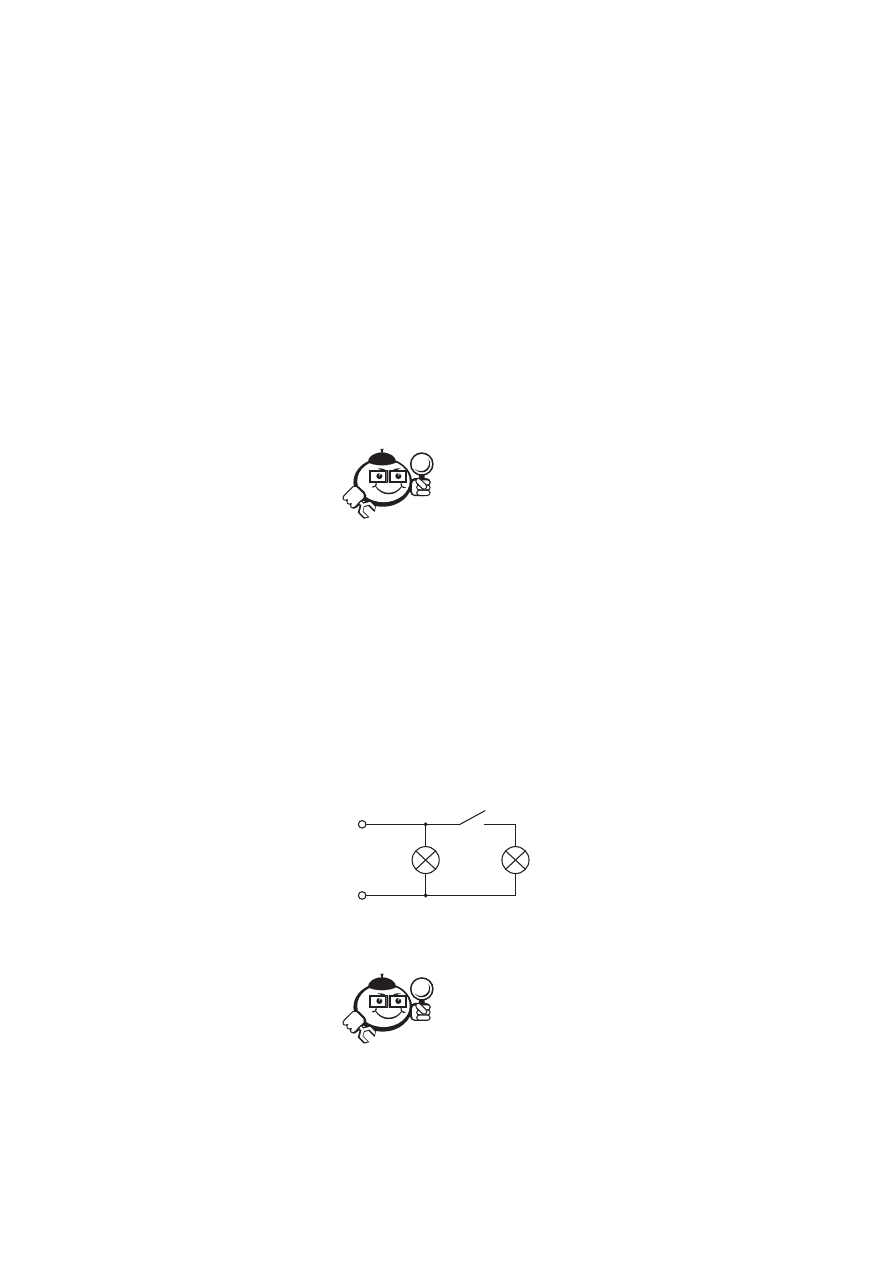
ключим к сети либо параллельно первой лампе (рис. 7.13).
Рис. 7.13
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.7
· · · · · · · · · · · · · · · · · · · · · · ·
Дано: тумблер A с одной переключательной группой контактов и три
осветительные лампы H
1
, H
2
, H
3
. Требуется подключить этот тумблер и лампы к
сетевому напряжению так, чтобы при одном положении тумблера горела толь-
ко лампа H
1
, а при другом – H
2
и H
3
. Лампа H
1
при этом гаснет.
220 В
A
H
1
H
2
154
И здесь, как и в предыдущем случае, достаточно обычных рассуждений,
т. е. вполне можно обойтись без булевой алгебры. Замкнутым контактом под-
ключим к сети лампу H
1
, а лампы H
2
и H
3
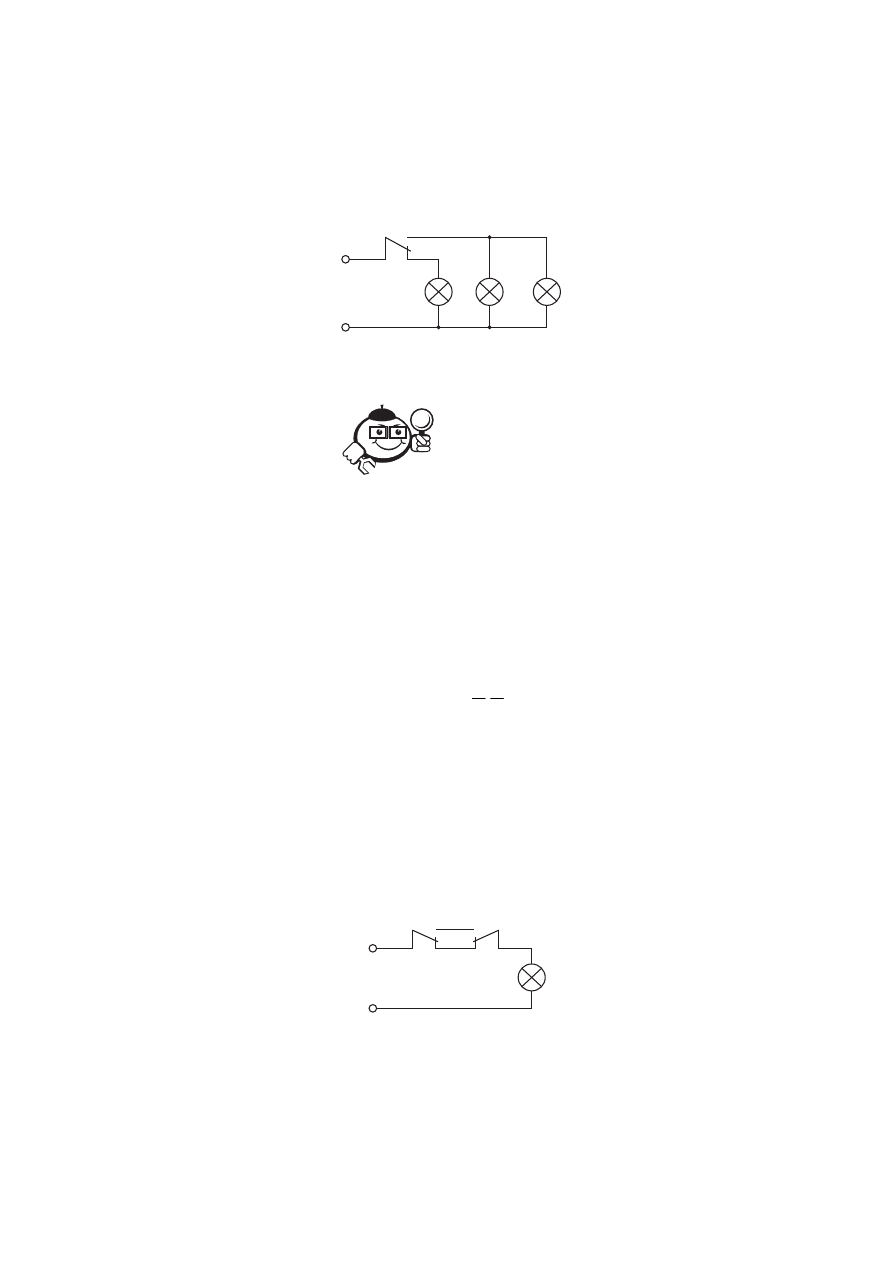
сначала соединим параллельно, а за-
тем подключим к сети через разомкнутый контакт (рис. 7.14).
Рис. 7.14
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.8
· · · · · · · · · · · · · · · · · · · · · · ·
Дано: два тумблера, содержащие по одной переключательной группе кон-
тактов, и осветительная лампа. Лампа горит, если оба тумблера включены или
выключены. Если же включен только один тумблер, то лампа не горит. Постро-
ить контактную структуру, управляющую лампой согласно этим условиям.
Чтобы найти булеву функцию, описывающую работу искомой схемы,
также нет необходимости строить таблицу истинности. Непосредственно из
условия следует, что
,
B
A
B
A
f
+
=
где A и B – тумблеры и они же логические переменные, интерпретируемые, как
показано в предыдущем подразделе; f – функция, соответствующая состоянию
лампы с той же интерпретацией: лампа горит, если цепь замкнута, т. е. f = 1, и
лампа не горит в противоположном случае. Схема, соответствующая этой
функции, приведена на рисунке 7.15.
Рис. 7.15
На практике эта структура известна как схема управления одной лампой с
двух мест [37, с. 260]. Согласно схеме, как она изображена на рисунке 7.15,
лампа горит. Выключить её можно любым тумблером. Например, тумблер A
220 В
A
H
1
H
2
H
3
220 В
A
B
f
155
переведём в верхнее положение. Лампа погаснет. Включить её можно также
любым тумблером, например переводом в верхнее положение тумблера B. Те-
перь в единичном положении находятся оба тумблера. Любым из них лампу
можно выключить и т. д. Общее решение задачи управления лампой с любого
числа мест приведено в [23].
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.9
· · · · · · · · · · · · · · · · · · · · · · ·
Дано: три тумблера A, B и C, содержащие по одному замыкающему кон-
такту, и три лампы накаливания H
1
, H
2
, H
3
. Требуется построить контактную
структуру, работающую следующим образом. Если тумблер A выключен (т. е.
A = 0), то все лампы выключены, причём не горят они независимо от состояний
тумблеров B и C. Если A = 1, то горит лампа H
1
также независимо от состояний
тумблеров B и C, но при B = 0 лампы H
2
и H
3
не горят независимо от состояния
тумблера C. Если же A = B = 1, то горит лампа H
2
независимо от состояния тум-
блера C. При A = B = 1 и C = 0 лампа H
3
не горит. При A = B = C = 1 горят все
три лампы.
Булевы функции, описывающие работу искомой структуры, можно соста-
вить, как и ранее, без таблицы истинности. Однако во избежание каких-либо
ошибок всё же лучше перечисленные условия работы схемы отразить в таблице
(табл. 7.1).
Таблица 7.1
№ A
B C H
1
H
2
H
3
0
1
2
3
4
5
6
7
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
0
0
1
1
1
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
1
Три тумблера – A, B и C – имеют восемь двоичных состояний. Все они
перечислены в левой половине таблицы 7.1. В трёх правых колонках размеще-
ны функции H
1
, H
2
и H
3
, описывающие состояния соответствующих ламп. Так