ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16665
Скачиваний: 202
156
как при A = 0 все лампы не горят, то во всех трёх правых колонках первых че-
тырёх строк ставим нули. При A = 1 горит лампа H
1
. Отмечаем это единицами в
строках 4, 5, 6, 7 колонки H
1
. Согласно условию, при A = 1 и B = 0 лампы H
2
и
H
3
не горят. В связи с этим в строках 4 и 5 колонок H
2
и H
3
записываем нули.
При A = B = 1, C = 0 лампа H
3
не горит. Отмечаем это нулём в строке 6 колонки
H
3
. При A = B = C = 1 горят все лампы, поэтому в последней строке колонки H
3
записываем единицу.
Минимальные ДНФ функций H
1
, H
2
и H
3
имеют вид:
H
1
= A; H
2
= AB; H
3
= ABC.
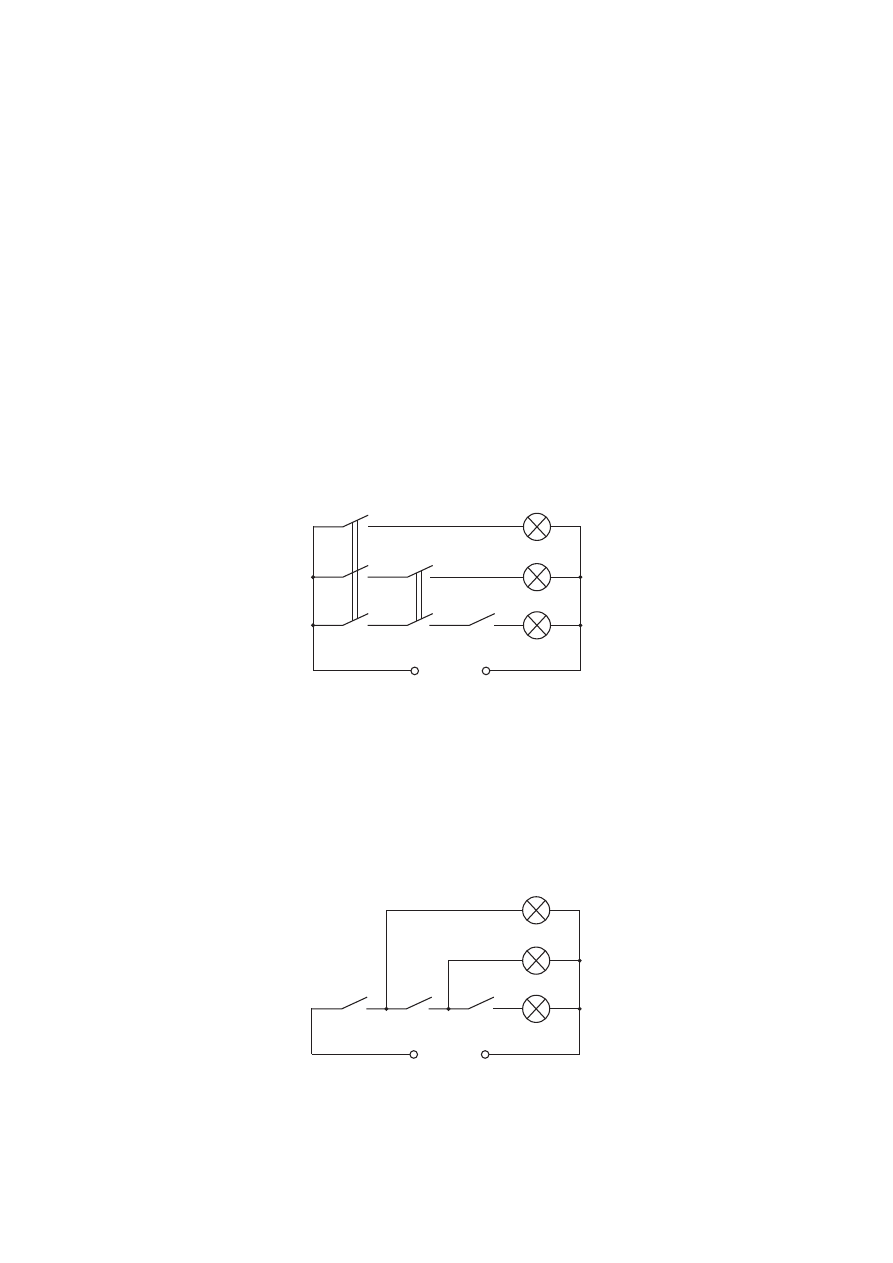
Если схему построить непосредственно по этим функциям, то получится
структура, показанная на рисунке 7.16. Очевидно, что эта схема не удовлетво-
ряет условию задачи по числу контактных групп тумблеров. Поэтому упроще-
ние необходимо продолжить.
Рис. 7.16
В данном случае систему функций представим в виде:
H
1
= A; H
2
= H
1
B; H
3
= H
2
C.
Соответствующая структура приведена на рисунке 7.17, она полностью
удовлетворяет требованиям, сформулированным в условии задачи.
Рис. 7.17
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
220 В
A
H
1
H
2
H
3
B
C
220 В
A
H
1
H
2
H
3
B
C
157
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.10
· · · · · · · · · · · · · · · · · · · · · ·
Дано: две осветительные лампы H
1
и H
2
одинаковой мощности, соеди-
нённые последовательно и подключенные к сети переменного тока напряжени-
ем 220 В, и две кнопки A и B. Когда кнопки не нажаты, лампы горят вполнакала
(т. е. соединены последовательно). При нажатии кнопки A лампа H
1
гаснет, а
лампа H
2
горит в полный накал. Если же нажать кнопку B, то в полный накал
загорается лампа H
1
, а лампа H
2
гаснет. Если кнопки A и B нажать одновремен-
но, то обе лампы горят вполнакала. Требуется построить контактную структу-
ру, работающую в соответствии с этими условиями.
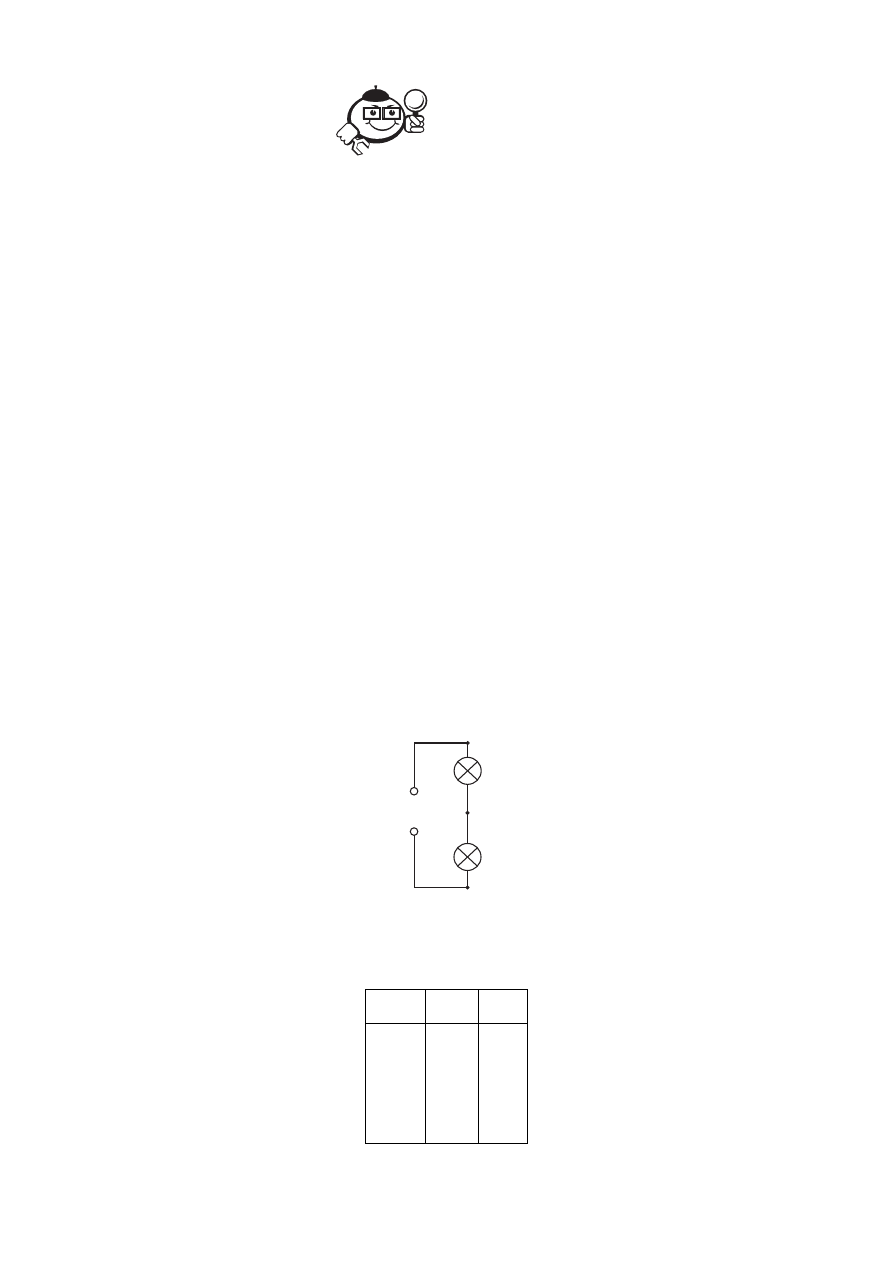
Представим работу схемы в виде таблицы. На рисунке 7.18 лампы соеди-
нены последовательно и включены в сеть 220 В. Если замкнуть точки 1 и 2, то
лампа H
1
погаснет, а лампа H
2
будет гореть в полный накал. Отмечаем это в
таблице 7.2: в колонке 1–2 ставим единицу на пересечении со строкой 10, где
указано: A = 1 (кнопка A нажата) и B = 0 (кнопка B не нажата). Это значит, что
при нажатии кнопки A точки 1 и 2 соединятся между собой. В колонке 2–3 ста-
вим нуль (иначе будет короткое замыкание). Аналогичный случай в строке 01,
где указано, что при нажатии кнопки B соединятся точки 2 и 3. В строках 00 и
11 ставим нули, так как в обоих случаях лампы должны быть соединены после-
довательно.
Рис. 7.18
Таблица 7.2
A B 1–2 2–3
0 0
0 1
1 0
1 1
0
0
1
0
0
1
0
0
220 В
H
1
H
2
1
2
3
158
Булевы функции (табл. 7.2), описывающие работу схемы, имеют вид:
.
;
3
2
2
1
B
A
f
B
A
f
=
=
−
−
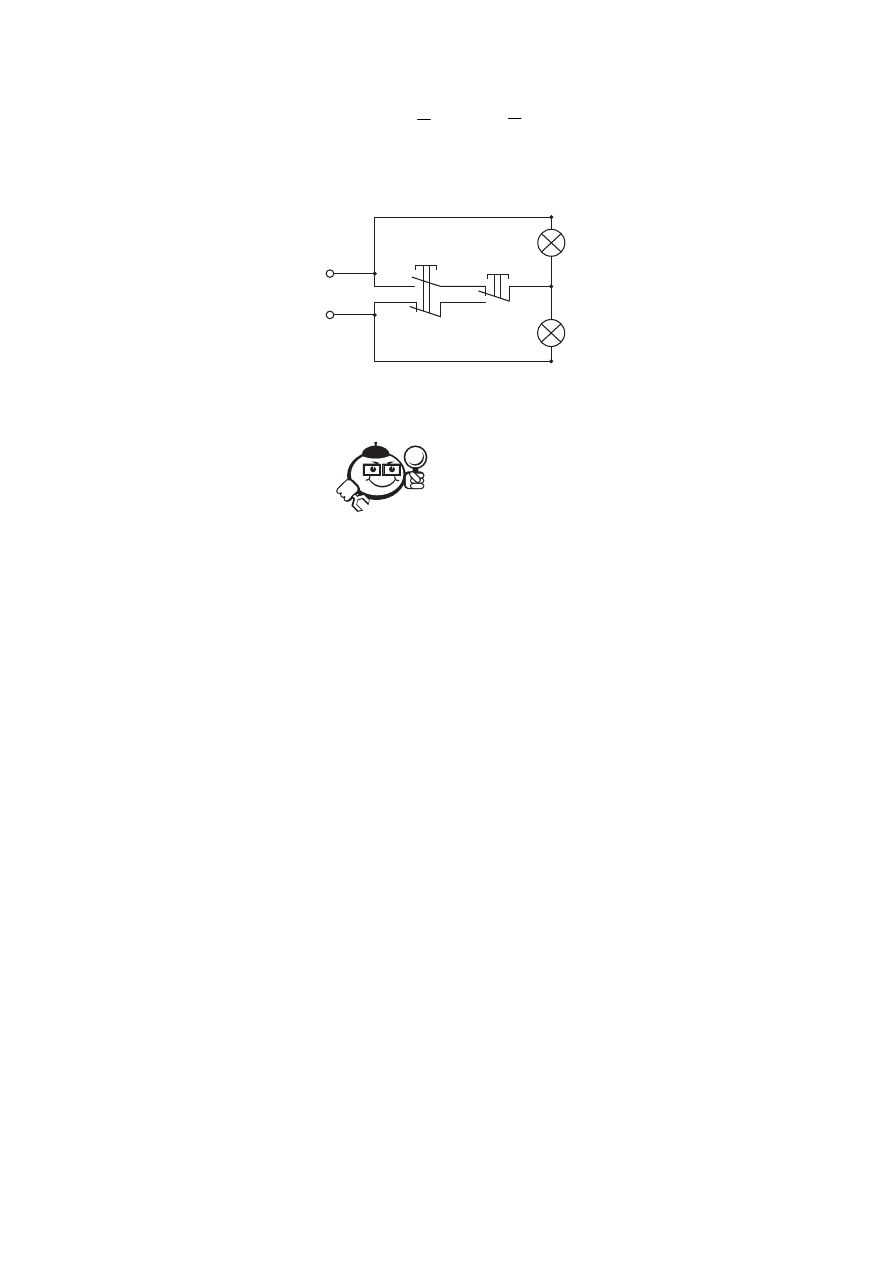
Соответствующая схема приведена на рисунке 7.19.
Рис. 7.19
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 7.11
· · · · · · · · · · · · · · · · · · · · · ·
Четыре осветительные лампы – H
1
, H
2
, H
3
и H
4
– управляются четырьмя
кнопками – A
1
, A
2
, A
3
и A
4
– следующим образом: если ни одна кнопка не нажа-
та, то все лампы погашены. При нажатии i-й кнопки горят первые i ламп (i = 1,
2, 3, 4). Каждая кнопка содержит одну переключательную группу контактов.
Одновременно две и более кнопок не могут быть нажаты.
Поставим в соответствие лампам H
1
, H
2
, H
3
, H
4
функции H
1
, H
2
, H
3
, H
4
, за-
висящие от переменных A
1
, A
2
, A
3
, A
4
. Если A
i
= 1, то горят первые i ламп.
Всего необходимо рассмотреть пять случаев:
0000 – ни одна кнопка не нажата, все лампы не горят;
1000 – нажата кнопка A
1
; горит одна лампа. Допустим, что это лампа H
1
;
0100 – нажата кнопка A
2
; горят две лампы. Пусть это будут H
1
и H
2
;
0010 – нажата кнопка A
3
; горят три лампы, например H
1
, H
2
и H
3
;
0001 – нажата кнопка A
4
; гореть должны все лампы.
Можно составить таблицу истинности, отметив в ней как неопределённые
состояния следующие наборы значений переменных A
1
, A
2
, A
3
и A
4
:
3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15.
В их двоичных кодах содержится две единицы или более. После миними-
зации получим следующий список минимальных ДНФ:
H
1
= A
1
+
A
2
+A
3
+ A
4
;
H
2
= A
2
+ A
3
+ A
4
;
H
3
= A
3
+ A
4
;
220 В
H
1
H
2
1
2
3
A
B
159
H
4
= A
4
.
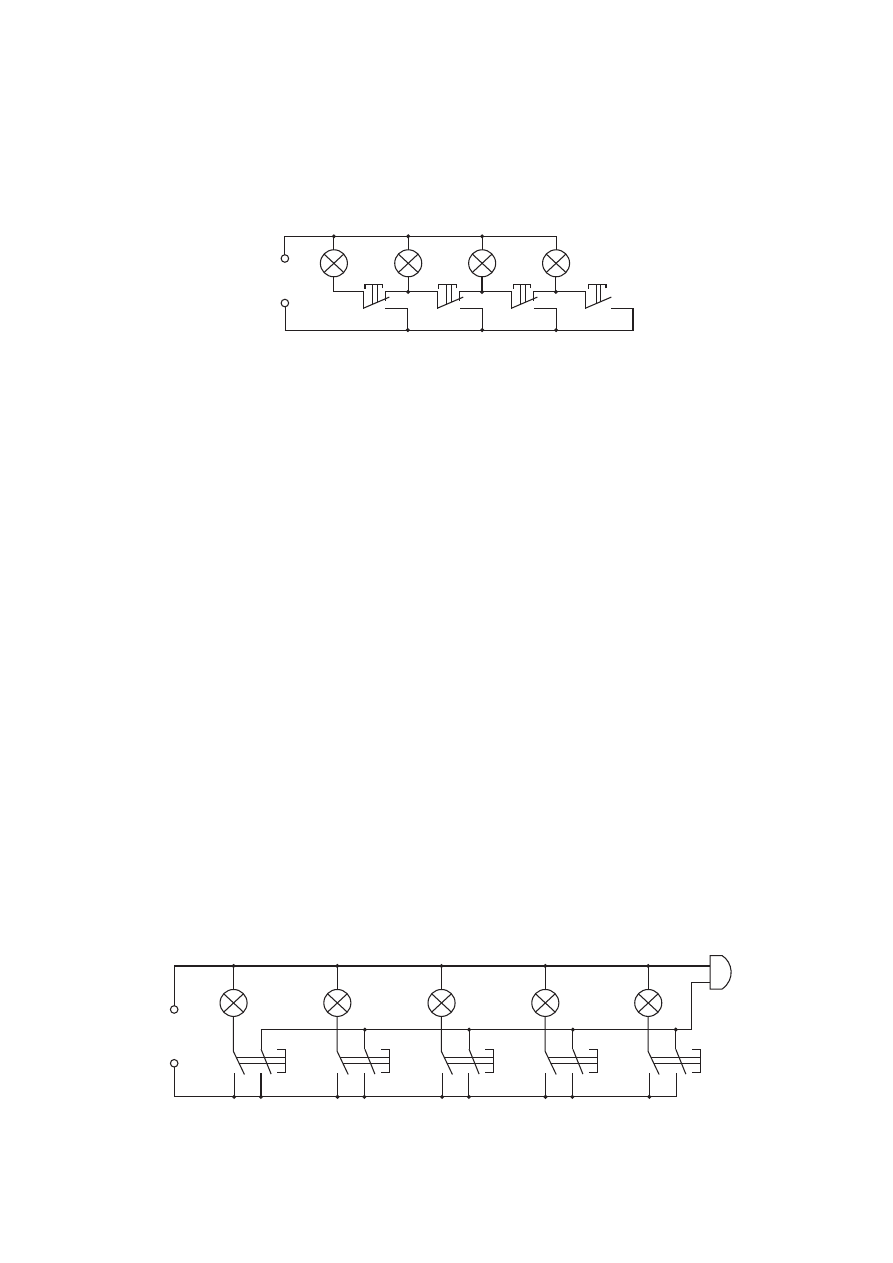
Если на основе этих функций построить контактную структуру, то ока-
жутся невыполненными условия по числу контактов кнопок. Один из вариантов
решения, удовлетворяющий заданным условиям, приведён на рисунке 7.20.
Рис. 7.20
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
7.8 Задача о звонке и осветительных лампах
Схема содержит электрический звонок, n осветительных ламп и n кнопок.
Каждая кнопка содержит один нормально разомкнутый контакт и один нор-
мально замкнутый (i = 1, 2, 3, …, n). Схема работает следующим образом:
1) при нажатии i-й кнопки загорается i-я лампа и одновременно звенит
звонок. При отпускании кнопки лампа гаснет и звонок умолкает;
2) если i-я лампа перегорит, то с нажатием i-й кнопки лишь звенит зво-
нок.
Для определённости примем n = 5. Обычный логический расчёт приводит
к следующей системе булевых функций:
5
4
3
2
1
зв.
A
A
A
A
A
f
+
+
+
+
=
;
;
1
1
A
f =
;
2
2
A
f =
;
3
3
A
f =
;
4
4
A
f =
,
5
5
A
f =
где
зв.
f
– функция, описывающая работу схемы, управляющей звонком;
i
f
–
функция, описывающая работу схемы, управляющей лампой
i
A (i = 1, 2, …, 5).
Схема, построенная на основе этих функций, приведена на рисунке 7.21.
Рис. 7.21
220 В
H
1
H
2
H
3
H
4
A
1
A
2
A
3
A
4
220 В
H
1
A
1
H
2
A
2
H
3
A
3
H
4
A
4
H
5
A
5
Звонок
160
Из схемы видно, что для её реализации необходимы кнопки, содержащие
по два нормально разомкнутых контакта, а согласно условию даны другие
кнопки, содержащие один нормально замкнутый контакт и один нормально
разомкнутый.
Эта задача относится к разряду головоломок, поэтому при её решении от
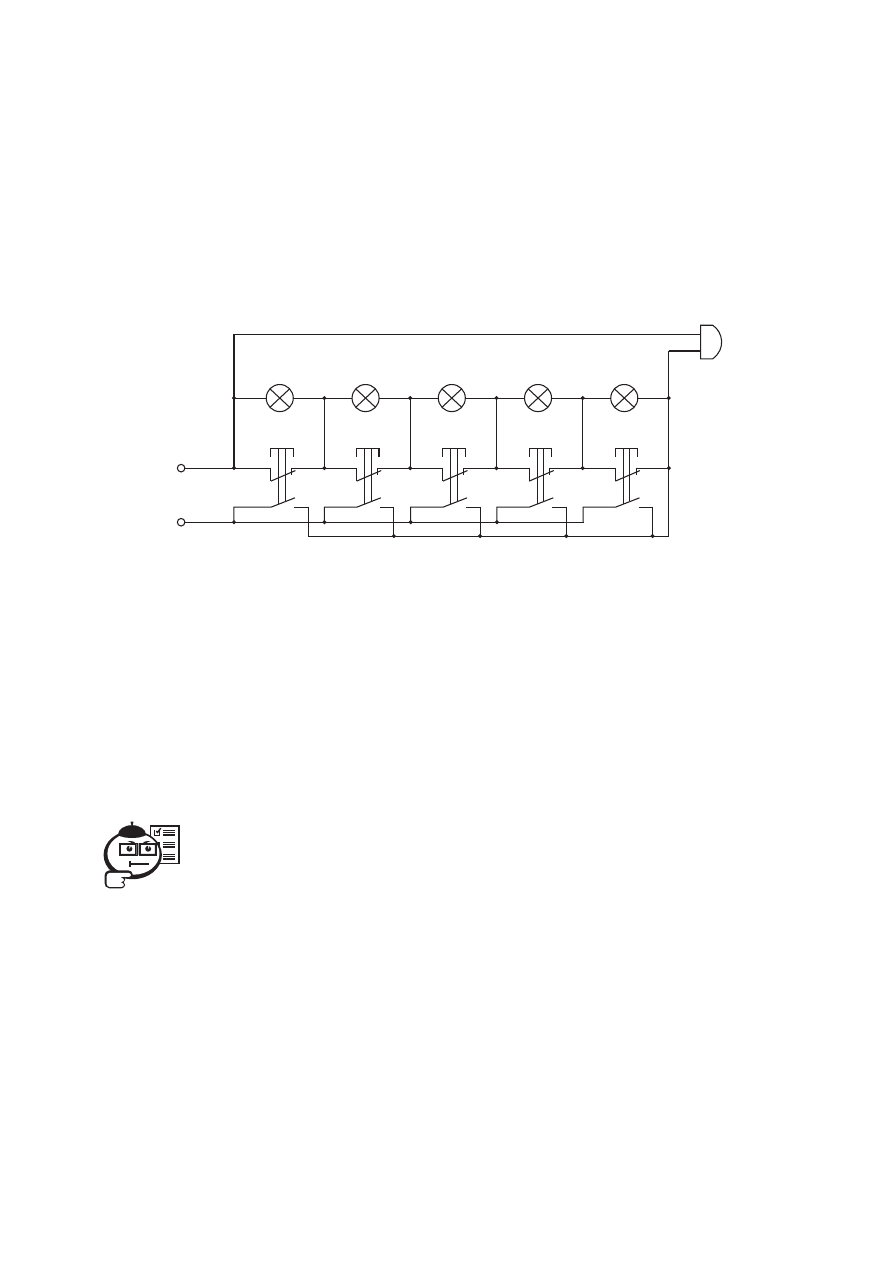
булевой алгебры мало пользы. Решение приведено на рисунке 7.22. Из него
видно, что схема может быть расширена на любое число ламп и кнопок.
Рис. 7.22
Работает схема следующим образом. Пока кнопки не нажаты, звонок не
звенит, и лампы не горят. Нажмём кнопку A
1
. Её первый сверху контакт разо-
мкнётся и лампа H
1
подключится к источнику напряжения 220 В. Вторым кон-
тактом кнопки A
1
замкнётся цепь звонка. Таким образом, с нажатием кнопки A
1
горит лампа H
1
и звенит звонок. Если лампа H
1
окажется перегоревшей, то с
нажатием кнопки A
1
звенит звонок, а лампа H
1
не горит. То же самое относится
и ко всем остальным кнопкам.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. Укажите вопросы, на которые Вы ответите утвердительно.
а. Допустим, что из пяти ламп на рисунке 7.22 лампа H
2
пере-
горела. Будет ли гореть лампа H
1
, если нажать кнопку A
1
?
б. Пусть перегоревшими являются лампы H
1
и H
2
(рис. 7.22).
Будет ли звенеть звонок, если нажать кнопку A
2
?
в. Крайний случай: перегорели все лампы на рисунке 7.22.
Нажали кнопку A
2
. Будет ли звенеть звонок?
г. На рисунке 7.22 лампа H
1
перегорела, остальные исправны.
Нажали одновременно кнопки A
1
и A
2
. Будет ли гореть лампа H
2
?
220 В
H
1
A
1
Звонок
H
2
A
2
H
3
A
3
H
4
A
4
H
5
A
5
a
b
c
d
e
k