ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16661
Скачиваний: 202

161
д. На рисунке 7.22 лампа H
1
перегорела, остальные исправны.
Нажали одновременно кнопки A
1
и A
5
. Будет ли гореть лампа H
5
?
е. На рисунке 7.22 все лампы исправны. Нажали одновремен-
но все кнопки. Верно ли, что гореть будет только одна лампа H
1
?
ж. Лампа H
2
перегорела (рис. 7.22). Будет ли гореть лампа H
1
,
если одновременно нажать кнопки A
1
и A
2
?
2. На рисунке 7.22 все лампы одинаковой мощности. Сколько
вольт покажет вольтметр, если при ненажатых кнопках его подклю-
чить к точкам a и k? b и d?
3. На рисунке 7.22 все лампы одинаковой мощности. Нажали
кнопку A
1
. Сколько вольт покажет вольтметр, если его подключить
к точкам a и b? a и e?
4. На рисунке 7.22 все лампы одинаковой мощности. Одно-
временно нажали кнопки A
1
и A
2
. Сколько вольт покажет вольтметр,
если его подключить к точкам a и b? b и d? c и k? a и e?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
7.9 Инверсные структуры
Суть задач, рассматриваемых в данном параграфе, состоит в следую-
щем. Дана контактная структура, реализующая булеву функцию f. Требуется
построить на её основе инверсную структуру, т. е. реализующую булеву
функцию
.
f
Если заданная схема является параллельно-последовательной, то мож-
но сначала найти соответствующую ей булеву функцию f, затем – её инвер-
сию
,
f представить инверсию f в минимальной ДНФ или КНФ, повысить
порядок (если это возможно) и построить искомую структуру. Очевидно, что
получившаяся схема будет параллельно-последовательной. Если окажется,
что в этой схеме содержится больше контактов по сравнению с исходной, то
следует воспользоваться методом построения двойственных графов, так как
с его применением обеспечивается возможность построения инверсных
структур с тем же числом контактов, что и в исходной структуре.
В случае мостиковых структур также можно строить параллельно-
последовательные схемы, но они обычно сложнее мостиковых, поэтому сле-
дует сразу обратиться к теории графов, если граф схемы является планар-
162
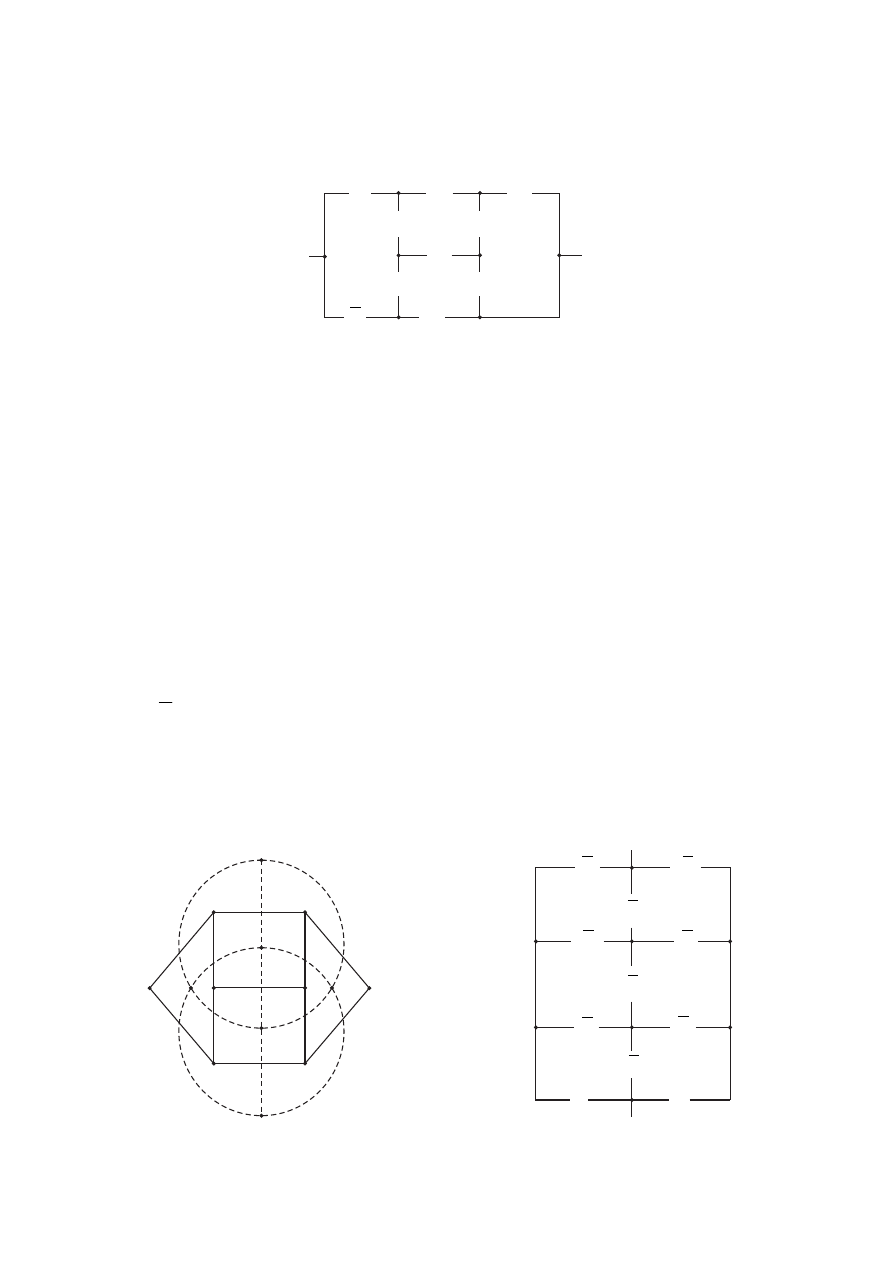
ным. Построение инверсной структуры проиллюстрируем на примере ри-
сунка 7.23.
Рис. 7.23
Пронумеруем точки соединений проводов на рисунке 7.23 и предста-
вим двухполюсник в виде плоского графа (рис. 7.24). Проведем мысленно
осевую линию через вершины 1 и 8 (полюса схемы). Тогда бесконечная
грань разделится на две части. В верхней части бесконечной грани поставим
вершину а, в нижней – вершину m. Внутренним граням поставим в соответ-
ствие вершины b, c, d, e. Соединим вершины a, b, c, d, e,
m так, как это опи-
сано в п. 3.8. Получившийся инверсный граф изображен пунктиром. На его
основе строим искомый двухполюсник. Ребру {1,2} (рис. 7.24) соответствует
контакт А (рис. 7.23). Это ребро пересекает ребро {a,b} двойственного графа
(рис. 7.24). Следовательно, точки a и b инверсной структуры соединяем кон-
тактом A . Аналогичным образом заменяем инверсными контактами все реб-
ра двойственного графа. Получилась инверсная структура (рис. 7.25), содер-
жащая 10 контактов, т. е. столько же, сколько и в случае заданной схемы. Её
полюсами являются выводы a и m.
Рис. 7.24
Рис. 7.25
A
2
D
B
3
F
C
1
8
f
E
A
K
K
4
5
6
7
A
2
3
1
8
m
4
5
6
7
b
c
d
e
a
A
C
A
m
d
c
e
b
a
E
K
D
F
B
A
C
K
163
Способ нахождения инверсных структур с применением теории графов
является высокоэффективным, но применим только к таким контактным
структурам, которым соответствуют планарные графы.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
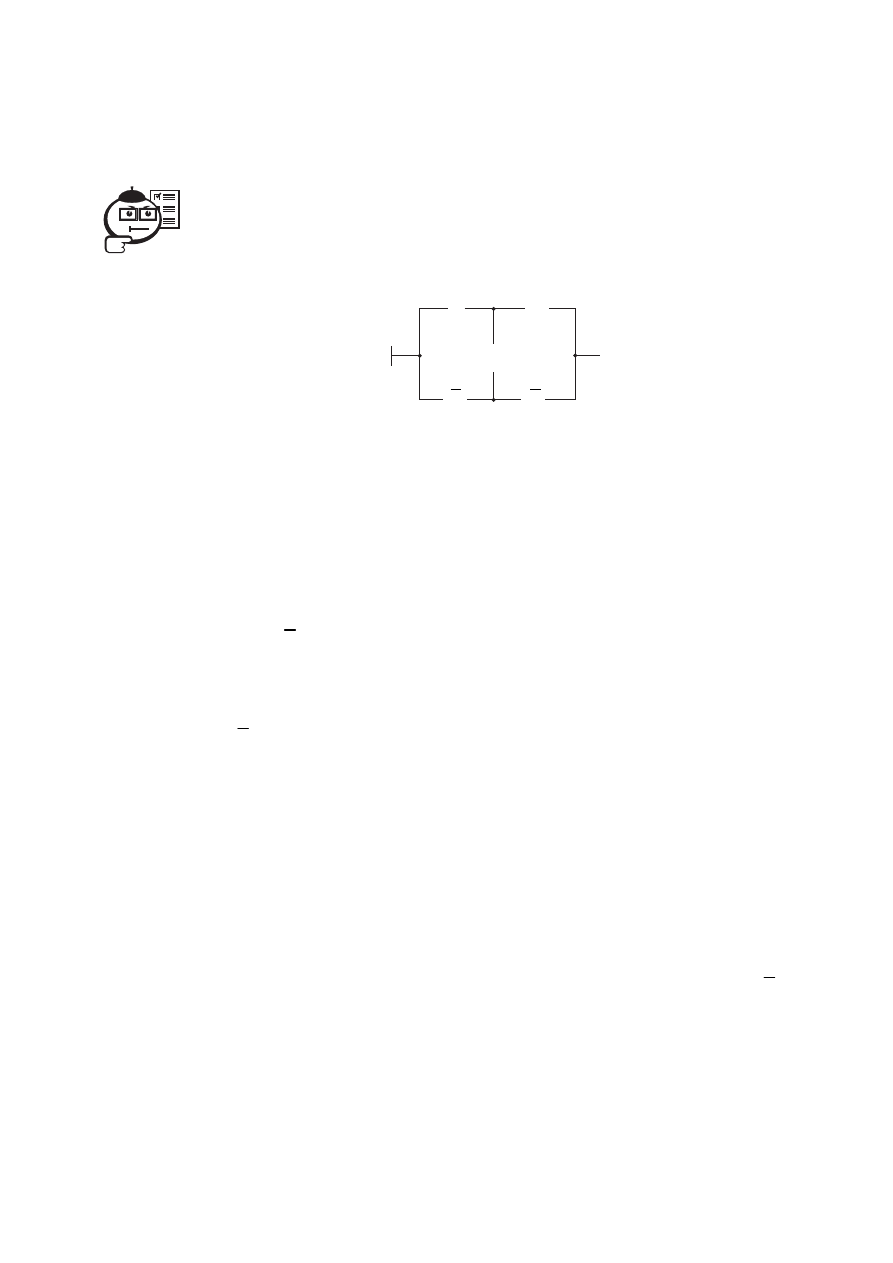
1. На рисунке 7.26 изображена мостиковая структура.
Рис. 7.26
а. Укажите число простых импликант, число вхождений ар-
гументов и число инверсных букв минимальной ДНФ функции f.
б. Перечислите (в порядке возрастания) номера минтермов
функции f.
в. Перечислите (в порядке возрастания) номера минтермов
функции f .
г. Укажите число простых импликант, число вхождений ар-
гументов и число инверсных букв минимальной ДНФ функ-
ции
.
f
2. Постройте инверсную структуру по рисунку 7.27. Найди-
те:
1) число знаков дизъюнкции, число вхождений аргументов
и число инверсных аргументов минимальной ДНФ функции f;
2) число знаков дизъюнкции, число вхождений аргументов
и число инверсных аргументов минимальной КНФ функции f;
3) число знаков дизъюнкции, число вхождений аргументов
и число инверсных аргументов минимальной ДНФ функции
;
f
4) десятичные эквиваленты двоичных наборов значений ар-
гументов, на которых инверсная структура находится в проводящем
состоянии.
A
A
C
D
f
B

164
Рис. 7.27
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
A
A
C
f
B
D
C
A

165
8 Комбинационные схемы
8.1 Электронная интерпретация булевых формул
В комбинационных схемах двоичные переменные и логические операции
интерпретируются иначе по сравнению с контактными элементами:
1) двоичным переменным A
i
(i = 1, 2, 3, …, n, где n – число переменных)
ставятся в соответствие электронные запоминающие элементы – триг-
геры с парафазными выходами: один из выходов прямой (неинверс-
ный) – A
i
, другой инверсный – ;
i
A
2) на входах и выходах логических элементов может быть один из двух
уровней напряжения: низкий (обычно равный нулю) и высокий (не
равный нулю, например, 5 В);
3) единичному значению всех логических переменных соответствует
высокий уровень напряжения, нулевому – напряжение, равное нулю;
4) логической операции конъюнкции соответствует электронный эле-
мент, называемый схемой (элементом) И. Выходное напряжение схе-
мы И равно высокому уровню только в том случае, если высокие
уровни поданы на все его входы. Следовательно, выходное напряже-
ние элемента И равно нулю при подаче низкого уровня хотя бы на
один из его входов;
5) булевой операции дизъюнкции соответствует логический элемент
ИЛИ. Выходное напряжение элемента ИЛИ равно низкому уровню
только в том случае, если низкий уровень подан на все его входы.
Следовательно, чтобы получить высокий уровень на выходе схемы
ИЛИ, достаточно подать высокий уровень хотя бы на один из её вхо-
дов;
6) операции инверсии соответствует одновходовой элемент НЕ (инвер-
тор). Если на его вход подать низкий уровень напряжения, то на вы-
ходе окажется высокий уровень. Если на вход подать высокий уро-
вень, то выходное напряжение будет равным нулю;
7) в соответствии с операцией суперпозиции выходы одних элементов
можно подключать ко входам других элементов.
Согласно данной интерпретации каждой булевой функции, представлен-
ной в форме любого порядка, соответствует вполне определенная комбинаци-
онная схема в виде сети элементов И, ИЛИ, НЕ, и всякой комбинационной схе-