Файл: Верба В.С. - Авиационные комплексы радиолокационного дозора и наведения (Системы мониторинга) - 2008.pdf

Рис. 3.10 

ложной цели, обусловленное превышением порога обнаружения шумами или. 

преднамеренными помехами, при наличии признака маневра цели дополнитель­
но «завязывается» новая траектория. Таким образом, траектория цели на k-м так­

те раздваивается: одна траектория сохраняет характер движения цели, который 

был на более ранних тактах, другая, новая, соответствует маневру цели. На сле­

дующем такте обнаружения (или через один такт) неопределенность, связанная с 

наличием двух траекторий, устраняется путем стирания данных о новой ветви 
траектории, если получила подтверждение траектория для неманеврирующеи 
цели. Если же маневр подтвердился, то стираются данные о продолжении «ста­
рой» траектории. Другое возможное решение состоит в том, что применяется 

фильтр Калмана с новой моделью движения цели, обусловленной маневром. 

3.3. Алгоритмы автоматического сопровождения целей 

в режиме обзора с адаптивной коррекцией прогноза 
и бесстробовой идентификацией радиолокационных 
измерений 

Расширение номенклатуры сверхманевренных самолетов [1-3] и интен­

сивное развитие групповых действий с большим числом самолетов в сложных 
быстроизменяющихся условиях применения, потребовали разработки более со­
вершенных разновидностей АСЦРО, основанных на использовании более 
сложных моделей движения, бесстробовых методов идентификации и более 

сложных алгоритмов адаптивной фильтрации. Некоторые варианты таких ал­
горитмов АСЦРО приведены в [6, 15, 16]. 

Ниже рассматривается один из перспективных алгоритмов АСЦРО, в ко­

тором органично сочетаются высокая точность оценивания координат при со­
провождении маневрирующих целей, основанная на адаптивной коррекции 
прогноза, и высокая разрешающая способность, дающая возможность досто­
верно сопровождать близкорасположенные цели при весьма незначительной 
требуемой производительности бортовой вычислительной системы [13]. 

Для решения этой задачи целесообразно использовать алгоритм адап­

тивной аналого-дискретной фильтрации с коррекцией прогноза, который 
позволяет для процесса 

(3.23) 

по идентифицированным измерениям 

(3.24) 

где 

(3.25) 

сформировать оценки по правилу 

(3.26) 

(3.27) 

(3.28) 

(3.29) 

(3.30) 

(3.31) 

χ, х

э

, χ - n-мерные векторы состояния, экстраполяции и оценок; Φ - пере­

ходная матрица состояния; ζ - m-мерный ( m < η ) вектор измерений; Η - мат­
рица связи ζ и χ; D

x

 и D

H

 - ковариационные матрицы шумов состояния ξ

χ

 и 

измерений ξ

Η

 ; τ - интервал экстраполяции; Τ - период обращений к цели; 

Q - признак наличия измерений; К

ф

 - матрица коэффициентов усиления не-

вязки - апостериорная и априорная ковариацион­

ные матрицы ошибок оценивания; Ε - единичная матрица; 

(3.32) 

(3.33) 

- адаптивная поправка прогноза, оптимальная по минимуму функционала ка­

чества [14] 

(3.34) 

в котором - соответственно матрицы штрафов за точность прибли­

жения χ κ ζ и за величину управляющих поправок u . 

Решение о принадлежности полученного измерения (3.24) той или иной из 

экстраполируемых траекторий (3.27) принимается по минимуму функционала 

(3.35) 

формируемого по результатам полученных измерений на основе вычисления 

Uy для всех j-x экстраполируемых траекторий. Очевидно, что при соответствии 

полученных измерений экстраполируемой траектории они незначительно от­

личаются от в (3.32) и u(k) будет минимальным. Если измерения 

приходят от другой цели, то невязка в (3.32) увеличивается, что приводит к 

увеличению и

у

· и, соответственно, к увеличению функционала (3.35). Та траек­

тория, для которой функционал (3.35) будет наименьшим, и считается иденти­

фицированной. Использование бесстробового метода идентификации, осно­
ванного на экстремальном (3.35), а не на пороговом критерии, позволит суще­
ственно снизить недостатки стробовой идентификации [15]. 

Ниже будут рассмотрены совместно функционирующие алгоритмы экс­

траполяции, идентификации радиолокационных измерений и коррекции 

результатов экстраполяции по идентифицированным измерениям в пред­
положении, что завязка траектории уже выполнена одним из известных спосо­
бов [6]. Этап ранжирования целей и сброса траекторий не рассматривается. 

В существующих бортовых РЛС алгоритмы многоцелевого сопровожде­

ния базируются на использовании простейших моделей движения с постоян­
ными скоростями [8, 11]. Принципиальной причиной использования таких гру­
бых моделей в АК РЛДН являются большие интервалы времени между поступ­
лениями отраженных сигналов при механическом сканировании антенной, 
превышающем время жизни сложных гипотез движения воздушных целей. Ис­
пользование ФАР с электронным управлением лучом позволяет существенно 

сократить интервалы времени между обращениями к одной цели. С учетом это­
го возможно использовать для прогноза модели движения третьего порядка: 

в которых Д и V - дальность до цели и скорость сближения с ней; ε

Γ

, ε

Β

 и 

ω

Γ

, ω

Β

 - соответственно углы визирования и угловые скорости линий визиро­

вания в горизонтальной и вертикальной плоскостях; - продольное 
и поперечные в горизонтальной и вертикальной плоскостях ускорения; к -
номер интервала дискретизации - центрированные гауссов-

ские шумы состояния с известными дисперсиями D^ ,  D

j r

 и Ό-

Β

 . 

Следует отметить, что модели состояния (3.36)-(3.44) обеспечивают оце­

нивание всех фазовых координат, используемых в современных методах наве­
дения. 

Для формирования оценок всех фазовых координат (3.36)-(3.44) в соответ­

ствии с критерием наблюдаемости [10] необходимо, как минимум, измерять 
дальность и углы визирования ε

Γ

 и ε

Β

. При использовании импульсно-

доплеровского режима работы РЛС с высокой частотой повторения достаточно 

просто измеряется скорость сближения (доплеровская частота). Тогда модель 
наблюдений определяется отношениями 

(3.45) 

(3.46) 

(3.47) 

(3.48) 

где - измеренные значения дальности, скорости и углов ви­
зирования цели; - центрированные гауссовские шумы из­

мерений с известными дисперсиями 

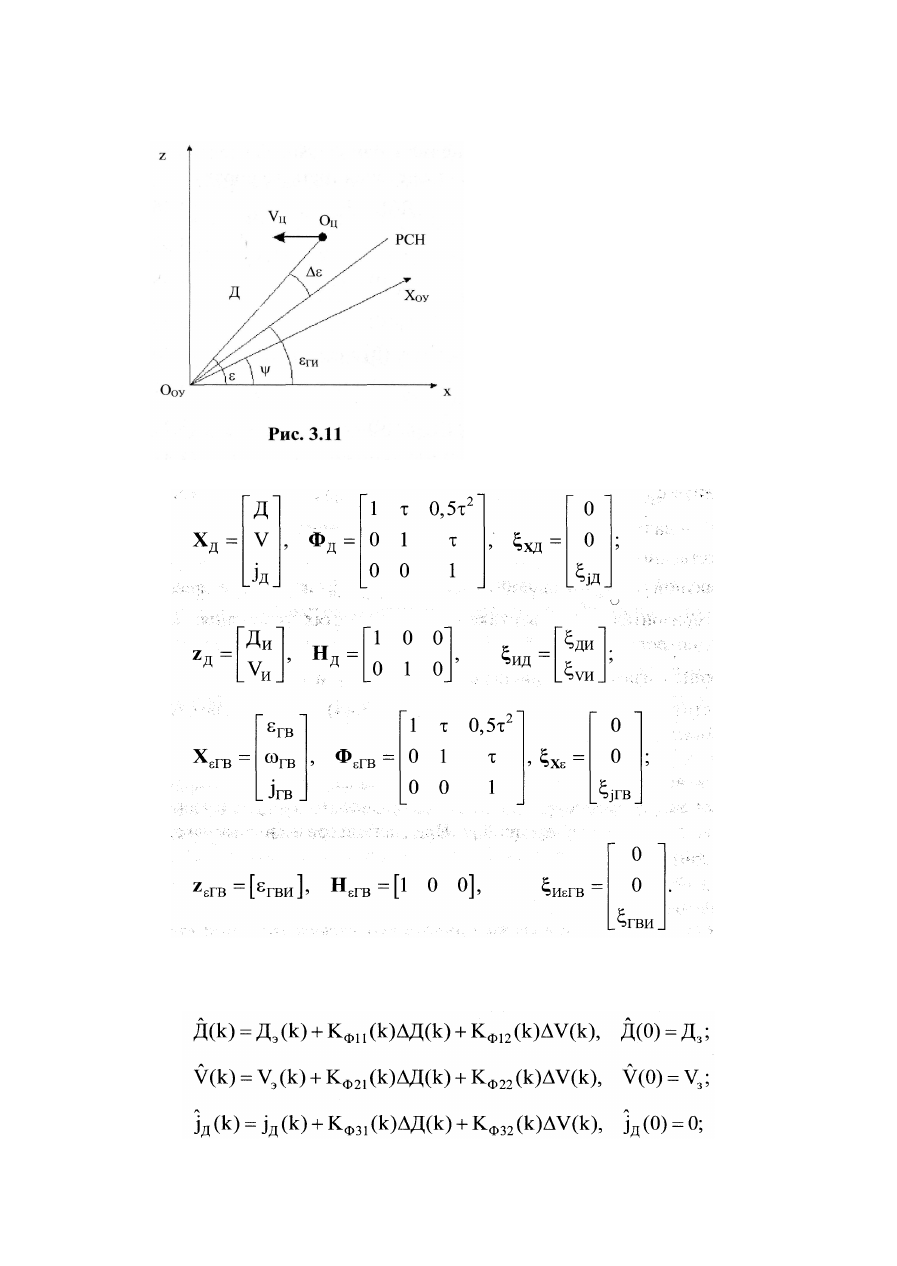
Геометрические соотношения, иллю­

стрирующие взаимное расположение цели 
и носителя РЛС в горизонтальной плоско­
сти, приведены на рис. 3.11. На рисунке 

У

ц

 - вектор скорости цели; 0  Х

о у

- про­

дольная ось носителя РЛС; Δε - текущая 

ошибка измерений; ψ - курс носителя; 
РСН - равносигнальное направление. 

Модели состояния (3.36)-(3.44) и из­

мерителей (3.45)-(3.48) для дальномерного 
и угломерного каналов могут быть пред­
ставлены в векторно-матричной форме 
(3.23) и (3.24): 

(3.49) 

(3.50) 

Используя (3.49) в (3.26)-(3.31), получим алгоритм фильтрации в далъно-

мерном канале РЛС: 

(3.51)