Файл: Верба В.С. - Авиационные комплексы радиолокационного дозора и наведения (Системы мониторинга) - 2008.pdf

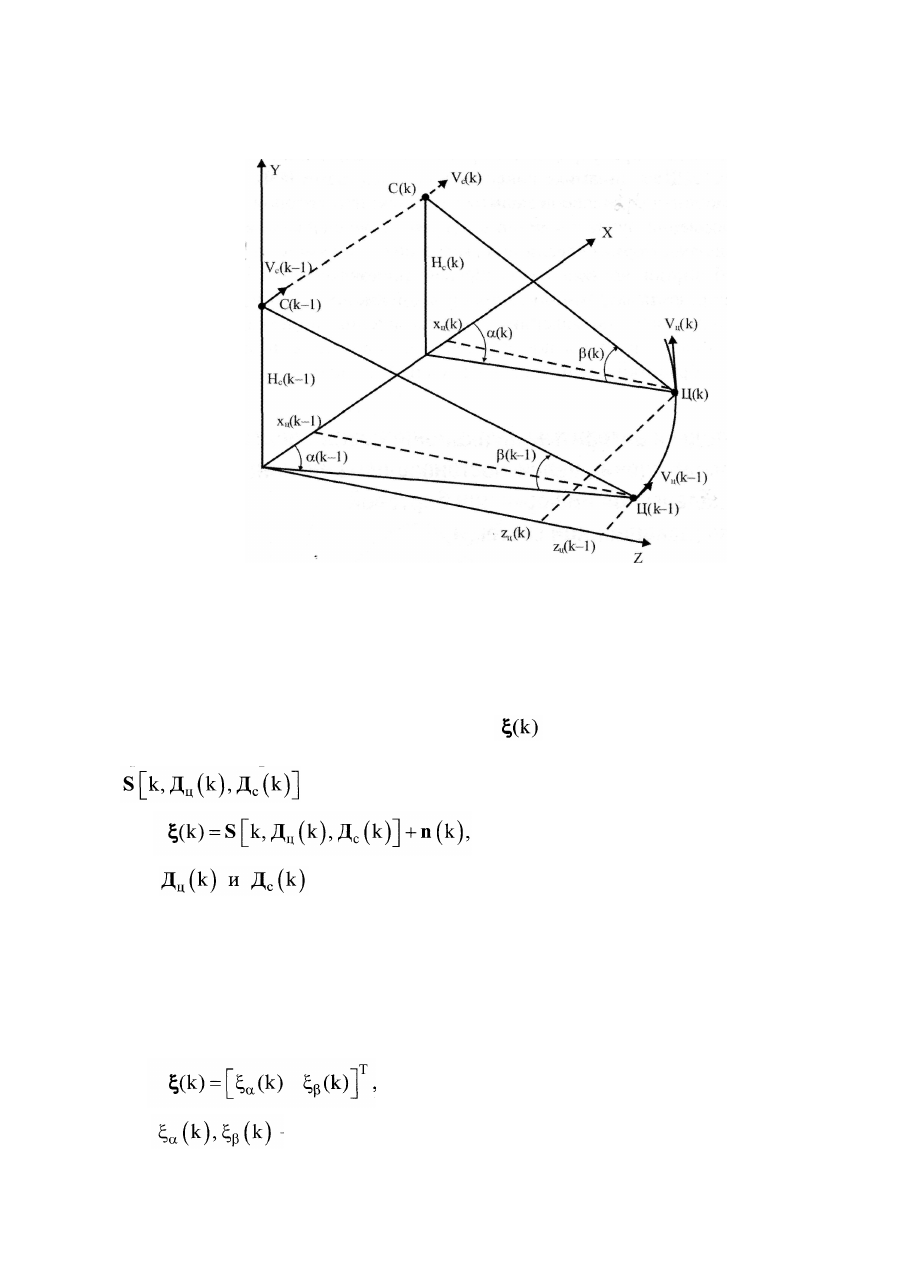
Рис. 4.16 

Пусть самолет-носитель АК РЛДН, представленный на рис. 4.16 точкой 

С, передвигается в неподвижной земной системе координат (НЗСК) OXYZ по 
известной траектории и пусть при этом непосредственному наблюдению дос­
тупен дискретный случайный процесс , значения которого в моменты 

времени к представляют собой аддитивную смесь полезного сигнала 

и дискретного шума n(k): 

(4.2) 

где - векторы состояния движущейся цели и самолета-носи­

теля БРЛС соответственно. 

Состав вектора наблюдения  ξ ^ ) определяется возможностями БРЛС по 

измерению тех или иных пространственных и радиотехнических параметров 
сигналов от подвижных целей. Допустим, что наблюдение пространственных 
параметров сигналов от цели осуществляется по двум углам, поэтому вектор 
наблюдения имеет вид 

(4.3) 

где - измеренные значения азимута и угла места соответственно. 

Глава 4 

Векторную функцию полезного сигнала, зависящую от текущих коорди­

нат самолета и цели, можно представить при помощи нелинейных относитель­
но Д

ц

(к) и Д

с

(к) выражений: 

(4.4) 

Вектор состояния Д

ц

 (к) движущейся цели, от которой зарегистрирован 

ξ ^ ) , в общем случае размерностью п, имеет в составе неизвестные параметры, 

описывающие движение цели. В нашем случае компонентами этого вектора 

являются координаты положения, скорость и ускорение цели по соответст­

вующим координатным осям: 

где - текущие координаты цели в НЗСК, отображаемой точкой Ц 

(рис. 4.16); - скорости и ускорения цели соот­

ветственно по координатам χ и ζ. Положение самолета в системе ΟΧΥΖ оп­

ределяется вектором состояния 

Дискретный шум наблюдения 

(4.5) 

считается стационарным гауссовским белым шумом с нулевым математиче­
ским ожиданием и известной матрицей дисперсий 

(4.6) 

где - дисперсии ошибок измерения углов по каналам азимута и угла 

места. 

Для синтеза алгоритмов оценивания параметров радиоизлучающих объек­

тов помимо рассмотренной модели измерений необходимо располагать апри-

орными данными о возможном поведении объектов, т. е. моделью движения 
цели - ПАП. При выборе модели движения маневрирующего объекта стремят­
ся к тому, чтобы описание этой модели было достаточно простым и в то же 
время правильно отражало реальные траектории. Для различных классов объ­
ектов этому условию отвечают различные модели. Одной из наиболее широко 
используемых на практике является динамическая модель движения [2], со­
гласно которой маневр рассматривается как стационарный случайный марков­
ский процесс с экспоненциальной функцией корреляции ускорения: 

(4.7) 

где <з\ - дисперсия ускорения объекта; - постоянная времени маневра, за­

висящая от его характера. 

В матричной форме разностное уравнение состояния, соответствующее 

модели Зингера для случая ведения наблюдения за движущейся целью в дис­
кретном времени, может быть представлено в виде [15] 

(4.8) 

где Дц(к) - вектор состояния; - фундаментальная матрица решений; 

G(k-l) - переходная матрица возмущений; -

вектор формирующих белых шумов, составленный из независимых случайных 
величин , распределенных по гауссовскому закону с нуле­

вым математическим ожиданием и единичными дисперсиями. 

Применительно к решаемой задаче обработки фундаментальная матрица 

Ф(к, к-1) имеет вид 

/ 

с 

(4.9) 

Выражение для переходной матрицы возмущений G(k -1) приведено в [2], а 

здесь для сокращения записей опущено. 

Полученные уравнения состояния могут непосредственно использоваться 

для построения алгоритма функционирования подсистемы сопровождения це­

лей - постановщиков активных помех. В соответствии с располагаемыми све­

дениями (4.2)-(4.9) имеем задачу нелинейной дискретной фильтрации. Извест­
но, что для получения точных алгоритмов нелинейной фильтрации марковских 
процессов необходимо интегрировать уравнение Стратоновича. В общем слу­
чае эта задача неразрешима. Поэтому обычно рассматривают приближенные 

способы решения. В данном случае используется алгоритм расширенного 
фильтра Калмана, построенный на основе текущей линеаризации нелинейных 
уравнений наблюдения. Эта методика основана на разложении коэффициентов 
уравнения Стратоновича в ряд в окрестности точки оценки фильтруемого па­

раметра при условии, что имеет место малая ошибка фильтрации. 

Разностные уравнения, определяющие значения оценки Д

ц

 вектора со­

стояния и матрицы апостериорных дисперсий D(k) ошибок фильтрации в дис­
кретные моменты времени к, для метода текущей линеаризации имеют вид 

(4.10) 

(4.11) 

где экстраполированные с шага (к-1) на шаг к оценки вектора состояния Д

эц

 и 

матрицы априорных дисперсий D определяются выражениями 

(4.12) 

(4.13) 

Здесь - матрицы дисперсий белых гауссовских дискретных 

шумов состояний и наблюдения, которые будем считать независимыми от номе­
ра шага фильтрации, в силу чего Под 

векторной производной следует понимать матрицу раз­

мерностью m χ η производных полезного сигнала, где m, n - размерности со­

ответственно векторов наблюдения и состояния. 

Для решения разностных уравнений (4.10)-(4.13) необходимо знать на­

чальные условия. При наличии в БРЛС априорной информации о цели, напри­
мер при прицеливании по корабельной РЛС, когда по данным целеуказания от 
других средств известна плотность вероятности вектора состояния цели, в ка­
честве начальной оценки вектора состояния Д

0ц

 и начальной матрицы апосте­

риорной дисперсии D

0

 можно задавать соответственно математическое ожи­

дание и корреляционную матрицу этой плотности вероятности. 

При отсутствии априорных данных о текущих параметрах движения цели 

начальные значения оценок координат х

0ц

, г

0ц

 можно формировать, исходя из 

геометрии прямоугольного треугольника и на основании измерения азимута 

а

0

 и угла места β

0

 цели в соответствии с выражениями: 

где - координаты АК РЛДН в НЗСК в начальный момент времени 

— углы визирования цели по азимуту и углу места. 

Начальные значения скорости и ускорения движения цели выбирают, ис­

ходя из диапазона возможных скоростей и ускорений для заданных типов дви­
жущихся целей. 

Результаты численных расчетов синтезированного квазиоптимального по­

следовательного алгоритма оценивания текущих параметров движения цели по 
критерию минимума среднего квадрата ошибки показали [2,15], что предла­
гаемые алгоритмы работоспособны при наличии флуктуационных погрешно­
стей в измерениях азимута и угла места. Это обстоятельство свидетельствует о 
возможности использования их в БРЛС, в частности при оценке координат ра-
диоизлучающих объектов наземного (надводного) базирования. 

4.4.2. Метод и реализующий его алгоритм самотриангуляции 

в БРЛС для сопровождения целей-ПАП 

В реальных условиях функционирования при полном радиоэлектронном 

подавлении активных радиолокационных каналов информационных средств и 
при отсутствии дополнительных разнесенных источников пеленговой информа­
ции в АКРЛДН определение местоположения излучающих целей (ИЦ) стано­
вится невозможным. В таких ситуациях БРЛС работает автономно и использует 
собственную информацию пассивных радиолокационных каналов для органи­
зации сопровождения данных объектов. Для неподвижных информационных 

средств наземного базирования по собственной пеленговой информации име-