Добавлен: 31.01.2019
Просмотров: 1351
Скачиваний: 4
1. Основная задача физического эксперимента – измерение физических величин для дальнейшего их анализа и установления взаимосвязей между ними – физических законов.
Измерения бывают прямые и косвенные.
В прямых измерениях физическая величина измеряется непосредственно (например, измерение длины предмета линейкой, штангенциркулем или микрометром, силы тока – амперметром и т.д.).
При косвенных измерениях искомая величина не измеряется, а вычисляется по результатам измерений других величин (например, измеряя силу тока и напряжение на зажимах электроплитки, можно вычислить ее тепловую мощность и сопротивление).
В физическом эксперименте любое измерение (прямое или косвенное) дает лишь приблизительное значение данной физической величины. Физика – наука естественная, а абсолютная точность присуща лишь математике.
Действительно, при измерении длины полученный результат будет зависеть, по крайней мере: 1) от точности выбранного нами прибора (штангенциркуль, например, позволяет измерять с точностью до 0,1 мм, а линейка до 1 мм); 2) от внешних условий: температуры, деформации, влажности и т.д.
Пределом измерения прибора называется значение измеряемой величины, при котором стрелка прибора отклоняется до конца шкалы.
Цена деления прибора равна значению измеряемой величины, соответствующему одному делению шкалы прибора.
Класс точности — основная метрологическая характеристика прибора, определяющая допустимые значения основных и дополнительных погрешностей, влияющих на точность измерения.
2. Абсолютная погрешность D - это разность между измеренным X и истинным Xи значениями измеряемой величины. Абсолютная погрешность выражается в единицах измеряемой величины: D = Х - Хи .
Поскольку истинное значение измеряемой величины определить невозможно, вместо него на практике используют действительное значение измеряемой величины Хд. Действительное значение находят экспериментально, путем применения достаточно точных методов и средств измерений. Оно мало отличается от истинного значения и для решения поставленной задачи может использоваться вместо него. При поверке за действительное значение обычно принимают показания образцовых средств измерений. Таким образом, на практике абсолютную погрешность находят по формуле D » Х – Хд . Относительная погрешность d — это отношение абсолютной погрешности измерения к истинному (действительному) значению измеряемой величины (она обычно выражается в процентах)
Способы повышения точности измерений.
· увеличение числа измерений
· изоляция внешних воздействий
· использование более точных приборов
· использование лучших методов измерения
· измерение разными приборами и сверка показаний
Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.
3. По способу измерения погрешность прямых измерений - вычисляются по формуле
![]()
где : t = Sxαs ; Sx — Средняя квадратическая погрешность среднего арифметического, а αs — коэффициент Стьюдента, а А — число, численно равное половине цены деления измерительного прибора.
Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Надежностью результата серии измерений называют вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал. Надежность результата измерения или доверительная вероятность выражается в долях единицы или процентах.
В 1908 году Стьюдент показал, что статистических подход справедлив и при малом числе измерений. Распределение Стьюдента при числе измерений n → ∞ переходит в распределение Гаусса, а при малом числе отличается от него.
Для расчета абсолютной ошибки при малом количестве измерений вводится специальный коэффициент, зависящий от надежности P и числа измерений n, называемый коэффициентом Стьюдента t.
Опуская теоретические обоснования его введения, заметим, что
Δx = S· t. (10)
где Δx – абсолютная ошибка для данной доверительной вероятности;
S – среднеквадратичная ошибка среднего арифметического.
Коэффициенты
Стьюдента
-- это квантили распределения случайной
величины
![]() , где X
распределена по стандартному нормальному
закону, а Y
- по хи-квадрат (независимо от X)
с степенями свободы. В свою очередь,
хи-квадрат -- это закон распределения
суммы квадратов независимых случайных
величин, каждая из которых, в свою
очередь, тоже распределена по стандартному
нормальному закону.
, где X
распределена по стандартному нормальному
закону, а Y
- по хи-квадрат (независимо от X)
с степенями свободы. В свою очередь,
хи-квадрат -- это закон распределения
суммы квадратов независимых случайных
величин, каждая из которых, в свою
очередь, тоже распределена по стандартному
нормальному закону.
При обработке результатов косвенных измерений предлагается следующий порядок операций:
1) Все величины, находимые прямыми измерениями, обработайте в соответствии с правилами обработки результатов прямых измерений. При этом для всех измеряемых величин задайте одно и то же значение надежности P.
2) Оцените точность результата косвенных измерений по формулам (15) – (16), где производные вычислите при средних значениях величин.
3) Если ошибка отдельных измерений входит в результат дифференцирования несколько раз, то надо сгруппировать все члены, содержащие одинаковый дифференциал, и выражения в скобках, стоящие перед дифференциалом взять по модулю; знак d заменить на Δ (или δ).
4) Если случайная и систематическая ошибки по величине близки друг к другу, то сложите их по правилу сложения ошибок. Если одна из ошибок меньше другой в три или более раз, то меньшую отбросьте.
5) Результат измерения запишите в виде:
N = ƒ (¯x, ¯y, ¯z, ...) ± Δƒ.
6) Определите относительную погрешность результата серии косвенных измерений
ε = Δƒ · 100%.
¯¯ƒ¯
4. Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики. Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой.
Мате́рия — фундаментальное физическое понятие, связанное с любыми объектами, существующими в природе, о которых можно судить благодаря ощущениям.
Основные виды материи
-
Адронное вещество — основную массу этого типа вещества составляют элементарные частицы адроны
-
Барионное вещество (барионная материя) — основной (по массе) компонент — барионы
-
Вещество в классическом понимании. Состоит из атомов в обычном смысле этого слова, то есть из атомов, содержащих протоны, нейтроны и электроны. Эта форма материи доминирует в Солнечной системе и в ближайших звёздных системах
-
Антивещество — состоит из антиатомов, содержащих антипротоны, антинейтроны и позитроны
-
Нейтронное вещество — состоит преимущественно из нейтронов и лишено атомного строения. Основной компонент нейтронных звёзд, существенно более плотный, чем обычное вещество, но менее плотный, чем кварк-глюонная плазма
-
Другие виды веществ имеющих атомоподобное строение (например, вещество, образованное мезоатомами с мюонами)
-
Кварк-глюонная плазма — сверхплотная форма вещества, существовавшая на ранней стадии эволюции Вселенной до объединения кварков в классические элементарные частицы (до конфайнмента)
-
Докварковые сверхплотные материальные образования, составляющие которых — струны и другие объекты, c которыми оперируют теории великого объединения (см. теория струн, теория суперструн). Основные формы материи, предположительно существовавшие на ранней стадии эволюции Вселенной. Струноподобные объекты в современной физической теории претендуют на роль наиболее фундаментальных материальных образований, к которым можно свести все элементарные частицы, т.е. в конечном счёте, все известные формы материи. Данный уровень анализа материи, возможно, позволит объяснить с единых позиций свойства различных элементарных частиц. Принадлежность к «веществу» здесь следует понимать условно, поскольку различие между вещественной и полевой формами материи на данном уровне стирается
-
Поле (в классическом смысле)
-
Электромагнитное поле
-
Гравитационное поле
-
Квантовые поля различной природы. Согласно современным представлениям квантовое поле является универсальной формой материи, к которой могут быть сведены как вещества, так и классические поля
-
Материальные объекты неясной физической природы
-
Тёмная материя
-
Тёмная энергия
При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.
Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение.
Линию, по которой движется материальная точка в пространстве, называют траекторией.
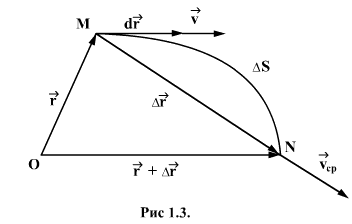
Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ∆r=r-r0, направленный от положения точки в начальный момент времени к ее положению в конечный момент.
Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета. Вектор ускорения характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.
Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета к другой.
5. Перемещение s называют вектор, проведённый из начального положения движущейся точки в её положении в данный момент времени
Путь - длина участка траектории материальной точки, пройденного ею за определенное время.
Скорость - векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.
Ускорение - векторная величина, характеризующая быстроту изменения вектора скорости тела во времени. Ускорение изменяет не только скорость тела, но и направление движения.
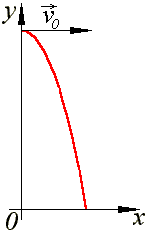
Т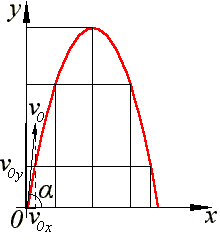 ело
можно бросить и так, чтобы его начальная
скорость v0 будет направлена горизонтально
(α = 0). Так направлена, например, начальная
скорость тела, оторвавшегося от
горизонтально летящего самолета. Легко
понять, по какой траектории будет
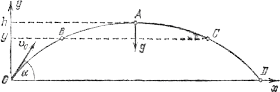
двигаться тело. Обратимся к рисунку 15,
на котором показана параболическая
траектория движения тела, брошенного
под углом α к горизонту. В высшей точке
траектории параболы скорость тела как
раз и направлена горизонтально. Как мы
уже знаем, за этой точкой тело движется
по правой ветви параболы. Очевидно, что
и всякое тело, брошенное горизонтально,
тоже будет двигаться по ветви параболы.
ело
можно бросить и так, чтобы его начальная
скорость v0 будет направлена горизонтально
(α = 0). Так направлена, например, начальная
скорость тела, оторвавшегося от
горизонтально летящего самолета. Легко
понять, по какой траектории будет
двигаться тело. Обратимся к рисунку 15,
на котором показана параболическая
траектория движения тела, брошенного
под углом α к горизонту. В высшей точке
траектории параболы скорость тела как
раз и направлена горизонтально. Как мы
уже знаем, за этой точкой тело движется
по правой ветви параболы. Очевидно, что
и всякое тело, брошенное горизонтально,
тоже будет двигаться по ветви параболы.
 Траекторию
движения тел,
брошенных горизонтально или под углом
к горизонту, можно наглядно изучить в
простом опыте. Сосуд, наполненный водой,
располагают на некоторой высоте над
столом и соединяют резиновой трубкой
с наконечником, снабженным краном.
Выпускаемые струи воды непосредственно
показывают траектории движения частиц
воды. Таким образом можно наблюдать
траектории при разных значениях угла
падения α и скорости v0.
Траекторию
движения тел,
брошенных горизонтально или под углом
к горизонту, можно наглядно изучить в
простом опыте. Сосуд, наполненный водой,
располагают на некоторой высоте над
столом и соединяют резиновой трубкой
с наконечником, снабженным краном.
Выпускаемые струи воды непосредственно
показывают траектории движения частиц
воды. Таким образом можно наблюдать
траектории при разных значениях угла
падения α и скорости v0.
Время движения тела, брошенного горизонтально с некоторой начальной высоты, определяется только тем временем, которое необходимо для свободного падения тела с этой начальной высоты. Поэтому, например, пуля, выпущенная стрелком из ружья в горизонтальном направлении, упадет на землю одновременно с пулей, оброненной случайно в момент выстрела (при условии, что стрелок роняет пулю с той же высоты, на которой она находится в ружье в момент выстрела!..). Но оброненная пуля упадет у ног стрелка, а пуля, вылетевшая из ружейного ствола – во многих сотнях метров от него.
6. Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.
Криволинейное движение более сложный вид движения, чем прямолинейное, поскольку даже если движение происходит на плоскости, то изменяются две координаты, характеризующие положение тела. Скорость и ускорение тела также постоянно изменяются по направлению, а в общем случае и по модулю.
Мгновенная скорость тела при криволинейном движении направлена в любой точке траектории по касательной к траектории в этой точке.
Этот вывод о направлении мгновенной скорости можно подтвердить, наблюдая, как движутся брызги из-под колес буксующего автомобиля или искры при заточке деталей на вращающемся точильном камне.
Рассматривая криволинейное движение тела, мы видим, что его скорость в разные моменты различна. Даже в том случае, когда величина скорости не меняется, все же имеет место изменение направления скорости. В общем случае меняются и величина, и направление скорости.
Таким образом, в криволинейном движении всегда имеется изменение скорости, т. е. это движение происходит с ускорением. Для определения этого ускорения (по величине и направлению) требуется найти изменение скорости как вектора, т. е. требуется найти изменение величины и изменение направления скорости.
При криволинейном движении направление скорости тела меняется, поэтому такое движение является неравномерным, даже если модуль скорости остается постоянным.
Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).
Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
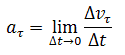
Нормальное
ускорение
- это изменение скорости по направлению
за единицу времени:
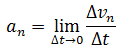
Если начальная скорость брошенного тела направлена вверх под некоторым углом к горизонту, то в начальный момент тело имеет составляющие начальной скорости как в горизонтальном, так и в вертикальном направлениях
7. Рассмотрим подробно движение точки по окружности, при котором v = const. Такое движение называется равномерным движением по окружности. Естественно, вектор скорости не может быть неизменным (v не равно const), так как направление скорости постоянно меняется.
Время, за которое траектория точки опишет окружность, называется периодом обращения точки (Т). Число оборотов точки в одну секунду называется частотой обращения (v). Естественно, перемещение точки за один оборот будет равно нулю. Однако пройденный путь будет равен 2ПиR, а при числе оборотов п путь будет равен 2ПиRn или 2ПиRt/T, где t - время движения.