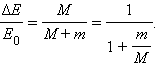Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Потенциальная энергия  — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил.

Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину

Теорема о кинетической энергии - правило для нахождения равнодействующей внешних сил: работа равнодействующей внешних сил, приложенных к телу, равна изменению его полной механической энергии. Изменение кинетической энергии тела равно изменению его потенциальной энергии, взятой со знаком минус, и работе внешних сил.
20. Сила равна градиенту потенциальной энергии, взятого с обратным знаком

Вторая космическая скорость (параболическая скорость, скорость освобождения, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела. Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).

Запишем закон сохранения энергии где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная, v₂ — вторая космическая скорость. Решая это уравнение относительно v₂, получим 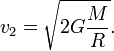. Между первой и второй космическими скоростями существует простое соотношение: Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности планеты):

21. Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.

---

В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

22. Удар — толчок, кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер.

Коэффициент восстановления - в теории удара, величина, зависящая от упругих свойств соударяющихся тел и определяющая, какая доля начальной относительной скорости этих тел восстанавливается к концу удара

,

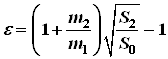
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело. При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках. Пуля массой m, летящая горизонтально со скоростью попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули. Обозначим скорость ящика с застрявшей в нем пулей через Тогда по закону сохранения импульса

При застревании пули в песке произошла потеря механической энергии:

Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:

  Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.

, где v - скорость движения шаров после удара.

Тогда

23. Удар — толчок, кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер.

Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Абсолютно упругий удар может выполняться совершенно точно при столкновениях элементарных частиц низких энергий.

24. Твёрдое тело — это агрегатное состояние вещества, характеризующееся стабильностью формы и характером теплового движения атомов, которые совершают малые колебания около положений равновесия.

Основной закон динамики вращательного движения. Для тела, вращающегося вокруг оси z, , где - момент инерции тела относительно оси вращения z, - угловое ускорение тела, - сумма моментов сил, приложенных к телу, и рассчитанных относительно оси вращения, - индекс суммирования.

---

Момент силы. Вращающее действие силы определяется ее моментом. Моментом силы относительно какой-либо точки называется векторное произведение , где - радиус-вектор, проведенный из точки в точку приложения силы (рис.5). Единица измерения момента силы .

Величина момента силы 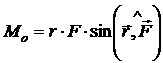, или можно записать , где - плечо силы ( кратчайшее расстояние от точки до линии действия силы).

Моментом инерции тела относительно какой-либо оси z называется сумма произведений масс точек этого тела на квадраты расстояний от этих точек до оси.

, где - масса -той точки , - кратчайшее расстояние от -той точки до оси z.

Для сплошных тел момент инерции определяется через интеграл

, где - расстояние от элемента массы тела до оси z.

25. Сплошной цилиндр или диск радиуса r и массы m Ось цилиндра

Сплошной цилиндр длины l, радиуса r и массы m Ось перпендикулярна к цилиндру и проходит через его центр масс

Прямой тонкий стержень длины l и массы m Ось перпендикулярна к стержню и проходит через его центр масс

Прямой тонкий стержень длины l и массы m Ось перпендикулярна к стержню и проходит через его конец

26. Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Теорема Штейнера: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_C относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

Где J_C — известный момент инерции относительно оси, проходящей через центр масс тела, J — искомый момент инерции относительно параллельной оси, m — масса тела, d — расстояние между указанными осями.

Если алгебраическая сумма моментов всех пар сил, приложенных к телу, имеющему ось вращения, не равна нулю, то тело приобретает угловое ускорение, числовое значение которого прямо пропорционально вращающему моменту М_вр:
М_вр = Jε.

В этом уравнении, выражающем основной закон динамики для вращательного движения тела, множителем пропорциональности является момент инерции тела. Тело с большим моментом инерции труднее привести во вращение.

Единица измерения СИ: кг·м².

Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс

Теорема Штейнера: Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

---

где

J_C — известный момент инерции относительно оси, проходящей через центр масс тела,

J — искомый момент инерции относительно параллельной оси,

m — масса тела,

d — расстояние между указанными осями.

Если   — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии  от неё, равен

,

Основной закон динамики вращения (II закон Ньютона для вращательного движения):
Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на угловое ускорение.

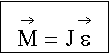
Момент инерции тела характеризует инерционные свойства тела при вращательном движении подобно массе, характеризующей инерционные свойства тела при поступательном движении. Момент инерции тела имеет множество значений, в зависимости от оси вращения.

Если вращающий момент M = const постоянен и момент инерции J = const, то основной закон вращения можно представить в виде

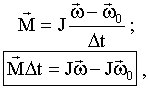
M Δt - импульс момента силы, Jω-момент импульса тела .

27. Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что  , получим
.

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса): 
.

Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:
.

Зако́н сохране́ния моме́нта и́мпульса — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

L=const

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью , то линейная скорость i-ой точки равна  , где , - расстояние от этой точки до оси вращения. Следовательно.

где  - момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости  центра инерции тела, и вращения с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

где  - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

Работа при вращательном движении твердого тела. Рассчитаем работу силы, вызывающей вращательное движение тела вокруг некоторой оси и приложенной к произвольной точке этого тела. Согласно определению работы имеем:

---

A = F·ds = F_·ds. 

Поскольку ds = r·d, то получим следующее выражение для работы:

A = F_·r·d = M·d.

При вращательном движении твердого тела под действием силы Fработа равняется произведению момента этой силы на угол поворота.

Работа переменной силы при повороте тела на конечный угол равняется определенному интегралу от момента сил:

 .

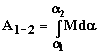Покажем, работа, совершаемая под действием равнодействующего момента сил, равна изменению кинетической энергии тела. Действительно,

A = M·d= I··d = I·(dw/dt)·w·dt = I·d(w²/2),
где M - суммарный момент всех сил, действующих на тело.

Произведя интегрирование по углу, получим:

 A₁₂ = I·w₂²/2 - I·w₁²/2 = E_к.

28(29). Законы Ньютона выполняются только в инерциальных системах отсчета. Системы отсчета, которые движутся относительно инерциальной системы с ускорением, называются неинерциальными. В неинерциальных системах законы Ньютона применять нельзя. Однако законы динамики можно применять и для них, если кроме сил, которые обусловлены воздействием тел друг на друга, ввести в рассмотрение понятие силы особого рода - так называемую силу инерции. 

На тележке к штативу на нити подвешен шарик массой m (рис. 1). Пока тележка покоится или движется прямолинейно и равномерно, нить, которая удерживает шарик, занимает вертикальное положение и сила тяжести Р уравновешивается силой реакции (натяжения) н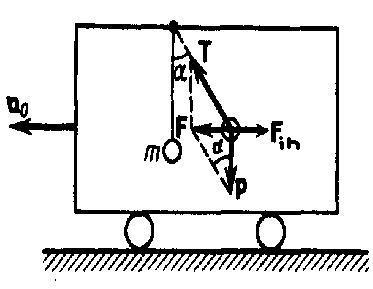 ити Т. 

Рис.1

Если тележку привести в поступательное движение с ускорением а₀, то нить будет отклоняться от вертикали в сторону, обратную движению, до такого угла α, пока результирующая сила F=P+T не даст ускорение шарика, равное а₀. Значит, результирующая сила F направлена в сторону ускорения тележки а₀ и для установившегося движения шарика (теперь шарик движется вместе с тележкой с ускорением а₀) равна F=mg tgα=ma₀, откуда 

 

т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки. 

В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой F_in, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом, 

 (2) 

30. Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета. Пусть диск равномерно вращается с угловой скоростью ω (ω=const) вокруг перпендикулярной ему оси, которая проходит через его центр. На диске установлены маятники, на разных расстояниях от оси вращения и на нитях висят шарики массой m. Когда диск начнет вращаться, шарики отклоняются от вертикали на некоторый угол (рис. 2). 

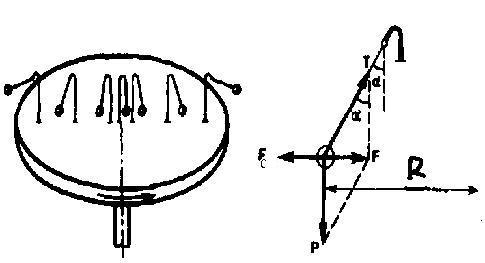
Рис.2

В инерциальной системе отсчета, которая связана, например, с помещением, где установлен диск, происходит равномерное вращение шарика по окружности радиусом R (расстояние от центра вращающегося шарика до оси вращения). Значит, на него действует сила, равная F=mω²R и которая направлена перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести Р и силы реакции (натяжения) нити Т: F=P+T. Когда движение шарика установится, то F=mgtgα=mω²R, откуда 

 

т. е. углы отклонения нитей маятников будут тем больше, чем больше угловая скорость вращения &omega и чем больше расстояние R от центра шарика до оси вращения диска;. 

Относительно системы отсчета, которая связана с вращающимся диском, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой F_с, являющаяся ничем иным, как силой инерции, так как никакие другие силы на шарик не действуют. Сила F_c, называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна 

(3) .
Из формулы (3) следует, что центробежная сила инерции, которая действует на тела во вращающихся системах отсчета и которая направлена в сторону радиуса от оси вращения, зависит от угловой скорости вращения ω системы отсчета и радиуса R, но при этом не зависит от скорости тела относительно вращающихся систем отсчета. Значит, центробежная сила инерции действует во вращающихся системах отсчета на все тела, которые удалены от оси вращения на конечное расстояние, при этом не имеет значения, покоятся ли они в этой системе отсчета (как мы предполагали до сих пор) или движутся относительно нее с некоторой скоростью

---

Смотрите также файлы

• Культурология 911.pdf

• История 910.pdf

• Методичка по английскому.doc

• Лекционная тетрадь ТБУ 2012.docx

• Лекционная тетрадь ФБУ.docx