33. Колебания являются процессами, повторяющимися через одинаковые промежутки времени. В зависимости от физической природы повторяющегося процесса различают колебания механические, электромагнитные, электромеханические и т.п. При механических колебаниях периодически изменяются положения и координаты тел. При электрических – напряжение и сила тока. В зависимости от характера воздействия на колеблющуюся систему различают свободные колебания, вынужденные, автоколебания и параметрические колебания.

Гармоническое колебание описывается периодическим законом

. 

Биение – периодическое изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами.

Результирующее колебание – колебание векторной суммы других колебаний

Сложение гармонических колебаний одного направления и одинаковой частоты. Биения

Пусть совершаются два гармонических колебания одного направления и одинаковой частоты

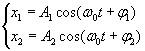 (4.1)

Уравнение результирующего колебания будет иметь вид

Убедимся в этом, сложив уравнения системы (4.1)

Применив теорему косинусов суммы и сделав алгебраические преобразования:

 (4.2)

Можно найти такие величины А и φ0 , чтобы удовлетворялись уравнения

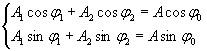(4.3)

Рассматривая (4.3) как два уравнения с двумя неизвестными А и φ0, найдем, возведя их в квадрат и сложив, а затем разделив второе на первое:

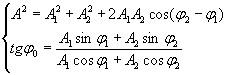
Подставляя (4.3) в (4.2), получим:

Или окончательно, используя теорему косинусов суммы, имеем:

34.

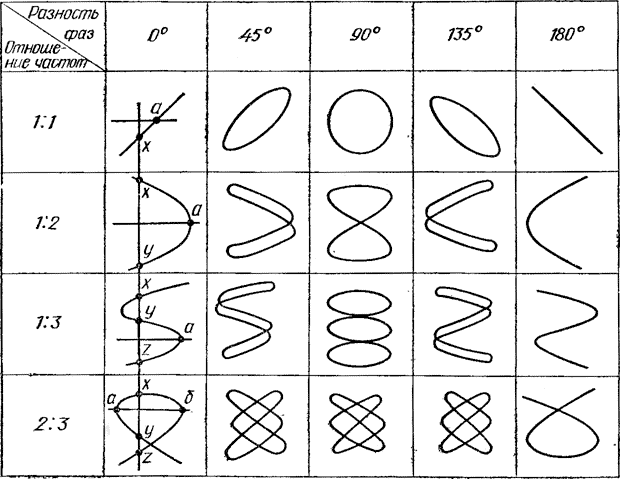
Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде 

 (1) 

где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как 

 

 

и заменяя во втором уравнении  на  и  на  , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей: 

 (2) 

х — смешение — величина, характеризующая положение колеблющейся точки в момент времени t относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в заданный момент времени; 

А — амплитуда колебаний — максимальное смещение тела из положения равновесия;

 Т — период колебаний — время совершения одного полного колебания; т.е. наименьший промежуток времени, по истечении которого повторяются значения физических величин, характеризующих колебание;

  — начальная фаза;  — фаза колебании в момент времени t. Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы (смещение, скорость, ускорение) тела в любой момент времени.

---

-частота-это число колебаний за 1 с, величина обратная периоду.

35. Пружинный маятник – это груз массой М, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под дейтсвием упругой силы F=-kx, где К- жесткость пружины.

Период колебаний – время, за которое тело совершает 1 колебание.

Механическая энергия незатухающих колебаний. Рассмотрим груз на пружине, совершающий гармонические колебания. 

Система, совершающая гармонические колебания называется гармоническим осциллятором. 

Так как F_тр = 0, то система "груз + пружина" является замкнутой и консервативной, то ее полная механическая энергия, равная сумме кинетической и потенциальной энергий, не изменяется:

E = Е_к + Е_п = const.

Подсчитаем полную механическую энергию Е гармонического осциллятора, совершающего колебания по закону x = A·sin(w₀·t +₀). При выводе учтем, что k = w₀²· m.

Е_к = m·²/2 = m·A²·w₀²/2·cos²(w₀·t +₀);
Е_п = k·x²/2 = m·A²·w₀²/2·sin²(w₀·t +₀).

Следовательно,

E = m·A²·w₀².     (9.12)

Энергия гармонического незатухающего осциллятора пропорциональна квадрату амплитуды и собственной частоты и пропорциональна его массе.

36. Период колебаний – время, за которое тело совершает 1 колебание.

Математический маятник – идеализированная система, состоящая из материальной точки массой М, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под дейтсвием сил тяжести.

Важнейший вывод: период колебаний математического маятника не зависит от массы тела!

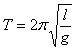
37. Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести.

Период колебаний – время, за которое тело совершает 1 колебание.

Приведённая длина — это условная характеристика физического маятника. Она численно равна длине математического маятника, период которого равен периоду данного физического маятника

где I — момент инерции относительно точки подвеса, m — масса, a — расстояние от точки подвеса до центра масс.

38. Затухающие колебания — колебания, энергия которых уменьшается с течением времени

39. Затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.

Время релаксации τ – время, в течение которого амплитуда А уменьшается в   e    раз.

Логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз. ϴ=1/N, N- число колебаний, совершаемых за время уменьшения амплитуды.

Добротность колебательной системы - отношение энергии, запасённой в колебательной системе, к энергии, теряемой системой за один период колебания. Добротность характеризует качество колебательной системы, т.к. чем больше Д. к. с., тем меньше потери энергии в системе за одно колебание. Q=πN

---

Коэффициент затухания - количественная характеристика сопротивления колеблющейся системы колебательному движению δ=const

40. Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Резона́нс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

41. Закон Архимеда – на тело, погруженное в жидкость/газ, действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости/газа: Fa = pgV, где р- плотность, V- объем

Гидравлический пресс — это промышленная машина, которая позволяет, прилагая в одном месте небольшое усилие, одновременно получать в другом месте высокое усилие. Гидравлический пресс состоит из двух сообщающихся гидравлических цилиндров (с поршнями) разного диаметра. Цилиндр заполняется гидравлической жидкостью водой, маслом или другой подходящей жидкостью

P= pgh – гидростатическое давление

В сообщающихся сосудах жидкость находится на одинаковом уровне всегда. Сообщающиеся сосуды – сосуды соединенные трубкой.

Закон Паскаля - Давление, производимое на покоящуюся жидкость или газ, передается в любую точку жидкости или газа одинаково по всем направлениям.

Гидродина́мика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа

42. Уравнение неразрывной струи – S₂ v₂ = S₁ v₁ = const

Несжимаемая, не обладающая вязкостью жидкость называется идеальной жидкостью 

Это число, которое теперь называют числом Рейнольдса и обозначают Re, характеризует поток и равно:

    Re = vLρ/η

где ρ — плотность жидкости, v — скорость потока, а L — характерная длина элемента потока (в этой формуле важно помнить, что Re — это одно число, а не произведение R × e).

Теперь давайте посмотрим на размерность составляющих числа Рейнольдса:

• размерность коэффициента вязкости η — ньютоны умножить на секунды разделить на кв. метры, или н·с/м². Если вспомнить, что, по определению, н = кг·м/c², мы получимкг/м·с

• размерность плотности ρ — килограммы разделить на кубические метры, или кг/м³

• размерность скорости v — метры разделить на секунды, или м/с

• размерность длины элемента потока L — метры, или м

Для каждого вида течения существует критическое число Рейнольдса, Re_cr, которое, как принято считать, определяет переход от ламинарного течения к турбулентному.

Ламинарное течение – вдоль пока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ним. Турбулентное(вихревое) течение- вдоль потока происходит интенсивное перемешивание и вихреобразование жидкости.

---

Уравнение Бернулли:

Это уравнение и есть уравнение Бернулли. Это уравнение является следствием закона сохранения энергии для установившегося течения идеальной жидкости (p - статическое давление, p*(v*v)/2 - динамическое давление, pgh - гидростатическое давление).

43. Сила сопротивления зависит от формы тела. Придание телу специально рассчитанной обтекаемой формы существенно уменьшает силу сопротивления, так как в этом случае жидкость всюду прилегает к его поверхности и позади него не завихрена.

Если скорость движения тела невелика, то сила сопротивления прямо пропорциональна модулю скорости: F_c = kυ, где k — коэффициент пропорциональности, который зависит от рода вязкой среды, формы и размеров тела. Если скорость движения тела возрастает, то возрастает и сила сопротивления:

Лобовое сопротивление – сила направленная в противоположную сторону движения тела, направлена по потоку

R=C*(pV V)S/2, где V- скорость, р – плотность среды, С – безразмерный коэффициент сопротивления, S –площадь наибольшего поперечного сечения.

Угол атаки – угол к потоку вещества, для крыла чем меньше угол, тем меньше лобовое сопротивление.

Подъемная сила крыла самолета. Воздух, обтекающий крыло, движется над крылом быстрее, чем под крылом. Следовательно, давление под крылом больше, чем над крылом, в результате чего и возникает подъемная сила. 

44. Процесс распространения механических колебаний в среде называют механической волной.

Стоячие волны – волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве. Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн. Волны называют когерентными, если разность их фаз остается постоянной во времени.

Интенсивность волны электромагнитной или звуковой – средняя по времени энергия, которую электромагнитная или звуковая волна переносит в единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны. И. в. пропорциональна квадрату её амплитуды.

Скорость распространения упругих волн – скорость перемещения фазы волны.

Уравнение бегущей волны e(x, t)= Acosω(t+x/v)

45. Звуковыми волнами называются распространяющиеся в среде упругие волны, обладающие частотами в пределах 16-20к гц и слышимые для человека. Инфразвуковые(v<16)и Ультразвуковые(v>20к) человеком не воспринимаются.

Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Его легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, он услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.

---

Интенсивность звука(сила звука) – величина, определяемая средней по времени энергией, переносимой звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны. I = W/(S*t). Для каждой частоты существует наибольшая(порог болевого ощущения) и наименьшая(порог слышимости) интенсивность звука, которые способны вызывать звуковое восприятие.

Громкость звука – субъективная хар-ка звука, зависящая от частоты и амплитуды колебания. Измеряется в децибелах

Высота звука – определяется частотой звуковой волны(периодом волны). Чем выше частота, тем выше звучание.

Тембр звука – звуковое ощущение, определяемое характером акустического спектра и распределения энергии между определенными частотами.

Ревербация звука – процесс постепенного затухания звука в закрытых помещениях после выключения источника звука.

Природа звука(источник звука) – может быть любое колеблющееся в упругой среде со звуковой частотой тело.

---

Смотрите также файлы

• Культурология 911.pdf

• История 910.pdf

• Методичка по английскому.doc

• Лекционная тетрадь ТБУ 2012.docx

• Лекционная тетрадь ФБУ.docx