Файл: Методические указания по выполнению лабораторных работ Дисциплина pg 3307 Прикладная геодезия.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 129
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример расчета
Исходные данные:
Дирекционные углы и длины сторон
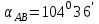
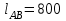 м
м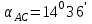
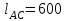 м
мКоординаты пунктов геодезической основы и точки А строительной сетки
| | х | у |
| Шахта | 12601,12 | 5092,17 |
| Карьер | 12244,91 | 6475,02 |
| Пойма | 13400,20 | 6702,09 |
| Точка А | 12217,00 | 5349,00 |
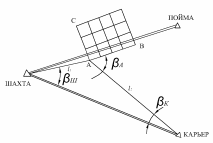
Рисунок 3 –Схема строительной сетки
Порядок выполнения работы:
1.Вычисляем координаты В и С углов строительной сетки
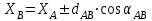
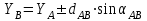
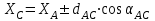
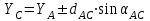
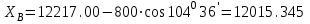
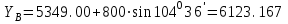
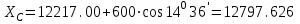
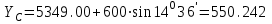
2. Вычисляем дирекционные углы на определенную точку:
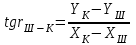
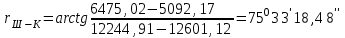 (II четверть)
(II четверть)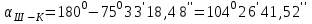
По знакам приращения координат определяем номер четверти в которой находится данная сторона.
3.Находим значение обратного угла
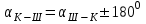
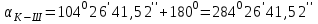
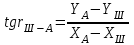
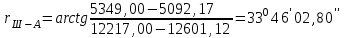 ( II четверть)
( II четверть)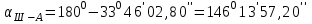
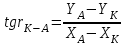
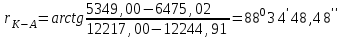 (III четверть)
(III четверть)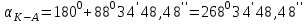
4. Вычисляем разбивочные углы для перенесения точки А в натуру. Разбивочные углы всегда находят по разности дирекционных углов
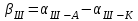
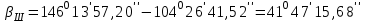
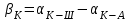
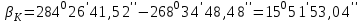
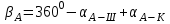
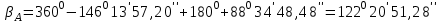
Контроль:
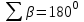
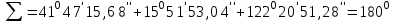
5. Вычисляем горизонтальные расстояния до точки А
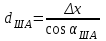 ,
, 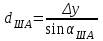 ,
, 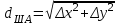
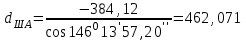 м ,
м , 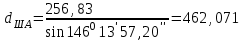 м ,
м , 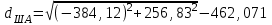 м.
м.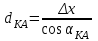 ,
, 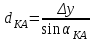 ,
, 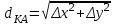
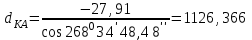 м,
м, 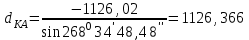 м,
м, 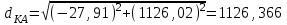
6. При расчете длин сторон на знаки внимания не обращаем. Значение отчета на горизонтальном круге для вынесения в натуру точку А
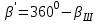
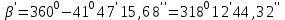
7. Вычисляем разбивочные углы для перенесения точки В и С
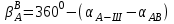
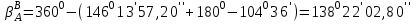
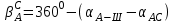
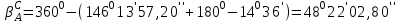
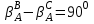
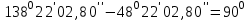
Определяем элементы редуцирования.
1.Вычисляем
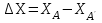 ,
, 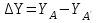
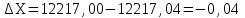 ,
, 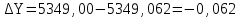
2. Вычисляем
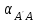
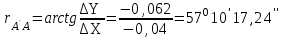
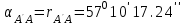
3.Вычисляем длину перемещения
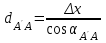 ,
, 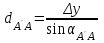 ,
, 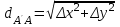
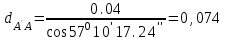 м,
м, 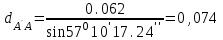 м,
м, 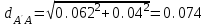 м.
м.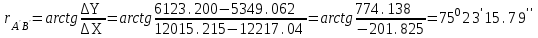 (II четверть).
(II четверть).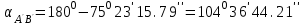
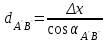 ,
, 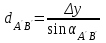 ,
, 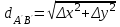
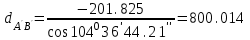 м,
м, 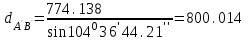 м,
м,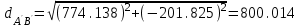 м
м4. Вычисляем горизонтальный угол
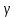 для перемещения точки
для перемещения точки 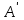
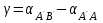
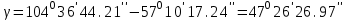
Таблица 5 – Исходные данные для разбивки строительной сетки
| Варианты | Дирекционные углы | Координаты точки А | № варианта | Дирекционные углы | Координаты точки А | ||||
 |  | Х | У |  |  | Х | У | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 127°34’ | 37°34’ | 12 316,00 | 5 419,00 | 16 | 149°58’ | 59°58’ | 12 218,00 | 5 417,00 |
| 2 | 132°15’ | 42°15’ | 12 736,00 | 5 813,00 | 17 | 204°27’ | 114°27’ | 12 305,00 | 5 217,00 |
| 3 | 106°17’ | 16°17’ | 12 315,00 | 5 429,00 | 18 | 107°14’ | 17°14’ | 12 308,00 | 5 215,00 |
| 4 | 104°36’ | 14°36’ | 12 217,00 | 5 349,00 | 19 | 149°27’ | 59°27’ | 12 516,00 | 5 273,00 |
| 5 | 287°19’ | 197°19’ | 12 412,00 | 5 609,00 | 20 | 156°29’ | 66°29’ | 12 317,00 | 5 216,00 |
| 6 | 127°34’ | 37°34' | 12 317,00 | 5 436,00 | 21 | 154°22' | 64°22' | 12 526,00 | 5 493,00 |
| 7 | 234°35' | 153°35' | 12 805,00 | 5 716,00 | 22 | 208°26' | 118°26' | 12 527,00 | 5 117,00 |
| 8 | 174°35' | 84°35' | 12 409,00 | 5 215,00 | 23 | 149°27' | 59°27' | 12 326,00 | 5 108,00 |
| 9 | 15°33' | 285°33' | 12 826,00 | 5 539,00 | 24 | 135°15' | 45°15' | 12 319,00 | 5 415,00 |
| 10 | 102°48' | 12°48' | 12 327,00 | 5 456,00 | 25 | 25°43' | 295°43' | 12 548,00 | 5 489,00 |
| 11 | 149°26' | 59°26' | 12 317,00 | 5 627,00 | 26 | 214°26' | 124°26' | 12 617,00 | 5 709,00 |
| 12 | 204°26' | 114°26' | 12 217,00 | 5 309,00 | 27 | 147°34' | 57°34' | 12 117,00 | 5 236,00 |
| 13 | 114°27' | 24°27' | 12 317,00 | 5 656,00 | 28 | 112°15' | 22°15' | 12 336,00 | 5 413,00 |
| 14 | 158°32' | 68°32' | 12 526,00 | 5 429,00 | 29 | 15°45' | 285°45' | 12 416,00 | 5 129,00 |
| 15 | 149°26' | 59°26' | 12 527,00 | 5 611,00 | 30 | 102°18' | 12°18' | 12 356,00 | 5 497,00 |
Лабораторная работа № 3. Перенесение на местность проектных точек по заданным координатам
Содержанием разбивочных работ является построение в ходе строительства по мере надобности разбивочных элементов с целью указания на местности и на сооруженных частях строящегося объекта осей, размеров и отметок, обеспечивающих необходимую точность исполнения проекта. Необходимая точность разбивочных работ определяется особенностями возводимого сооружения и регламентируется соответствующими строительными нормами и правилами и проектом.
Способ полярных координат. Проектную точку Р (рисунок 4, а) выносят в натуру путем построения на опорном пункте А проектного угла β от направления на другой опорный пункт В и отложения проектного расстояния d. Исходными данными при этом служат координаты точки Р, заданные в проекте, координаты пункта А и дирекционный угол αAB, известные из результатов обработки опорной геодезической сети.
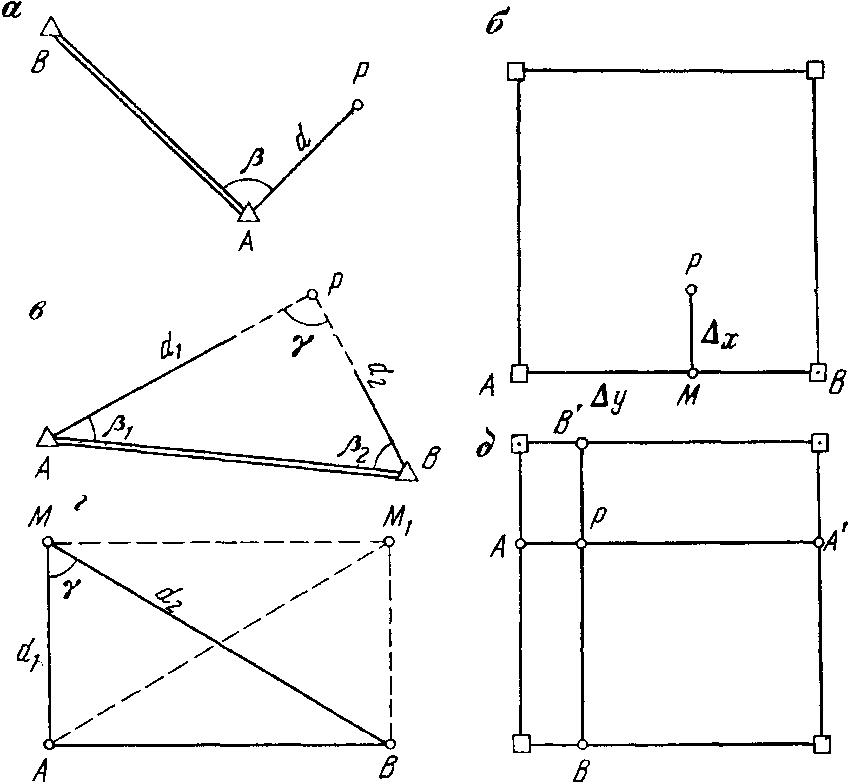
Рисунок 4 — Схемы способов выноса точки в натуру:
а − полярных координат; б − прямоугольных координат; в − прямой угловой засечки; г − линейной засечки; д − створной засечки
Способ применяют, когда благоприятны условия для отложения расстояний мерным прибором, или для разбивки сооружения используется электронный тахеометр, в котором измерение и отложение расстояний автоматизировано.
Точность вынесения точки в натуру оценивают средней квадратической погрешностью:
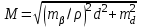 ,
,где mβ − средняя квадратическая погрешность построения угла β в секундах; ρ= 206265»− число секунд в радиане; md − погрешность отложения расстояния d.
Способ прямоугольных координат (рисунок 4, б). Применяется при наличии закрепленной на местности строительной сетки, красной линии застройки или осей строящегося сооружения. С генплана или рабочих чертежей снимают графически или вычисляют по координатам пункта А геодезической основы приращения координат выносимой в натуру точки Р по формуле:
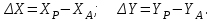
Затем откладывают большее из этих приращений (рисунок 4,
б ) отрезок ΔY) по направлению соответствующей координатной оси. В полученной точке М устанавливают теодолит и, отложив прямой угол, строят перпендикуляр, по которому откладывают меньшее приращение (отрезок ΔX).
Средняя квадратическая погрешность выноса точки данным способом оценивается по формуле:
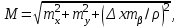
где mх, mу — средние квадратические погрешности отложения соответствующих приращений координат; mβ — погрешность построения прямого угла.
Если разбивка выполняется отложением сначала отрезка Δx, а затем перпендикуляра Δy, то средняя квадратическая погрешность выноса точки оценивается по формуле:
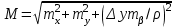 .
.Лабораторная работа № 4. Расчет разбивки закругления в главных точках
План работы:
1. Изучить порядок работ при разбивке закруглений;
2. Выполнить расчеты:
- главных элементов кривой;
- детальной разбивки кривой;
- данных для выноса пикетов на кривую.
Исходные данные для расчетов (угол поворота j, положение точки угла поворота трассы УП и радиус кривой R) задаются преподавателем. Каждому студенту выдается индивидуальное задание.
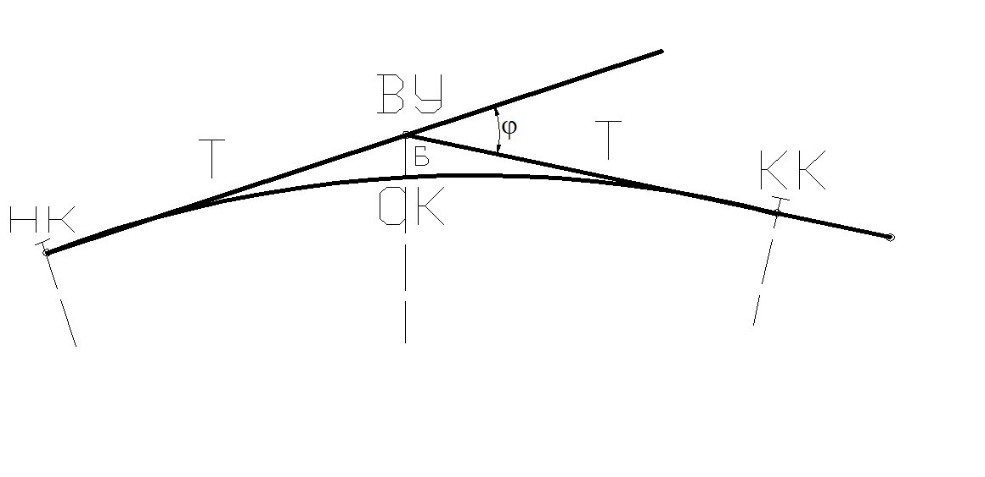
1 Разбивка кривой в главных точках
Главными точками закругления является начало НК, середина СК и конец КК кривой, а элементами – тангенсы Т, кривая К, биссектриса Б, домер Д (рисунок 5).