Файл: Методические указания по выполнению лабораторных работ Дисциплина pg 3307 Прикладная геодезия.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 126
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рисунок 5 - Разбивка кривой в главных точках
Элементы кривой находят по измеренному углу поворота j и радиусу кривой R, заданному согласно техническим нормативам.
1. Тангенс Т – расстояние от точки поворота до начала или конца кривой
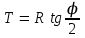 .
.2. Кривая К – длина дуги от начала до конца кривой
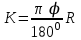 .
.3. Биссектриса Б – расстояние от точки поворота до середины кривой по биссектрисе угла (180 0 - j)
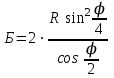 .
.4. Домер Д – разность двух тангенсов и длины кривой
Д=2T-K.
Пример 1. Дано: R=160 м, j=700.
Определить: Т, К, Б, Д.
Решение:
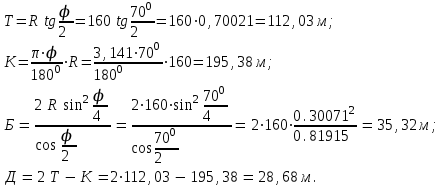
5. Вычисление пикетажного обозначения НК и КК ведется с учетом положения точки УП в следующей последовательности:
УП…………….ПК 9+90,00 Контроль УП……………ПК 9+90,00
- +
Т………………... I+12,03T...………………I+12,03
НК…………….ПК 8+77,97 ПК11+02,03
+ -
К…………………I+95,38 Д……..…………….28,68
КК……………ПК10+73,35 КК……….…..ПК10+73,35
Второй столбец по вычислению пикетажного обозначения конца кривой выполняется для контроля.
Для обозначения на местности точек НК и КК от вершины угла УП в обе стороны по трассе откладывают длину тангенса Т и забивают колышки. Затем при помощи теодолита отмечают направление биссектрисы и, откладывая по ней Б, забивают колышек, получая точку СК. Если величина Б не более 10 м, то направление биссектрисы можно получить откладыванием от точки УП по тангенсам равных отрезков длиной по несколько метров. Середина рулетки, соединяющая концы отрезков, покажет направление биссектрисы.
Далее производится вынос пикетов на кривую и её детальная разбивка.
2 Вынос пикетов на кривую
Вынос пикетов на кривую производится в процессе разбивки пикетажа методом прямоугольных координат. Координаты пикетов находятся по формулам:
Xi=R·sinei; Yi=2R· sin2(εi/2),
где R - радиус кривой;
ei - центральный угол, стягивающий дугу Li, равную расстоянию
от НК или КК до пикета на кривой, вычисляемый из выраже-
ния
ei = 1800 Li /pR .
Пример 2.
Пусть исходными данными для выноса пикетов на кривую являются результаты по разбивке кривой в главных точках (рисунок 6). Требуется вынести на кривую ПК 9 и ПК 10.

Решение:
1. Находим длину дуг L9 и L10 для соответствующих пикетов 9 и 10 из выражений:
L9 = ПК9 – НК = ПК9 – (ПК8+77,97) = 22,03м;
L10 = КК – ПК10 = (ПК10+73,35) – ПК10 = 73,35м.
2. Вычисляем центральные углы e9, e10 по формулам:
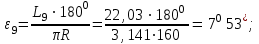
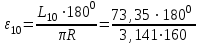 180°=26,3°= 26°18¢.
180°=26,3°= 26°18¢.
3. Определяем координаты ПК9 в системе координат с началом в точке НК
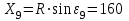 ×0,13716=21,95м;
×0,13716=21,95м;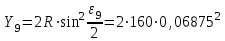 =1,51м .
=1,51м . 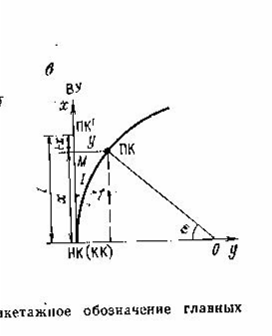
Рисунок 6 - Вынос пикетов на кривую
4.Определяем координаты ПК10 в системе координат с началом в точке КК
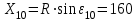 × 0,44307 = 71,09м;
× 0,44307 = 71,09м;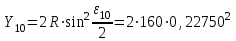 = 16,56м
= 16,56м По вычисленным координатам пикеты наносятся на план кривой в выбранном масштабе. На местности вынос пикетов на кривую производится откладыванием рулеткой или мерной лентой от начала или конца кривой по направлению касательных абсциссXi , построением при помощи эккера перпендикуляров и откладыванием по ним ординат Yi .
Лабораторная работа № 5. Расчет элементов детальной разбивки кривых
Детальная разбивка кривых может выполняться несколькими способами. Наибольшее применение имеют способы прямоугольных координат, продолженных хорд и полярный.
Для каждого способа строится схема, на которой показываются все исходные и вычисляемые элементы. Исходными данными для расчета являются радиус кривой
R и длина дуги или хорды между соседними колышками детальной разбивки, выбираемая согласно таблицы 6.
Таблица 6
| Радиус кривой R, м | Длина дуги 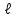 , м , м |
| 10- 35 40- 80 100-190 200-800 свыше 900 | 1 2 5 10 20 |
3.1 Разбивка кривой способом прямоугольных координат
Наиболее точным и простым при детальной разбивке кривых является способ прямоугольных координат, широко применяемый на открытой ровной местности. При этом способе положение каждой точки на кривой определяется прямоугольными координатами Xi и Yi . За начало координат берутся точки НК или КК, за ось абсцисс X- направления касательных (линий тангенсов ), за ось ординат Y – радиусы кривой в точках НК или КК (рисунок 7 ). Координаты точек 1,2,3, …, n вычисляют по формулам :
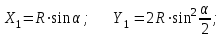
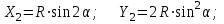
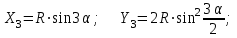
…………………………………….
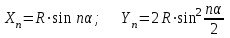 ,
,где a - центральный угол, стягивающий дугу
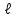 и вычисляемый из выражения
и вычисляемый из выражения 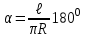 .
.Пример 3
Дано: R=160 м,
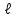 =5 м.
=5 м.Определить: Xi, Yi.
Решение:

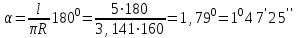 ;
;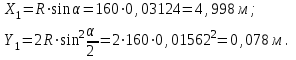
Все данные вычислений координат точек до середины кривой сведены в таблице 7.
Таблица 7
| № точек | Xi, м | Yi, м |
| 1 2 3 …………… 19 | 4,998 9,990 14,930 … 94,050 | 0,078 0,310 0,700 … 30,550 |
Вынесение точек кривой
1,2,3,…….., 19 на местности сводится к откладыванию рулеткой от начала и конца кривой отрезков, равных X1, X2, X3,…, X19, построению при помощи эккера перпендикуляров концов отрезков и откладыванию по ним отрезков, равных Y1,Y2,…,Y19.
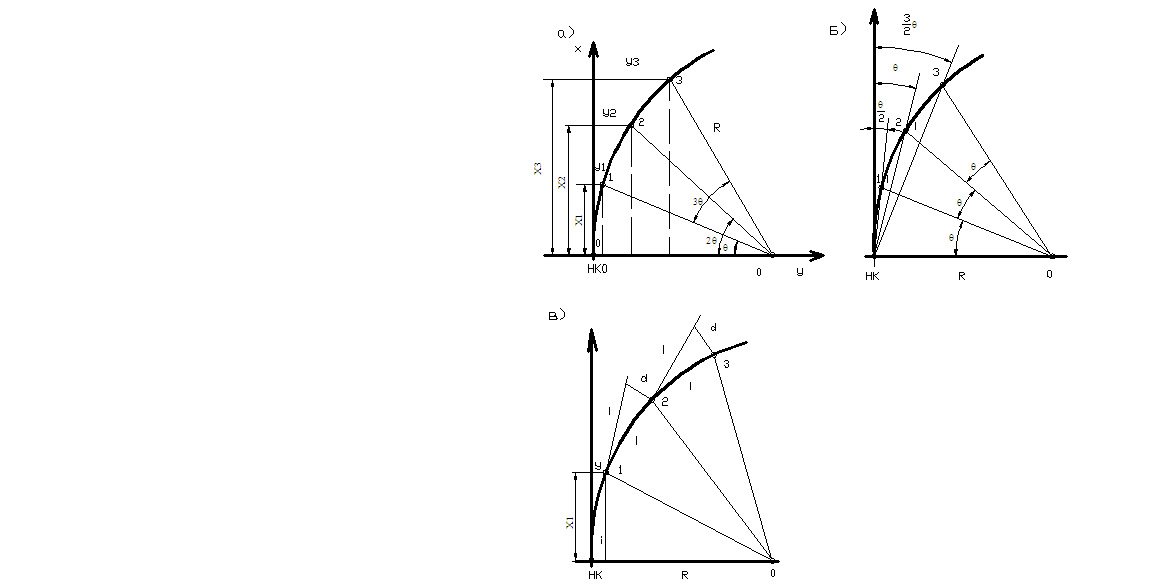
Рисунок 7 - Детальная разбивка кривой: а- способом прямоугольных координат; б-полярным способом; в- продолженных хорд
3.2 Разбивка кривой способом продолженных хорд
Способ продолженных хорд применяют на застроенных участках, в лесных районах и неприступных местах. Детальная разбивка кривой способом продолжения хорд показана на рисунке 7, в.
При этом способе положение первой точки детальной разбивки на кривой получают по координатам X1, Y1, вычисляемым по известным уже формулам
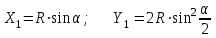 ,
, где угол a находится из выражения
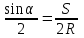 .
.При этом способе положение первой точки детальной разбивки на кривой получают по координатам X1, Y1, вычисляемым по известным уже формулам
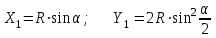 ,
,где угол a находится из выражения
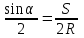
Здесь S – длина хорды между соседними точками детальной разбивки. Для нахождения второй точки продолжают хорду (НК-1) и на этом луче от точки 1 откладывают отрезок, равный S, получая точку 2'.
Положение точки 2 на кривой в натуре находят линейной засечкой отрезкамиs из точки 1 и d из точки 2'. Длина отрезка d вычисляется по формуле:
d = s2/R .
Положение всех остальных точек до середины кривой находят аналогично.
Пример 4
Дано: R=160 м, s= 5 м.
Определить: X1, Y1, d.
Решение:
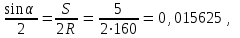 откуда
откуда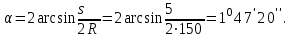
Тогда
