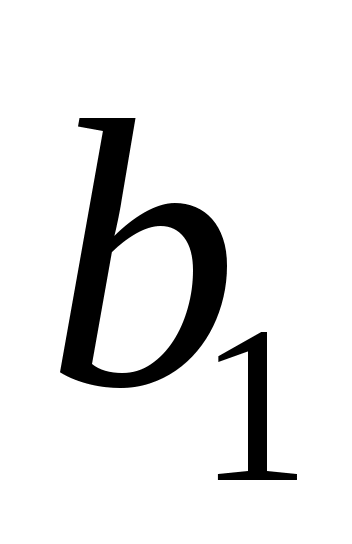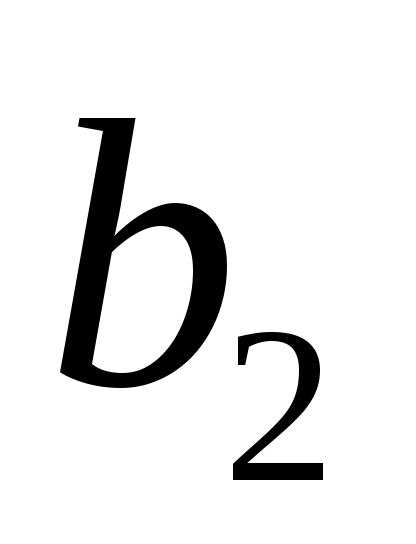, , , , , , , , , , . Тогда мы получим 10! перестановок. Но из этих 10! перестановок такие перестановки как
, , , , , , , , , , ;


, , , , , ,

---

, , , , ;


, , , , , , , , , , ;


…
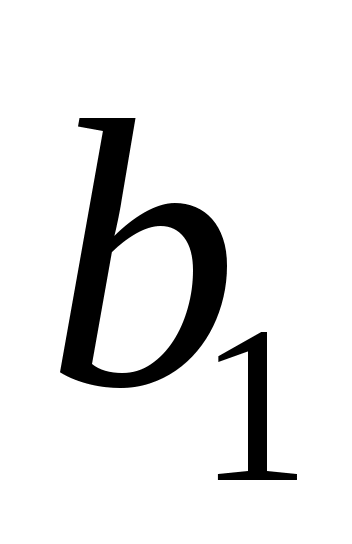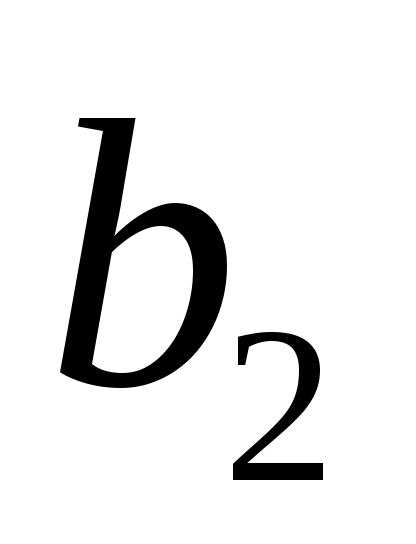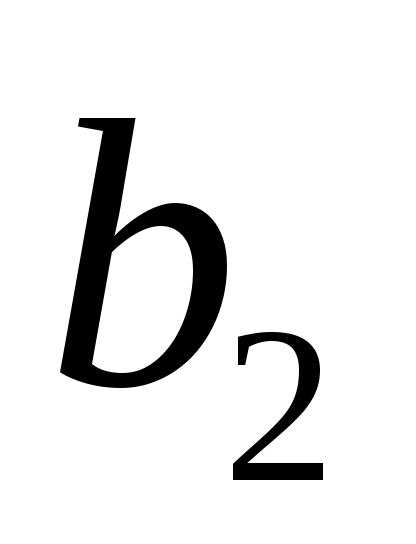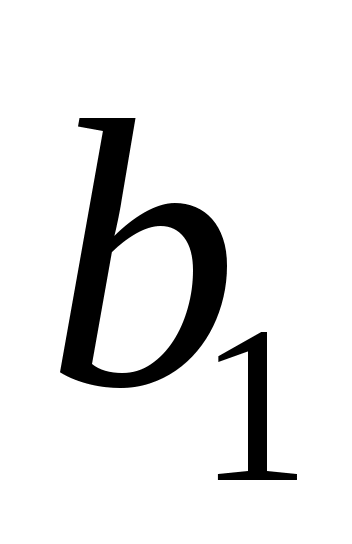при отбрасывании индексов будут одинаковыми. Одинаковыми будут 3! перестановок из a, 2! перестановок из b, 1! перестановок из c, 4! перестановок из d. Общее количество одинаковых перестановок:
Исключим их из общего количества перестановок:

.

В общем случае число перестановок любого мультимножества (множества с повторениями элементов) или перестановок с повторениями равно полиномиальному коэффициенту:



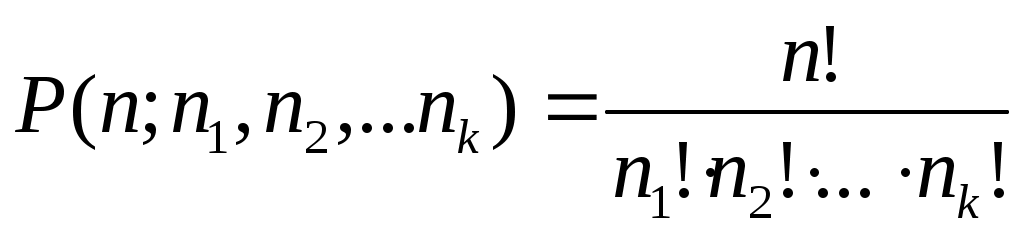
Перестановки с повторениями имеют тесную связь с сочетаниями. Определим их количество: из всех n элементов перестановки место занимают элементы первого типа. Выбор мест для них можно сделать из способами. Из оставшихся

---

мест элементы второго типа занимают место, которое можно выбрать способами…

Согласно правилу прямого произведения число перестановок с повторениями равно:




Задача №1:

Решить пример с использованием формулы через сочетания.



Задача №2:

Сколько существует различных перестановок из букв слова «уссури»?

---

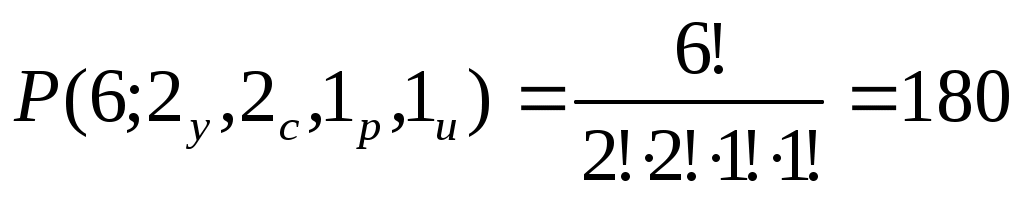
Глава 2. ТЕОРИЯ ГРАФОВ
Рассмотрим конечное множество и множество всех его 2-х элементных множеств. Для произвольных подмножеств называем термином граф всякую пару .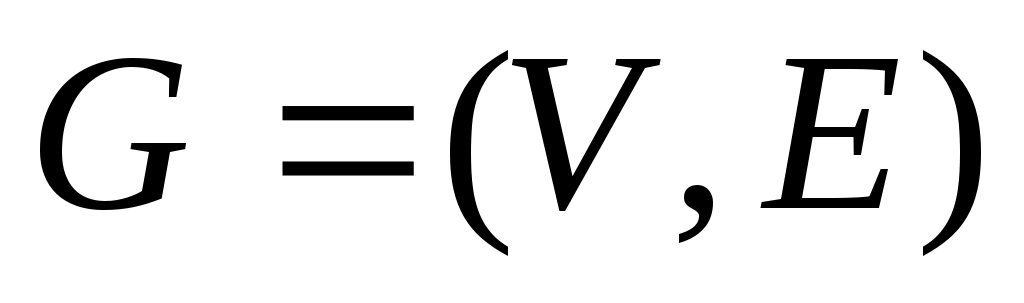

Элементы множества называются вершинами, элементы множества ребрами.

Вершины и ребра графа называются его элементами. Число вершин графа 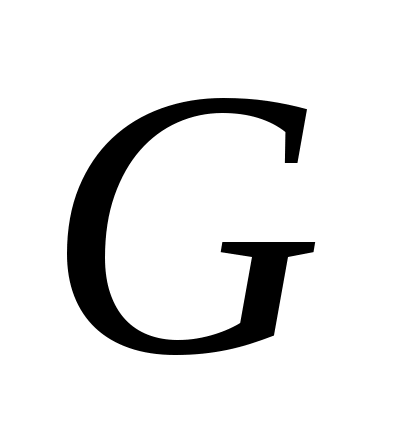называется его порядком и обозначается через 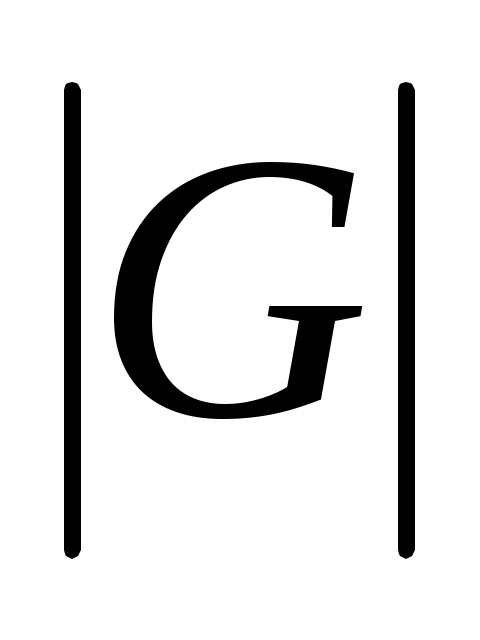. Если , то 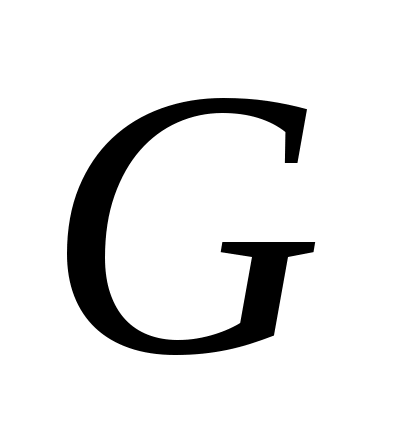называют (n, m)-графом.

Говорят, что две вершины uи vграфа смежны, если множество {и, v}является ребром, и не смежны в противном случае. Если e= {и, v}— ребро, то вершины uи vназывают его концами. В этой ситуации говорят также, что ребро e соединяет вершины uиv. Такое ребро обозначается символом uv.

Два ребра называются смежными, если они имеют общий конец.

Вершина uи ребро eназываются инцидентными, если vявляется концом ребра

---

e(т. е. e = иv), и не инцидентными в противном случае.

Заметим, что смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.

Г
рафы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. При этом точки соответствуют вершинам графа, а соединяющие пары точек линии — ребрам. В качестве иллюстрации рассмотрим граф G, изображенный на рис. 1.1. Это (5, 6)-граф, VG = {1, 2, 3, 4, 5}, EG = {{1, 2}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {4, 5}}.

Вершины 1 и 2 смежны, а 1 и 3 не смежны. Вершина 1 и ребро {1, 2} инцидентны.

Приведем примеры некоторых графов специального вида.

Граф Gназывается полным, если любые две его вершины смежны, т. е. EG=(VG)⁽²⁾. Полный граф порядка nобозначается символом K_n, число ребер в нем равно . На рис. 1.2 изображены графы K_n, n <= 5.

Граф называется пустым, если в нем нет ребер. Пустой граф порядка nобозначается через O_n.

Матрицы, ассоциированные с графом

Далее элемент матрицы M, занимающий позицию (i, j), обозначается символом M_ij. Матрица, каждый элемент которой равен 0 или 1, называется бинарной.

Пусть G— помеченный граф порядка n, VG ={1, 2, ..., n}. Определим бинарную n*n-матрицу A=A(G), положив

---

Смотрите также файлы

• По учебному курсу Управление бизнеспроцессами.docx

• 90к3ушоацсвш9щ0льацувысш0щлзпкьавм 90к3ушоацсвш9щ0льацувысш0щлзпкьавм 90к3ушоацсвш9щ0льацувысш0щлзпкьавм.docx

• Что такое Земский собор, каким был его состав.docx

• Закона 323 от 21. 11. 2011 Об основах охраны здоровья граждан в Российской Федерации.docx

• Несмотря на разногласия источников, считается, что Рим был захвачен этрусской армией примерно в 509 году до н э. в рамках свержения Тарквиния Гордого.pptx