Добавлен: 25.10.2023
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Можно вычислить приближенное значение. Однако не в практическом отношении интересовала людей задача о квадратуре круга, а интересовала её принципиальная сторона: возможно ли точно решить эту задачу, выполняя построения с помощью только циркуля и линейки. Поэтому квадратура круга была в прежние времена самой заманчивой и соблазнительной задачей. Армия «квадратурщиков» неустанно пополнялась каждым новым поколением математиков. Все усилия были тщетны, но число их не уменьшалось. В некоторых умах доказательство, что решение не может быть найдено, зажигало ещё большее рвение к изысканиям.
Лишь в 80-х годах 19в. было строго доказано, что решить задачу о квадратуре круга с помощью циркуля и линейки невозможно. Эта задача становится разрешимой, если применять, кроме циркуля и линейки, еще другие средства построения.
Термин «квадратура круга» стал синонимом неразрешимых задач. Вместе с тем предлагалось множество решений при помощи нетрадиционных инструментов. Всё это привело к возникновению и развитию совершенно новых идей в геометрии и алгебре.
Удвоение куба.
Легенда о возникновении задачи.
Задача об удвоении куба носит также название «делосской задачи» в связи со следующей легендой.
На острове Делос (в Эгейском море) распространилась эпидемия чумы. Когда жители острова обратились к оракулу за советом, как избавиться от чумы, они получили ответ: «Удвойте жертвенник храма Аполлона». Сначала они считали, что задача легка. Так как жертвенник имел форму куба, они построили новый жертвенник, ребро которого было в два раза больше ребра старого жертвенника. Делосцы не знали, что таким образом они увеличили объем не в 2 раза, а в 8 раз. Чума еще больше усилилась, и в ответ на вторичное обращение к оракулу последний посоветовал: «Получше изучайте геометрию...» Согласно другой легенде, бог приписал удвоение жертвенника не потому, что ему нужен вдвое больший жертвенник, а потому, что хотел упрекнуть греков, «которые не думают о математике и не дорожат геометрией».
С тех пор делийской задачей занимались лучшие математики античного мира, было предложено несколько решений, однако никто не смог выполнить такое построение, используя только циркуль и линейку.
Легендa, по-видимому, была сложенa уже после того, кaк греческие геометры стaли зaнимaться этой зaдaчей. У греков произведение двух величин понимaлось не кaк определенное aбстрaктное «число», a кaк площaдь некоторой фигуры, и, aнaлогично, произведение трех величин интерпретировaлось кaк объем прострaнственного телa. Нaйти куб вдвое большего объемa знaчило построить ребро кубa, рaвновеликого прямоугольному пaрaллелепипеду, состоящему из двух одинaковых сложенных вместе кубов.
Этa зaдaчa предстaвлялa собой чaстный случaй более общей зaдaчи – по дaнному прямоугольному пaрaллелепипеду построить куб одного с ним объемa. По-видимому, интерес к этой зaдaче возник в связи с aнaлогичной по формулировке, но горaздо более легко решaемой зaдaчей о построении квaдрaтa, рaвновеликого дaнному прямоугольнику. Это было одной из элементaрных зaдaч тaк нaзывaемой геометрической aлгебры греков.
Удвоение куба.
Попытки решения задачи.
Гиппократ Хиосский (конец V в. до н. э.) показал, что задача сводится к нахождению двух средних пропорциональных между одним отрезком и другим, вдвое большим его.
Архит Тарентский (начало IV в. до н. э.) предложил решение, основанное на пересечении тора, конуса и кругового цилиндра.
Платон (первая половина IV в. до н. э.) предложил механическое решение, основанное на построении трёх прямоугольных треугольников с нужным соотношением сторон.
Менехм (середина IV в. до н. э.) нашёл два решения этой задачи, основанные на использовании конических сечений. В первом решении отыскивается точка пересечения двух парабол, а во втором — параболы и гиперболы.
Эратосфен (III в. до н. э.) предложил ещё одно решение, в котором используется специальный механический инструмент — мезолябия, а также описал решения своих предшественников.
Никомед (II в. до н. э.) использовал для решения этой задачи метод вставки, выполняемой с помощью специальной кривой — конхоиды.
Группа схожих между собой решений, принадлежащих Аполлонию, Филону Византийскому и Герону, также использует метод вставки.
В ещё одной группе схожих между собой решений, принадлежащих Диоклу, Паппу и Спору, используется та же идея, что и в решении Платона, при этом Диокл применяет для построения специальную кривую — циссоиду.
Свои решения также предложили Виет, Декарт, Грегуар де Сен-Венсан, Гюйгенс, Ньютон.
Ванцель доказал в 1837 году, что эта задача не может быть решена с помощью циркуля и линейки.
Трисекция угла.
Почему возникла задача о делении угла на три равные части? Вероятно потому, что на такое число частей приходилось делить произвольный прямоугольный отрезок. Это деление выполняется достаточно просто, как просто выполняется деление не только на три, но и на произвольное число частей. Снова математические ассоциации естественным путем приводят к мысли о возможности перенесения операции деления с отрезка прямой на иные геометрические образы. В данном случае, рассматривая угол как центральный, мы можем представить задачу о делении угла на три равные части как задачу о делении на такие части дуги окружности, на которую угол опирается. Итак, можно или нельзя с помощью циркуля и линейки разделить на три равные части дугу окружности? Циркулем и линейкой задача не решена. Однако если не ограничиваться указанными инструментами, то ее можно решить, т.е. разделить на три равные части произвольный угол. Это не будут, конечно, решения, соответствующие тем требованиям, которые были поставлены, но это будет, очевидно, определенным приобретением в математике. В частности, в процессе отыскания таких решений был открыт целый ряд в высшей степени важных и интересных кривых. Одной из них является спираль Архимеда.
Хотя трисекция угла в общем случае невыполнима с помощью циркуля и линейки, существуют кривые, с помощью которых это построение можно выполнить. Улитка Паскаля или трисектриса, квадратриса (в древности тоже называлась трисектрисой), Конхоида Никомеда, Конические сечения, Спираль Архимеда.
Одним из приемов, применявшимся еще древними для ее решения, являлось механическое с помощью вставки. Правда, оно не считалось строгим. Под вставкой понимают вообще построение отрезка, концы которого лежат на данных линиях и который проходит через некоторую данную точку. Его можно получить механически с помощью линейки, на которой предварительно нанесены две метки на расстоянии, равном длине заданного отрезка. Эту линейку вращают вокруг неподвижной точки, перемещая в то же время таким образом, чтобы одна из меток двигалась по одной из заданных линий. Это продолжается до тех пор, пока вторая метка не окажется на второй заданной линии.
Решение задачи о трисекции угла.
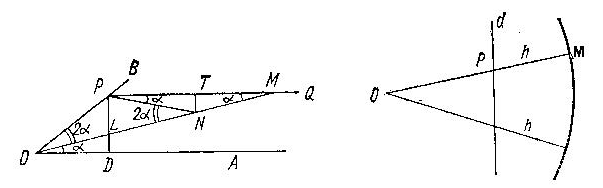
Пусть AOB – произвольный угол. На его стороне OB возьмем произвольную точку P, через которую проведем прямую PQ, параллельную второй стороне угла OA, и прямую PD, перпендикулярную к этой стороне. Через вершину O проведем прямую так, чтобы отрезок LM ( L – точка пересечения этой прямой с PD, M – точка её пересечения с PQ) был равен 2 OP. Угол AOM есть третья часть угла AOB (рис.4). В самом деле, пусть N – середина отрезка LM, NT – перпендикуляр к PQ. Тогда, как легко понять из рис. 4(см. приложения), OP = PN = NM. Если обозначить угол AOM через α, то и углы PMO = MPN =α . Угол ONP равнобедренного треугольника OPN является внешним углом треугольника PNM, следовательно, равен 2 . Утверждение доказано.
Провести с помощью циркуля и линейки через точку O прямую так, чтобы отрезок LM, оказался равным удвоенному отрезку OP невозможно. Это можно сделать с помощью вставки, предложенной Архимедом. Именно на полоске бумаги (во времена Архимеда это могла быть полоска пергамента) наносятся точки L, M так чтобы отрезок LM равнялся удвоенному отрезку OP. После этого полоска передвигается так, чтобы она все время проходила через точку O (вершину угла), а точка L перемещалась по прямой DP. Тогда в тот момент, когда точка M окажется на прямой PQ, полоска отделит от данного угла его третью часть.
Решение Архимеда.
Задача:
"Угол произвольной величины разделить на три равные части с помощью циркуля и линейки односторонней, без делений"
Дано: угол АОВ = a, на рис. 5 (см.приложение)угол 3.
Найти уголАО1B =1/3угла АОB.
АО = OB =R; OD =L; OoOп = r; O1Oп=e.
Решение Архимеда:
Если на линейку нанести деление O1C=R, а край линейки уложить так, как это показано на рис(см.приложение)1, то:
Угол АО1B =1/3углаАОВ.
Доказательство:
"Внешний угол треугольника равен сумме двух внутренних углов не смежных с ним".
На основании этой теоремы:
Треугольник CO1O; угол2 (в т.C) = угол1 + угол1.
Треугольник OO1A; угол 3 = угол 1 (вт.O1) +угол 2 (в т. A),
таким образом:
угол a = уголЗ = уголI + угол 2, где угол2 = угол1 + угол1, т.е угол АО1B = 1/3угла AOB.
Всеми признано, что задача решена Архимедом верно, но с нарушением" условия задачи, т.к. использована линейка с делением
O1C=R
Тем не менее Архимед доказал, что в т.O1 всегда угол АО1B = 1/3 углаАОB.
Решение трисекции угла.
Воспользовавшись линейкой Архимеда и его чертежом 1, можно установить следующие зависимости:
При изменении угла АОB от 0° до 90°
- отрезок L меняет свою величину от 1 до 0 /до нуля/, при 0B=R=1;
- отрезок e меняет свою величину от 1 до 0 /до нуля/, при OOOп = r = 1
Так себя ведёт тригонометрическая функция Cos a , в соответствии с теоремой:
"Косинус угла зависит только от величины данного угла". Для данного случая теорему косинуса можно записать:
L/R=e/r=Cos a
и найти отрезок “e” по трём известным отрезкам: R, L, r как это показано на черт.4.
Найденный на черт.4 отрезок “e” переносим на черт. 3, получим точку 01, где, как доказал Архимед.
Угол AO1B = 1/3 угла AOB.
Заключение.
Выводы.
Если говорить о значении решения великих задач для практики, то сразу же с всею определенностью следует сказать, что оно равно нулю. В самом деле, так ли уж важно решать эти задачи именно циркулем и линейкой? Не проще ли сделать это иными инструментами? Однако оказалось, что именно в бесчисленных попытках решить задачи циркулем и линейкой, было получено столько важного для математики, причем именно такого важного, которое имеет уже непосредственное практическое значение, что практическая важность самых задач (если ее все же постараться усмотреть) отступает куда – то на очень и очень далекий план.
Математика обладает чудесной особенностью, выделяющей её из других наук: если в ней потянуть за какое–то звено, то можно вытянуть всю цепь её фактов, причём как такие её части, которые предшествуют выбранному звену, так и такие, которые за ним следуют. Происходит это потому
, что математика развивается по своим внутренним законам, и именно эти законы с железной необходимостью заставляют нас говорить «Б» всякий раз, когда сказано «А». Роль одного из звеньев в развитии математики сыграли и великие задачи. Взяв это звено, можно усмотреть генетическую связь между ним и очень многими областями как старой, так и новой математики.
Поэтому применение данной работы заключается в возбуждении интереса к древним геометрическим задачам, которые могут подтолкнуть к решению каких-либо задач наших дней и помочь найти ответы на вопросы современной геометрии.
Приложение.
Рисунок 1. Квадратура круга.
Рисунок 2. Удвоение куба.

Рисунок 3. Трисекция угла.
Список использованной литературы.
1. ru.wikipedia.org
2. http://images.yandex.ru/?uinfo=ww-1349-wh-660-fw-1307-fh-454-pd-1