- между коэффициентом несчастных случаев (К_с.и) и количеством обученных по охране труда в организациях (е);

- между числом дней нетрудоспособности (N) и количеством обученных по охране труда в организациях (е);

- между числом пострадавших со смертельным исходом (m₂) и количеством обученных по охране труда в организациях (е).

2. 
   Проверка значимости коэффициента корреляции с помощью критерия Стьюдента.
   

Критические значения t_кр(α;k) при заданном уровне значимости α и заданном числе степеней свободы k=n-2 находятся в таблице распределения Стьюдента.

Для данного случая k=n-2=13-2=11 при заданном уровне значимости α=0,05 критическое значение t_кр=2,201.

Опытное значение критерия Стьюдента вычисляется по следующей формуле:

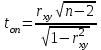. (11)

Таблица 13 - Вычисленные значения критерия Стьюдента

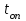	L	S	d	е	I	V	Vp
m1	14,87	-5,32	-6,48	-2,48	-7,81	-8,77	-9,91
m2	9,17	-5,03	-4,42	-2,04	-4,52	-5,06	-5,52
m3	5,96	-4,14	-8,84	-3,46	-12,76	-13,61	-16,13
N	6,83	-3,66	-4,07	-2,16	-4,03	-5,00	-5,11
Kч	9,22	-5,61	-8,43	-2,84	-9,45	-12,17	-15,27
Kл	5,95	-4,82	-4,04	-1,94	-3,71	-4,23	-4,62
Kп.з.	2,94	-2,70	-6,02	-4,08	-6,49	-6,58	-6,73
Kт	-5,71	5,09	7,99	2,58	8,61	8,48	8,90

---

Если 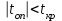, случайные величины X и Y с вероятностью p=1-α следует считать независимыми.

Если 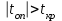, случайные величины X и Y связаны линейной корреляционной зависимостью.

Следующие величины следует считать независимыми, так как не удовлетворяют неравенству :

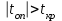- число пострадавших со смертельным исходом (m₂) и количество обученных по охране труда в организациях (е);

- коэффициент частоты смертельных исходов (К_с.и.) и количество обученных по охране труда в организациях (е);

- число дней нетрудоспособности (N) и количество обученных по охране труда в организациях (е).
Корреляционно-регрессионный анализ

Принятие решений на основе анализа опытных данных опирается на использование вероятностных законов распределения и корреляционно-регрессионного анализа. В отдельных случаях анализ опытных данных дает основания предположить, что между некоторыми из выборочных совокупностей существует определенная зависимость.

Отличие от нуля коэффициента корреляции r_xy двух случайных величин X и Y означает, что эти две величины связаны линейной зависимостью и можно ставить вопрос о поиске вида этой зависимости. Соответствующее уравнение, описывающее функциональную зависимость величины Y от величины X, называется уравнением регрессии величины X на случайную величину Y.

Уравнение регрессии, построенное по выборочным совокупностям опытных данных, позволяет с определенной вероятностью прогнозировать поведение генеральных совокупностей исследуемых величин в рамках некоторого горизонта прогноза и может быть использовано для расчетов с целью принятия решений на основе установленных закономерностей.
Уравнения множественной регрессии

В условиях данной задачи будет рассматриваться уравнение множественной регрессии. Для обнаружения значимой статистической зависимости между случайными величинами

---

Y, X₁, X₂, …, X_n ставится задача отыскания вида этой зависимости.

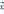
В общем случае зависимость ищется в виде функции n переменных: y=f(x₁, x₂, …, x_n). Здесь 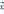=(x₁, x₂, …, x_n) – n-мерная случайная величина, y – значение функции f(x₁, x₂, …, x_n). Функцию y=f(x₁, x₂, …, x_n) требуется определить так, чтобы при каждом из значений аргумента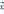 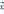=(x₁, x₂, …, x_n) значение функции f(x₁, x₂, …, x_n) было максимально приближено к соответствующему значению случайной величины Y.

Функция f предполагается линейно зависящей от своих аргументов и уравнение регрессии ищется в виде:

y = a₀ + a₁x₁ +…+a_jx_j +…+ a_nx_n. (12)

Для нахождения неизвестных параметров a₀, a₁,…, a_n функции необходимо решить следующую систему уравнений:










……………………………………………………………………………..



………………………………………………………………………………..

---

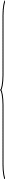
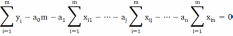
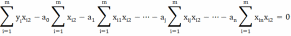
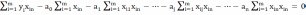
В условиях данной задачи была выбрана система уравнений с тремя неизвестными:


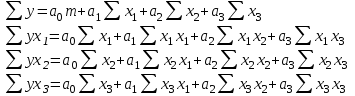
где у – значения показателей производственного травматизма и профессиональной заболеваемости (К_ч, К_л., К_п.з., К_т);

m – объем выборки, для данного случая m=13;

x_1, x_2, x₃ – показатели, которые были выбраны, исходя из результатов проверки значимости парных коэффициентов корреляции.

В уравнении для коэффициента частоты травматизма К_ч:

- x₁ – средства, израсходованные на мероприятия по охране труда в расчете на одного работающего (S);

- x₂ – инвестиции в основной капитал в фактически действовавших ценах (I);

- x₃ – валовой региональный продукт (V).

В уравнении для коэффициента частоты смертельных исходов К_л.:

- x₁ – средства, израсходованные на мероприятия по охране труда в расчете на одного работающего (S);

- x₂ – инвестиции в основной капитал в фактически действовавших ценах (I);

- x₃ – валовой региональный продукт (V).

В уравнении для коэффициента частоты профессиональных заболеваний К_п.з.:

- x₁ – валовой региональный продукт (V);

- x₂ – средства, израсходованные на мероприятия по охране труда в расчете на одного работающего (S);

- x₃ – инвестиции в основной капитал в фактически действовавших ценах (I).

В уравнении для коэффициента тяжести К_т:

- x₁ – доля работников, занятых в условиях, не отвечающих санитарно-гигиеническим нормам, от общего числа работающих (d);

- x

---

₂ – средства, израсходованные на мероприятия по охране труда в расчете на одного работающего (S);

- x₃ – валовой региональный продукт (V).

Система уравнений для коэффициента частоты производственного травматизма (К_ч):

5 2,4 = 13a₀ + 61259,9a₁ + 482,8a₂ + 2635,1a₃

208006,3= 61259,9a₀ + 398462769,9a₁ + 2854899,2a₂ + 15804692,9a₃

1663,9= 482,8a₀ + 2854899,2a₁ + 22730,3a₂ + 123312,3a₃

9060,1= 2635,1a₀ + 15804692,9a₁ + 123312,3a₂ + 674761,3a₃

Система уравнений для коэффициента частоты смертельных исходов (К_л):

1 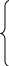,00 = 13a₀ + 61259,9a₁ + 482,8a₂ + 2635,1a₃

3859,3 = 61259,9a₀ ++ 398462769,9a₁ + 2854899,2a₂ + 15804692,9a₃

32,1 = 482,8a₀ + 2854899,2a₁ + 22730,3a₂ + 123312,3a₃

173,6= 2635,1a₀ +15804692,9a₁ + 123312,3a₂ + 674761,3a₃

Система уравнений для коэффициента частоты профессиональных заболеваний (К_п.з.):
1 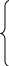6 = 13a₀ + 2635,1a₁ + 61259,9a₂ + 482,8a₃

2883,8= 2635,1a₀ +674761,3 a₁ +15804692,9 a₂ + 123312,3a₃

68475,3= 61259,9a₀ + 15804692,9 a₁ + 398462769,9a₂ + 2854899,2a₃

527,9= 482,8a₀ + 123312,3a₁ + 2854899,2a₂ + 22730,3a₃
Система уравнений для коэффициента тяжести (К_т):

4 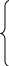33,0 = 13a₀ + 313,6a

---

Смотрите также файлы

• Влияние физической культуры и спорта на организм человека.rtf

• 1 хаттамасы маусым 2023ж саат минуттан саат минута дейін Абдрашид Ділшат лы 1304000Есептеу техникасы жне бадарламамен амтасыз ету.docx

• Организационная структура и взаимодействие подразделений организации с бухгалтерией (кассой).docx

• Организационное обеспечение (ОО).docx

• Теоретические основы организации рекламной деятельности в туристическом бизнесе.docx