Файл: Скат на матан 2023 3 сем Демидовs skats present Методичка.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 25
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Скат на матан 2023 3 сем
Демидов’s skats present
Методичка:
-
https://vk.com/doc250787250_652143923?hash=TzXIqEKFlY4gsby2NxjDpVDu9Z5zXVVCamqiQHpV4Tz&dl=4htCC7kgENFkc2YiV9CrY5kWxGlNJLLaIZ6ywRIJSj0 -1 часть -
https://vk.com/doc250787250_652143925?hash=Ckb61Ibcc3HNDij9ZCwR4RuyD9R8uzNh8HLzENNzni0&dl=tp7dMqwShHHXv52AZTz5rnCIbKggmCTnZX5KJOPSye0 – 2 часть
база из опроса – формула стокса(все 3) и ОстроградскогоГаусса
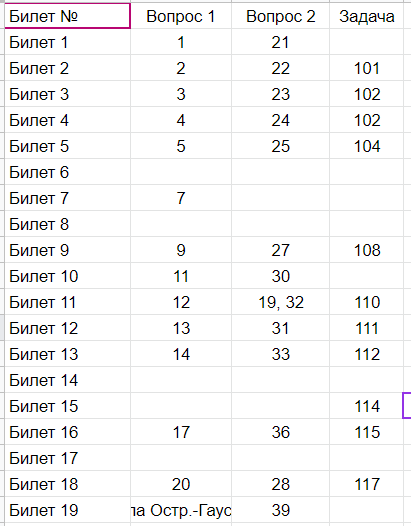
Оглавление
Билет 1 5
Вопрос 1 (Интеграл Римана на n–мерном промежутке) 5
Вопрос 21 (Касательная плоскость и нормаль к поверхности в R^3 ) 6
Задача 100 7
Билет 2 7
Вопрос 2 (Множество Лебеговой меры нуль. Критерий Лебега интегрируемости функции по Риману) 7
Вопрос 22 (Площадь поверхности в евклидовом пространстве.) 8
Задача 101 8
Билет 3 10
Вопрос 3 (Критерий Дарбу интегрируемости вещественнозначной функции) 10
Вопрос 23 (Первая квадратичная форма поверхности. Площадь поверхности в 3 R , длины кривых на поверхности.) 11
Задача 102 12
Билет 4 15
Вопрос 4 (Интеграл по множеству. Мера Жордана множества и ее геометрический смысл. Критерий Лебега существования интеграла по измеримому множеству) 15
Вопрос 24 (Алгебра форм. Кососимметрические формы. Операция внешнего умножения.) 17
Задача 103 20
Билет 5 22
Вопрос 5 (Общие свойства интеграла) 22
Вопрос 25 (Дифференциальные формы в областях евклидова пространства. Определения и примеры: дифференциал функции, форма работы, форма потока.) 23
Задача 104 23
Билет 6 25
Вопрос 6 (Сведение кратного интеграла к повторному. Теорема Фубини и следствия из нее) 25
Вопрос 26 (Координатная запись дифференциальной формы.) 26
Задача 105 26
Билет 7 28
Вопрос 7 (Замена переменных в кратном интеграле) 28
Вопрос 27 (Перенос дифференциальных форм при отображениях.) 30
Задача 106 31
Билет 8 33
Вопрос 8 (Геометрический смысл знака и модуля Якобиана отображения.) 33
Вопрос 28 (Внешний дифференциал формы.) 33
Задача 107 34
Билет 9 34
Вопрос 9 (Приложения кратных интегралов.) 34
Вопрос 27 (Перенос дифференциальных форм при отображениях.) 35
Задача 108 35
Билет 10 36
Вопрос 11 (Предел, непрерывность, дифференцируемость вектор-функции скалярного аргумента.) 36
Вопрос 30 (Форма объема. Площадь поверхности.) 37
Задача 109 39
Билет 11 39
Вопрос 12 (Параметрически заданная кривая. Касательная к кривой.) 39
Вопрос 19 (Край поверхности. Согласованная ориентация поверхности и ее края) 41
Вопрос 32 (Общая формула Стокса.) 41
Задача 110 42
Билет 12 45
Вопрос 13 (Длина дуги кривой. Натуральная параметризация.) 45
Вопрос 31 (Интегралы от дифференциальных форм 1 и 2 рода.) 46
Задача 111 46
Билет 13 47
Вопрос 14 (Естественный трехгранник кривой. Формулы Френе.) 47
Вопрос 33 (Классические интегральные формулы Ньютона-Лейбница, Стокса, ОстроградскогоГаусса.) 48
Задача 112 50
Билет 14 51
Вопрос 15 (Определение, вычисление, геометрический смысл кривизны и кручения кривой) 51
Вопрос 34 (Скалярные и векторные поля в областях евклидова пространства. Связь с дифференциальными формами) 52
Задача 113 53
Билет 15 53
Вопрос 16 (Вид кривой вблизи произвольной точки.) 53
Вопрос 35 (Дифференциальные операторы векторного анализа.) 54
Задача 114 55
Билет 16 55
Вопрос 17 (Поверхность в евклидовом пространстве. Примеры) 55
Вопрос 36 (Интегральные формулы в векторных обозначениях. Геометрическое определение div, rot.) 57
Задача 115 57
Билет 17 58
Вопрос 18 (Ориентация поверхности. Ориентируемые и неориентируемые поверхности) 58
Вопрос 37 (Потенциал векторного поля, необходимое условие потенциальности. Критерий потенциальности векторного поля.) 59
Задача 116 59
Билет 18 60
Вопрос 20 (Касательное пространство.) 60
Вопрос 28 (Внешний дифференциал формы.) 60
Вопрос 38 (Соленоидальные поля, их свойства.) 61
Задача 117 61
Билет 19 61
Вопрос 33 (Классические интегральные формулы Ньютона-Лейбница, Стокса, ОстроградскогоГаусса.) 61
Вопрос 39 (Теорема Пуанкаре. Точные и замкнутые формы.) 61
Задача 118 62
Опрос: 62
5)Остроградский (спросила что такое v с чертой), сказал, что могу ответить градиент - спросила div: 65
6)Внешний дифференциал формы - определение, его связь с ротором: 66
7)Высчитать касательную плоскость и нормаль: 67
Билет 1
Вопрос 1 (Интеграл Римана на n–мерном промежутке)
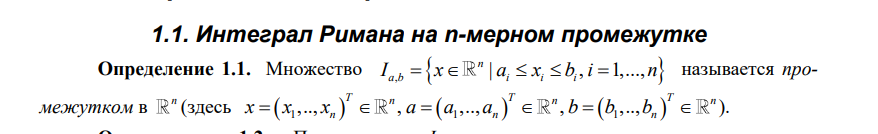

Вопрос 21 (Касательная плоскость и нормаль к поверхности в R^3 )


Задача 100
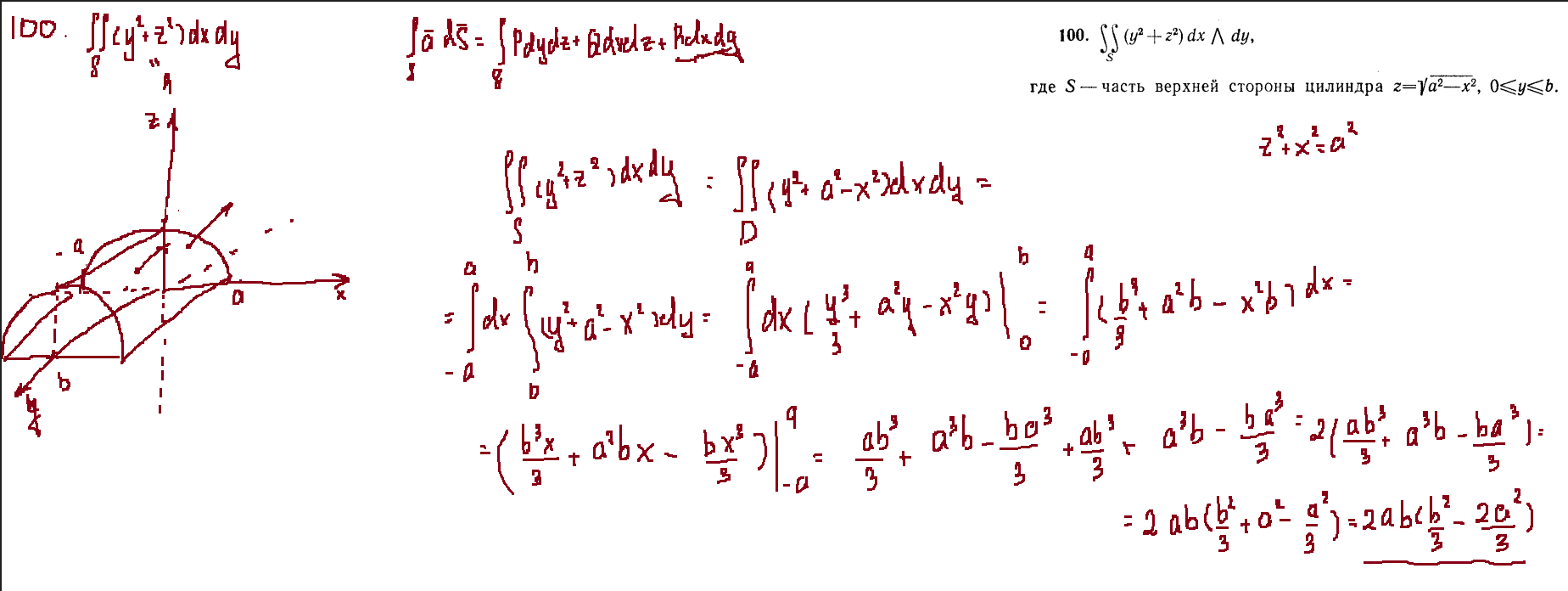
Билет 2
Вопрос 2 (Множество Лебеговой меры нуль. Критерий Лебега интегрируемости функции по Риману)


Вопрос 22 (Площадь поверхности в евклидовом пространстве.)

Задача 101
Сверху

Билет 3
Вопрос 3 (Критерий Дарбу интегрируемости вещественнозначной функции)



Вопрос 23 (Первая квадратичная форма поверхности. Площадь поверхности в 3 R , длины кривых на поверхности.)


Задача 102
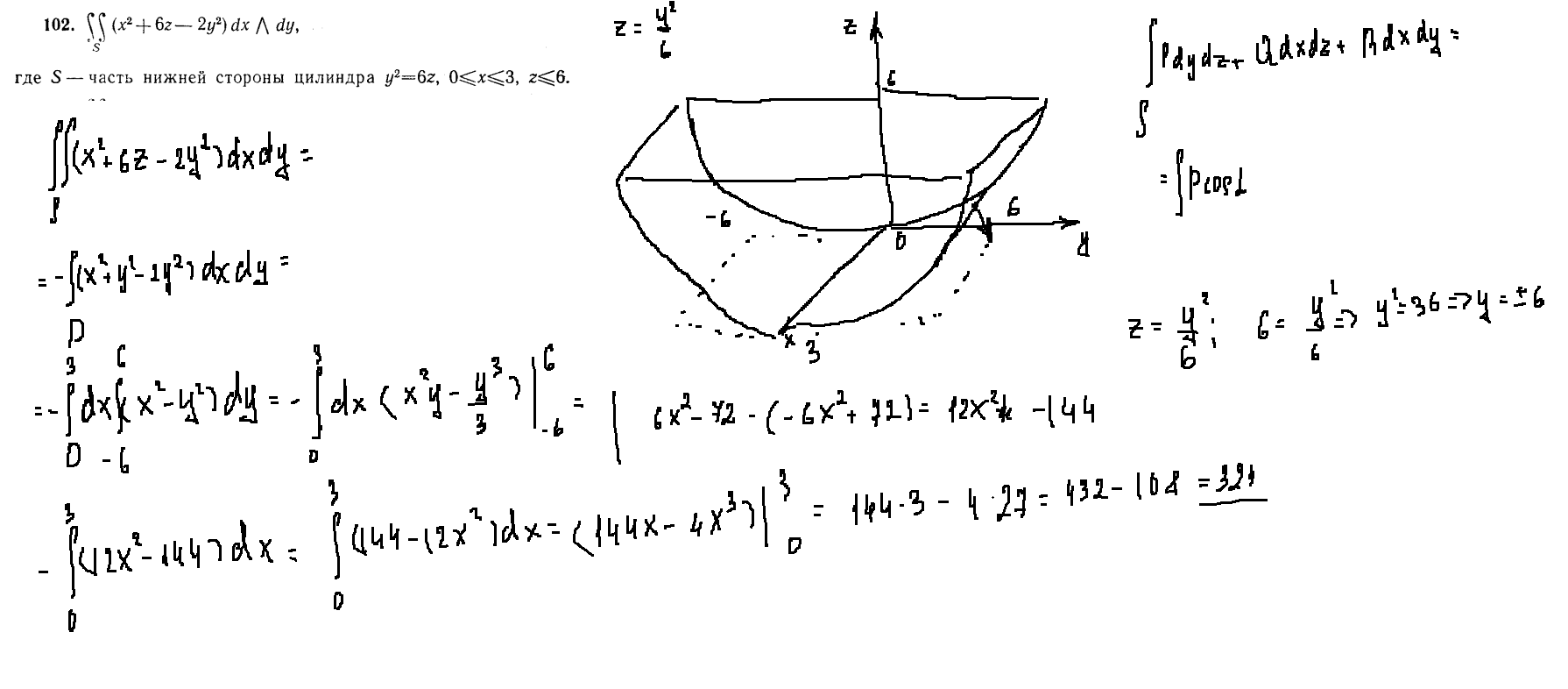 Снизу
Снизу 
Билет 4
Вопрос 4 (Интеграл по множеству. Мера Жордана множества и ее геометрический смысл. Критерий Лебега существования интеграла по измеримому множеству)
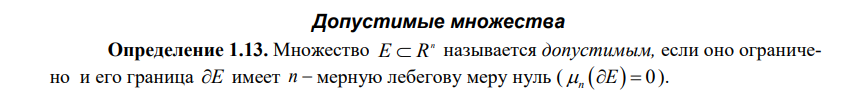
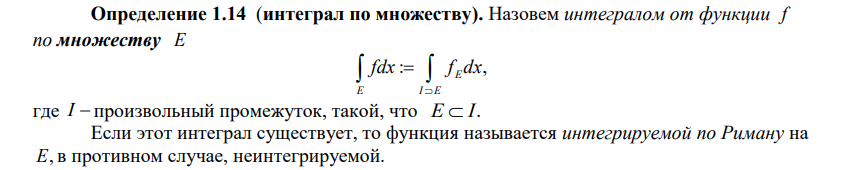


Вопрос 24 (Алгебра форм. Кососимметрические формы. Операция внешнего умножения.)




Задача 103


Билет 5
Вопрос 5 (Общие свойства интеграла)

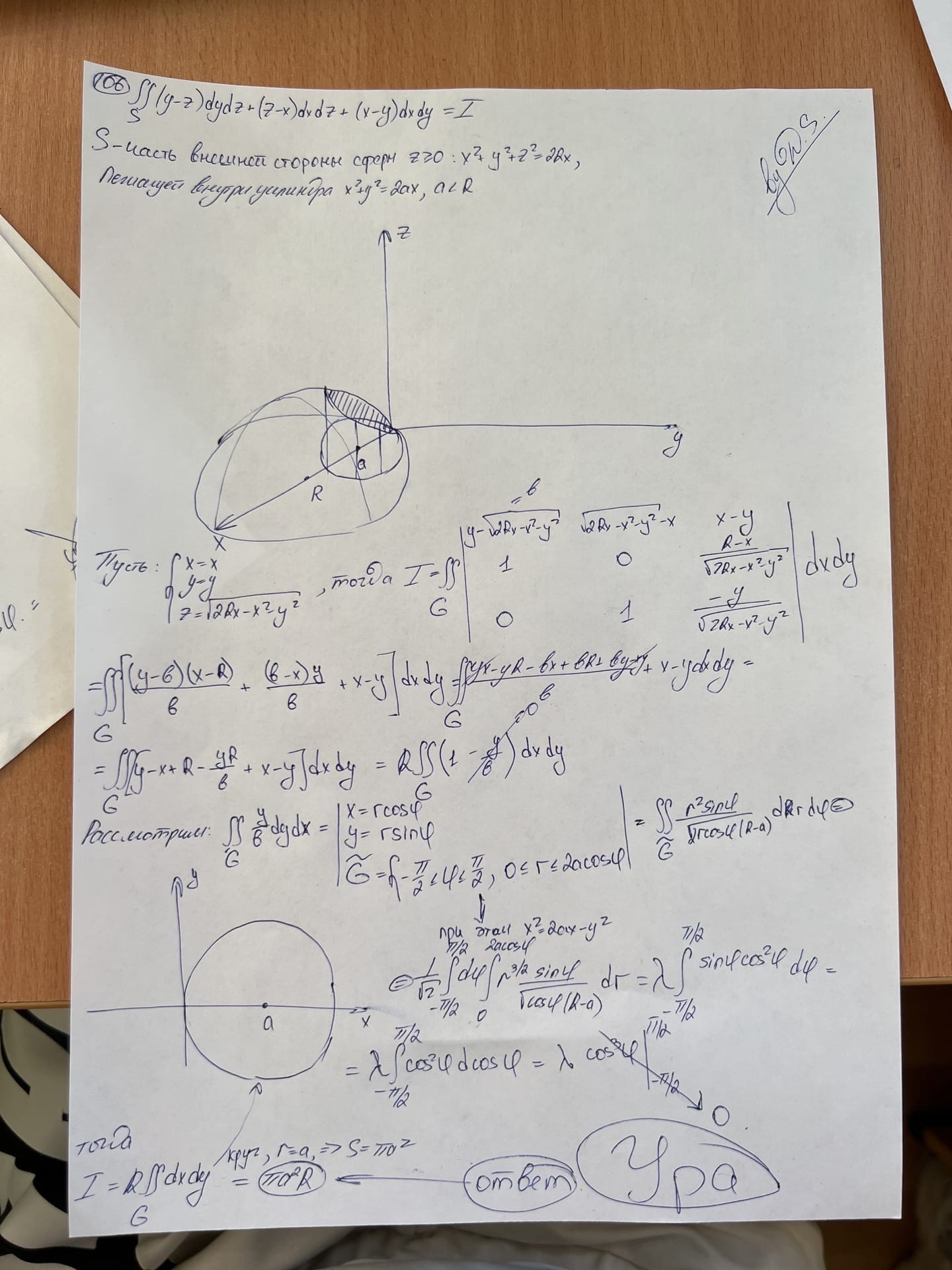
Вопрос 25 (Дифференциальные формы в областях евклидова пространства. Определения и примеры: дифференциал функции, форма работы, форма потока.)



Задача 104
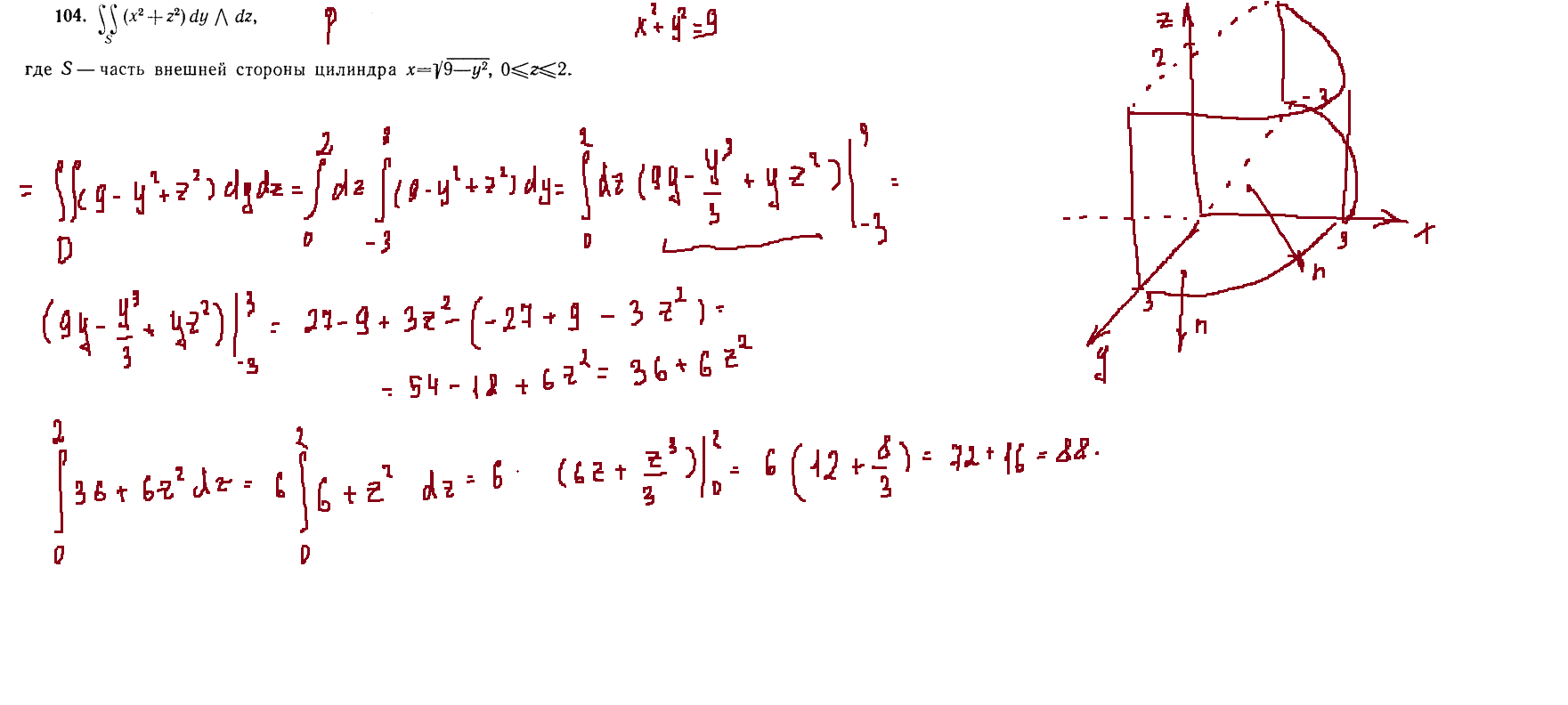
Сверху

Билет 6
Вопрос 6 (Сведение кратного интеграла к повторному. Теорема Фубини и следствия из нее)

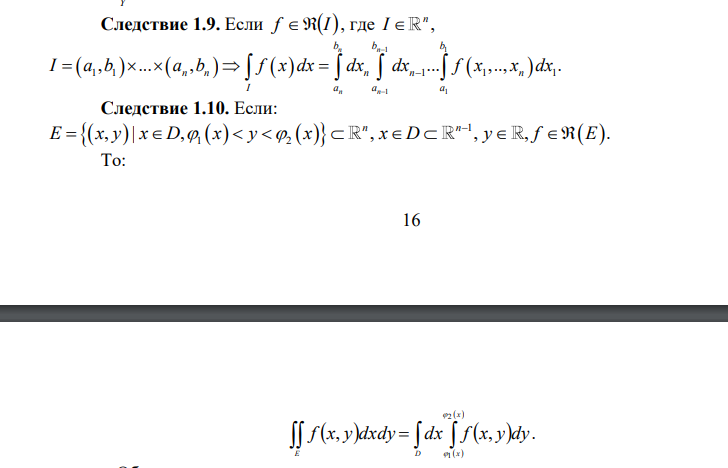
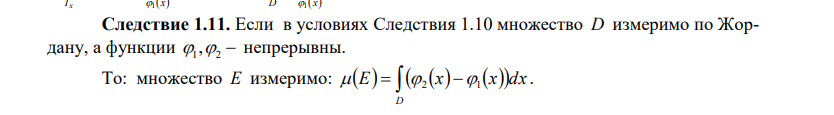
Вопрос 26 (Координатная запись дифференциальной формы.)

Задача 105

Снизу

Билет 7
Вопрос 7 (Замена переменных в кратном интеграле)



Вопрос 27 (Перенос дифференциальных форм при отображениях.)

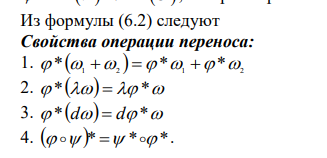
Задача 106

Билет 8
Вопрос 8 (Геометрический смысл знака и модуля Якобиана отображения.)

Вопрос 28 (Внешний дифференциал формы.)

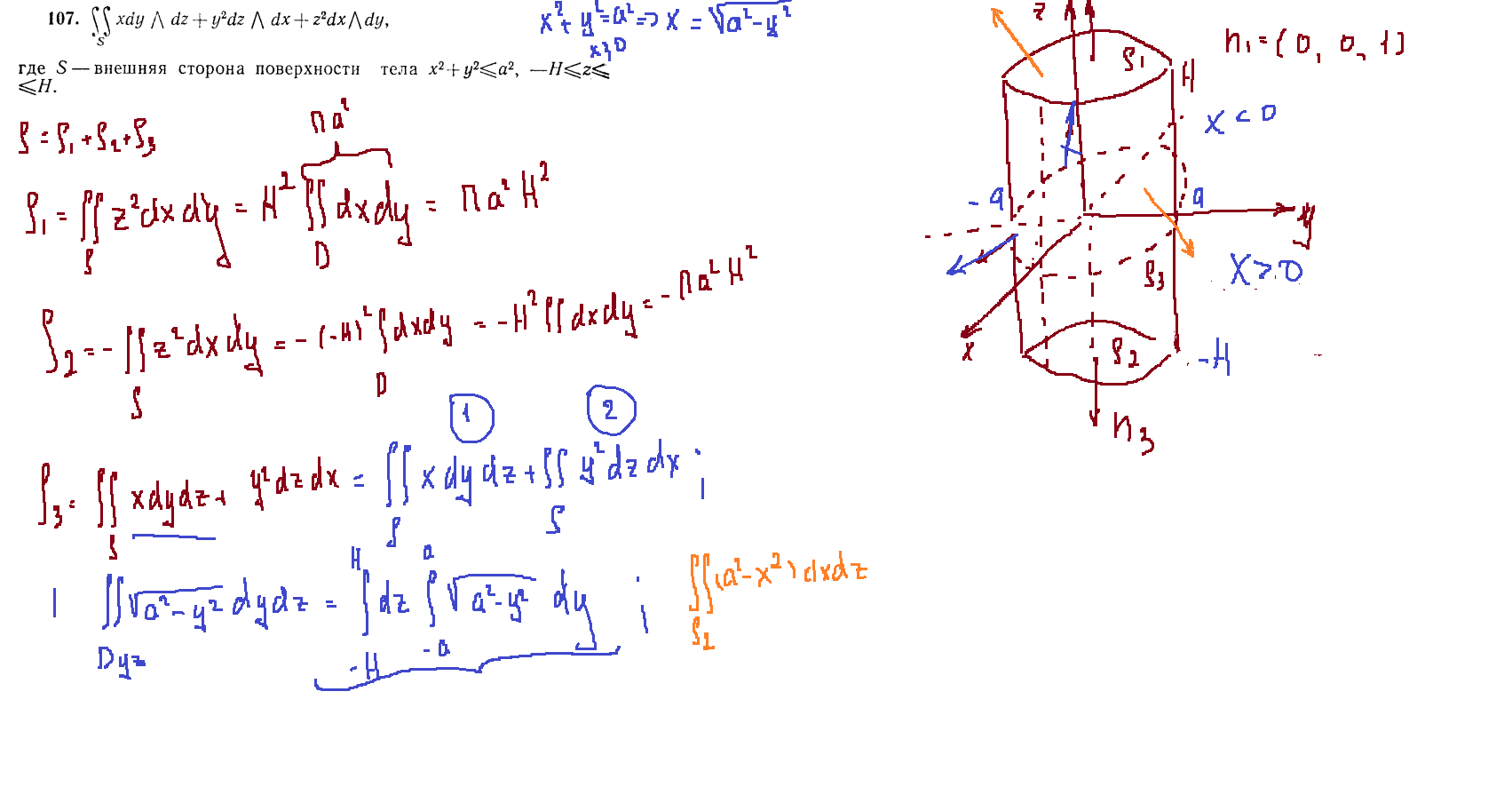
Задача 107
Билет 9
Вопрос 9 (Приложения кратных интегралов.)

Вопрос 27 (Перенос дифференциальных форм при отображениях.)

Задача 108
Пока нет
Билет 10
Вопрос 11 (Предел, непрерывность, дифференцируемость вектор-функции скалярного аргумента.)

Вопрос 30 (Форма объема. Площадь поверхности.)



Задача 109
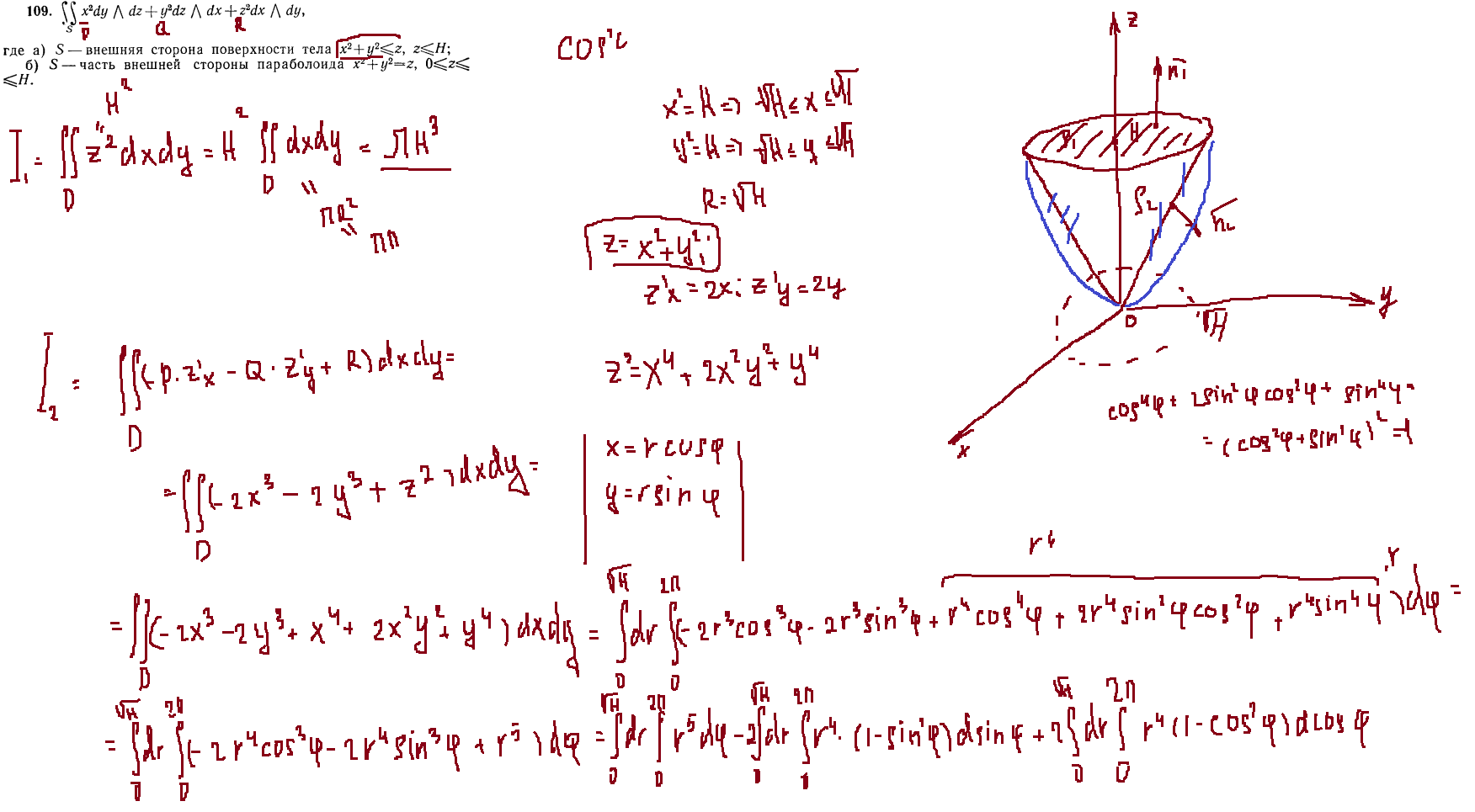
Билет 11
Вопрос 12 (Параметрически заданная кривая. Касательная к кривой.)

Вопрос 19 (Край поверхности. Согласованная ориентация поверхности и ее края)

Вопрос 32 (Общая формула Стокса.)

Задача 110
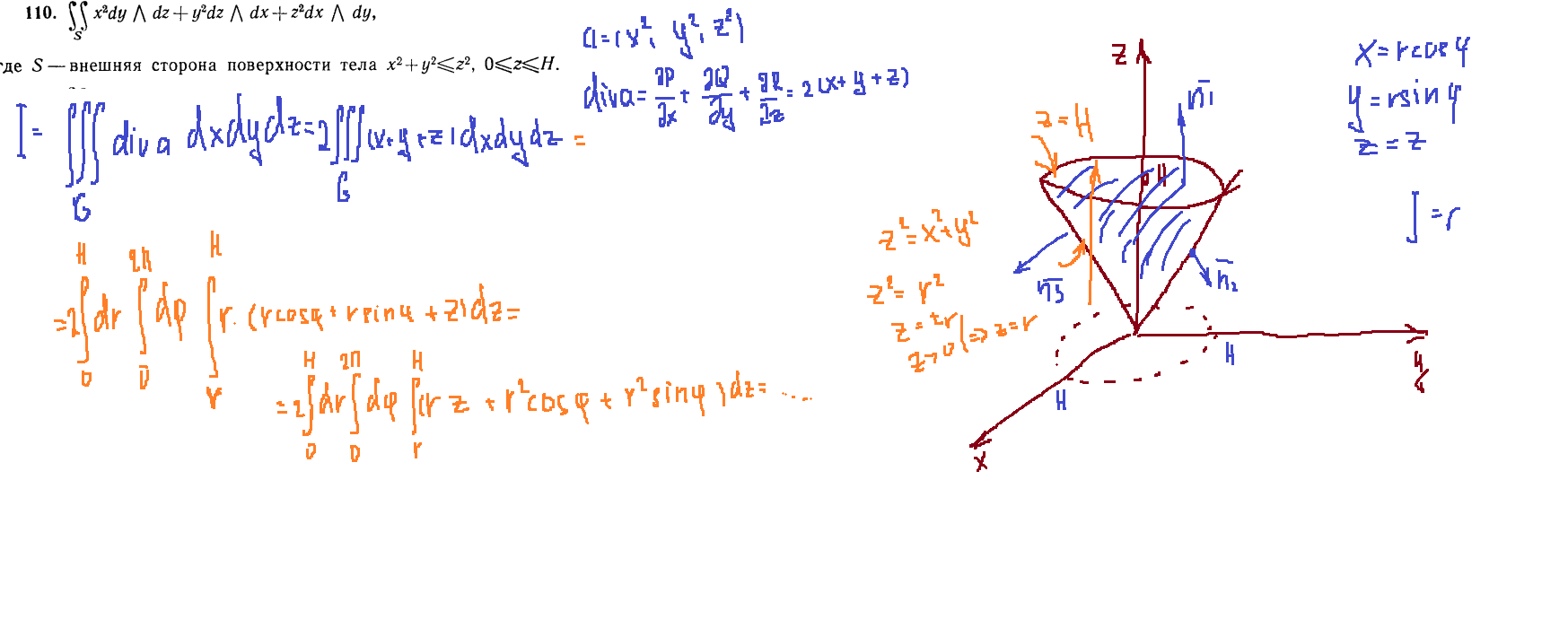

Билет 12
Вопрос 13 (Длина дуги кривой. Натуральная параметризация.)



Вопрос 31 (Интегралы от дифференциальных форм 1 и 2 рода.)

Задача 111
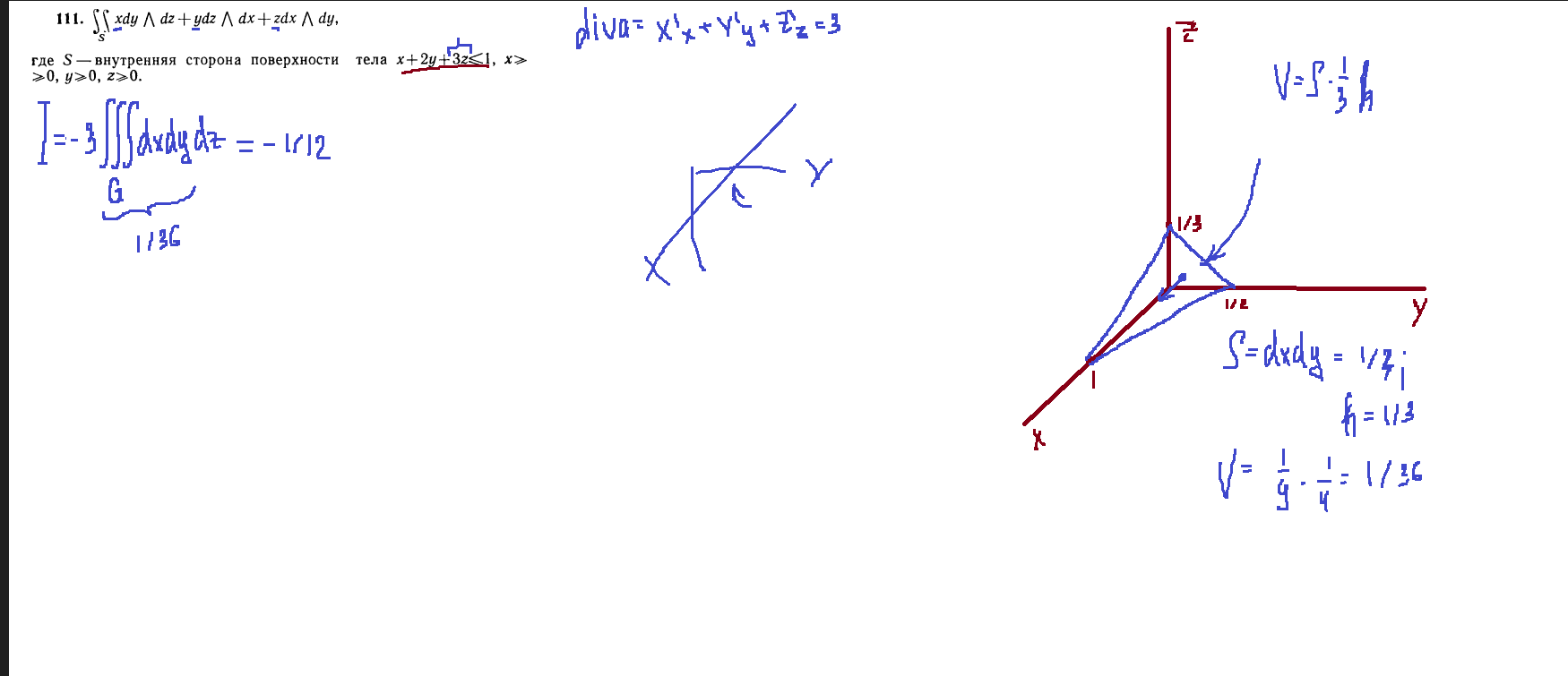
Билет 13
Вопрос 14 (Естественный трехгранник кривой. Формулы Френе.)

Вопрос 33 (Классические интегральные формулы Ньютона-Лейбница, Стокса, ОстроградскогоГаусса.)