Файл: Даны вершины А(5 3), В(11 9), С(4 15) треугольника авс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ» |
Практическое задание
| по | «Элементы высшей математики» |
дисциплине
| Выполнил(а) студент(ка) | Фатеева Ольга Викторовна | ||
| | фамилия имя отчество | ||
| Идентификационный номер: | 2201-0710-2203051 | ||
| | | ||
Пермь 2023
Задание № 1.
Даны вершины А(5; 3), В(-11; -9), С(-4; 15) треугольника АВС. Требуется
найти:
а) уравнение стороны АС;
б) длину высоты, проведенной из вершины А;
в) величину угла В (в радианах).
а) Уравнение прямой по двум точкам:
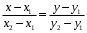
Вместо x1, x2, y1, y2 подставим координаты точек A и C:
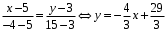
б) Найдём расстояние от точки A до прямой BC. Найдём уравнение BC по аналогии с пунктом а).
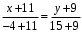
Тогда
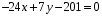
Здесь уравнение прямой записано в виде Ax + By + C = 0.
Обозначим координаты точки A через (xA, yA); точки B через (xB, yB); точки C через (xC, yC).
Расстояние от точки А(5; 3) до прямой
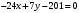вычисляется по формуле: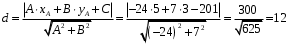
в) Величину угла B определим по формуле:
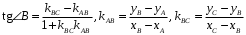
Определим коэффициенты k:
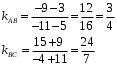
Тогда
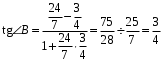
Теперь вычислим угол B через арктангенс:
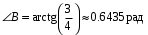
Задание № 2.
Даны вершины А1(7; 0; 3), A2(3; 0; -1), A3(3; 0; 5), A4(4; 3; -2). Средствами
векторной алгебры найти:
а) длину ребра А1A2;
б) угол между ребрами А1A2 и А1A3;
в) площадь грани А1A2A3 ;
г) длину высоты пирамиды, проведенной из вершины A4;
д) объем пирамиды А1A2A3A4.
Введём обозначения координат:
A1(x1, y1, z1), A2(x2, y2, z2), A3(x3, y3, z3), A4(x4, y4, z4).
а) Длину ребра A1A2 найдём по формуле:
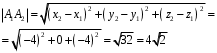
Аналогично найдём A1A3 и A2A3 для следующего пункта:
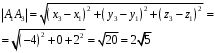
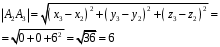
б) Угол между рёбрами А1A2 и А1A3 найдём из теоремы косинусов:
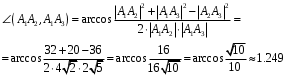
в) Вычислим площадь грани A1A2A3.
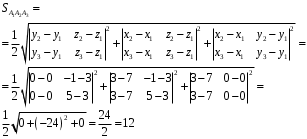
г) Найдём длину высоты пирамиды, проведенной из вершины A4. Из формулы объёма пирамиды имеем:
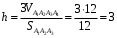
д) Объём пирамиды найдём по формуле:
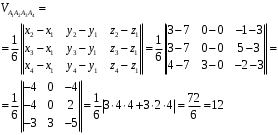
Задание № 3. Найти матрицу С = 3А – 2В, где
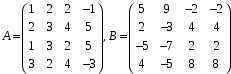
Вычислим С = 3А – 2В:
Задание №4.
Решить систему линейных алгебраических уравнений.
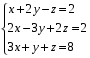(1)Решим систему методом Гаусса. Приведём систему к диагональному виду, запишем расширенную матрицу:
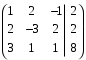
От второй строки вычтем первую строку, умноженную на 2. От третьей строки вычтем первую строку, умноженную на 3.
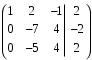
Теперь из третьей строки вычтем вторую строку
, умноженную на 5/7.
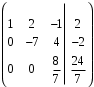
Из последнего уравнения найдём явно z. Умножим последнюю строчку на 7/8.
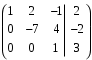
Избавимся от 4 и –1. Вычтем из второй строчки третью строчку, умноженную на 4. К первой строчке прибавим третью.
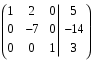
Разделим вторую строчку на –7.
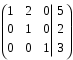
От первой строчки отнимем вторую, умноженную на 2.
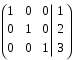
Таким образом, x = 1, y = 2, z = 3.
Проверка. Подставим в исходную систему (1) вычисленные значения:
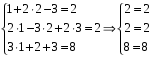
Получили верные числовые равенства. Задача решена верно.
Задание №5.
Вычислить площадь фигуры, ограниченной линиями y = x2 – 4x + 3 и y = x – 1. Построить график.
Введём функции: f(x) = x – 1; g(x) = x2 – 4x + 3.
Построим графики функций. f(x) – линейная функция, угловой коэффициент равен 1, пересекает ось ординат в торчке –1. g(x) –квадратичная функция. Вычислим координаты вершины:
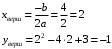
Тогда функцию g(x) можно переписать:
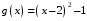
Таким образом, g(x) – стандартная парабола, смещённая на 2 единицы вправо и на одну единицу вниз.
Изобразим графики функций и определим область между графиками.
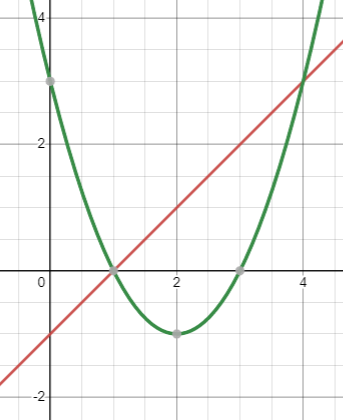
Для вычисления площади между графиками разделим пространство на несколько областей.
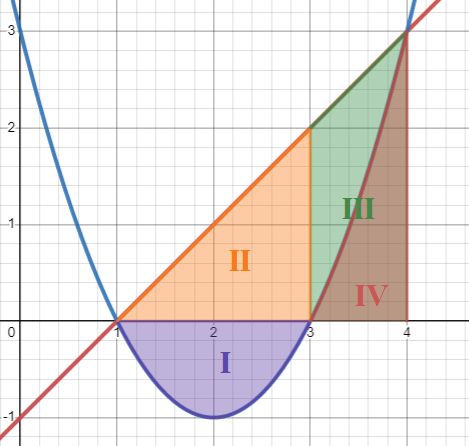
Область I – площадь между параболой и осью абсцисс, 1 < x < 3.
Область II – площадь между прямой и осью абсцисс, 1 < x < 3.
Область III – площадь между прямой и осью абсцисс, 3 < x < 4.
Область IV – площадь между параболой и осью абсцисс, 3 < x < 4.
Если вычислить интеграл для области I, получится отрицательное значение, так как график расположен ниже оси абсцисс. Поэтому вычисленное значение возьмём по модулю.
Интеграл по области II положителен, равен площади треугольника.
Из площади области III нужно отнять площадь области IV, чтобы получить необходимую часть между графиками.
Вычислим соответствующие интегралы.
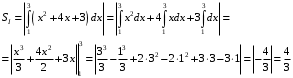
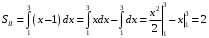
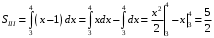
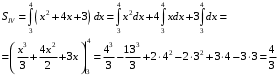
Тогда итоговая площадь равна:
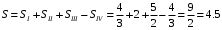
Ответ: 4.5
Задание № 6. Оптимальное планирование. Постановка задачи: предприятие располагает ресурсами сырья, рабочей силы и оборудованием, необходимым для производства любого из трех видов производимых товаров 1, 2, 3. Затраты ресурсов на изготовление единицы товара, а также запасы ресурсов указаны в следующей таблице:
Таблица 1
| Вид ресурсов | Затраты ресурса на единицу товара | Запас ресурсов | ||
| 1 | 2 | 3 | ||
| Сырье, кг | a11 | a12 | a13 | B1 |
| Рабочая сила, ч. | a21 | a22 | a23 | B2 |
| Оборудование, станко-час. | a31 | a32 | a33 | B3 |
| Прибыль, руб | P1 | P2 | P3 | |
Определить какой ассортимент товара надо выпускать, чтобы прибыль была максимальной, используя следующие данные:
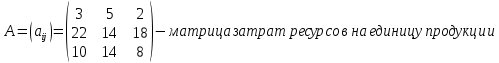
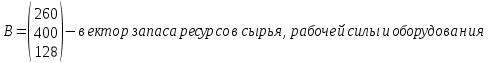
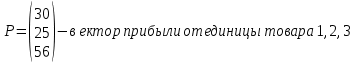
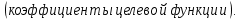
Информацию представить в виде таблицы №1, построить модель. Решить симплексным методом, проанализировать полученный результат.
Решение.
Исходную информацию представим в виде таблицы №1:
Таблица 1
| Вид ресурсов | Затраты ресурса на единицу товара | Запас ресурсов | ||
| 1 | 2 | 3 | ||
| Сырье, кг | 3 | 5 | 2 | 260 |
| Рабочая сила, ч. | 22 | 14 | 18 | 400 |
| Оборудование, станко-час. | 10 | 14 | 8 | 128 |
| Прибыль, руб | 30 | 25 | 56 | |
Обозначим х1, х2, х3 – число единиц продукции вида 1, 2 и 3 соответственно, запланированных к производству. Для их изготовления потребуется (3х1 + 5х2 + 2х3) кг. сырья, (22х1 + 14х2 + 18х3) ч. рабочей силы, (10х1 + 14х2 + 8х3) стан-час. оборудования. Потребление ресурсов не должно превышать их запасов, соответственно 260, 400 и 128 единиц.
Тогда экономико-математическую модель задачи можно сформулировать так:
Найти план выпуска продукции Х = (х1, х2, х3), удовлетворяющий системе ограничений:
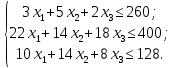
и условию х1, х2, х3 ≥ 0,
при котором функция F = 30х1 + 25х2 + 56х3 принимает максимальное значение.
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6.
3x1 + 5x2 + 2x3 + x4 = 260
22x1 + 14x2 + 18x3 + x5 = 400
10x1 + 14x2 + 8x3 +