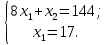Файл: Даны вершины А(5 3), В(11 9), С(4 15) треугольника авс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 37
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
x6 = 128
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
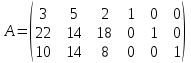
Решим систему уравнений относительно базисных переменных: x4, x5, x6. Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0, 0, 0, 260, 400, 128).
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi/ai3 и из них выберем наименьшее: min (260:2, 400:18, 128:8) = 16. Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (8) и находится на пересечении ведущего столбца и ведущей строки.
Пересчитаем симплекс-таблицу по правилу прямоугольника. Получаем новую симплекс-таблицу:
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи, который
можно записать так: x1 = 0, x2 = 0, x3 = 16.
F(X) = 30·0 + 25·0 + 56·16 = 896.
Анализ оптимального плана.
В оптимальный план вошла дополнительная переменная x4. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 1-го вида в количестве 228.
В оптимальный план вошла дополнительная переменная x5. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 2-го вида в количестве 112.
Значение 40> 0 в столбце x1 означает, что использование x1 - не выгодно.
Значение 73> 0 в столбце x2
означает, что использование x2 - не выгодно.
Значение 0 в столбце x3 означает, что использование x3 - выгодно.
Задание № 7. Графический метод. Постановка задачи: для изготовления двух видов продукции имеются три вида ресурсов, объемы которых ограничены величинами b1, b2, b3 соответственно. Расход i-го вида ресурса на изготовление одной единицы j-го вида продукции равен aij, i = 1, 2, 3, j = 1, 2. Объем выпуска каждого из видов продукции ограничен число x1* и x2* единиц, прибыль, получаемая от реализации одной единицы изготовленной продукции равна с1 и с2 соответственно. Данные задачи могут быть представлены в форме таблицы:
Требуется составить план выпуска продукции (число единиц продукции по каждому виду), удовлетворяющий принятым ограничениям и приносящий максимум прибыли после реализации выпущенной продукции, имея следующие данные:
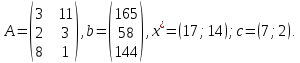
Решение.
Исходные данные:
Математическая модель задачи:
Обозначим х1, х2 – число единиц продукции вида 1 и 2, запланированных к производству. Для их изготовления потребуется (3х1 + 11х2) единиц ресурса 1, (2х1 + 3х2) единиц ресурса 2, (8х1 + х2) единиц ресурса 3. Потребление ресурсов не должно превышать их запасов, соответственно 165, 58 и 144 единиц. Объем выпуска каждого из видов продукции ограничен 17 и 14 единиц соответственно.
Тогда экономико-математическую модель задачи можно сформулировать так:
Найти план выпуска продукции Х = (х1, х2), удовлетворяющий системе ограничений:
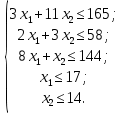
и условию х1, х2 ≥ 0,
при котором функция F = 7х1 + 2х2= 0 принимает максимальное значение.
Для графического решения задачи построим множество допустимых решений, задаваемое неравенствами-ограничениями (1) – (5):
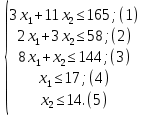
Ограничение (1) в задаче определяется прямой 3x1 + 11x2 = 165, проходящей через точки:
Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (1) получается верное неравенство: 3·0 + 11·0 ≤ 165.
Ограничение (2) в задаче определяется прямой 2x1 + 3x2 = 58, проходящей через точки:
Множество допустимых решений в задаче будет ограничено этой прямой и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (2) получается верное неравенство: 2·0 + 3·0 ≤ 58.
Ограничение (3) в задаче определяется прямой 8x1 + x2 = 144, проходящей через точки:
Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 8·0 + 0 ≤ 144.
Ограничение (4) в задаче определяется прямой x1 = 17, параллельной оси х2. Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 0 ≤ 17.
Ограничение (5) в задаче определяется прямой x2 = 14, параллельной оси х1. Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 0 ≤ 14.
Ограничения х1 ≥ 0, х2 ≥ 0 в задаче задают 1-ю четверть координатной плоскости.
Множество допустимых решений включает все точки, в которых ограничения выполняются одновременно. Отметим крайние точки получившегося множества: A, B, С, D, E.
П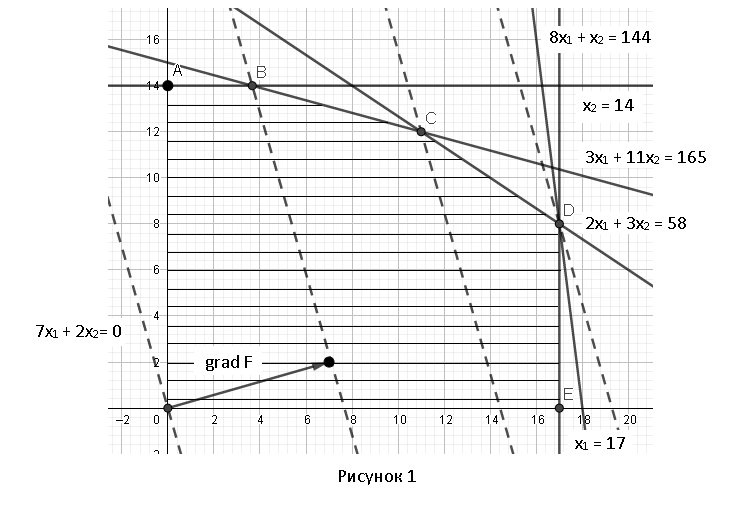
остроим градиент функции f (X) = (7, 2)Т в точке (0, 0)Т.
Построим линию уровня функции f (X) = C , проходящую через точку (0, 0)Т. Для этого найдем значение константы C , подставив координаты точки в целевую функцию: C = 7· 0 + 2· 0 = 0, и затем построим прямую 7x1 + 2x2 = 0. Построенная линия уровня перпендикулярна градиенту и пересекает множество допустимых решений.
Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации f(X).
Будем двигать эту прямую параллельным образом. Поскольку нас интересует наибольшее значение f(x), поэтому двигаем прямую до последнего касания обозначенной области. Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых:
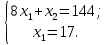
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
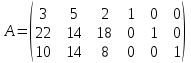
Решим систему уравнений относительно базисных переменных: x4, x5, x6. Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0, 0, 0, 260, 400, 128).
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x4 | 260 | 3 | 5 | 2 | 1 | 0 | 0 |
| x5 | 400 | 22 | 14 | 18 | 0 | 1 | 0 |
| x6 | 128 | 10 | 14 | 8 | 0 | 0 | 1 |
| F(X0) | 0 | -30 | -25 | -56 | 0 | 0 | 0 |
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi/ai3 и из них выберем наименьшее: min (260:2, 400:18, 128:8) = 16. Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (8) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | min |
| x4 | 260 | 3 | 5 | 2 | 1 | 0 | 0 | 130 |
| x5 | 400 | 22 | 14 | 18 | 0 | 1 | 0 | 200/9 |
| x6 | 128 | 10 | 14 | 8 | 0 | 0 | 1 | 16 |
| F(X1) | 0 | -30 | -25 | -56 | 0 | 0 | 0 | |
Пересчитаем симплекс-таблицу по правилу прямоугольника. Получаем новую симплекс-таблицу:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
| x4 | 228 | 1/2 | 3/2 | 0 | 1 | 0 | -1/4 |
| x5 | 112 | -1/2 | -35/2 | 0 | 0 | 1 | -9/4 |
| x3 | 16 | 5/4 | 7/4 | 1 | 0 | 0 | 1/8 |
| F(X1) | 896 | 40 | 73 | 0 | 0 | 0 | 7 |
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи, который
можно записать так: x1 = 0, x2 = 0, x3 = 16.
F(X) = 30·0 + 25·0 + 56·16 = 896.
Анализ оптимального плана.
В оптимальный план вошла дополнительная переменная x4. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 1-го вида в количестве 228.
В оптимальный план вошла дополнительная переменная x5. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 2-го вида в количестве 112.
Значение 40> 0 в столбце x1 означает, что использование x1 - не выгодно.
Значение 73> 0 в столбце x2
означает, что использование x2 - не выгодно.
Значение 0 в столбце x3 означает, что использование x3 - выгодно.
Задание № 7. Графический метод. Постановка задачи: для изготовления двух видов продукции имеются три вида ресурсов, объемы которых ограничены величинами b1, b2, b3 соответственно. Расход i-го вида ресурса на изготовление одной единицы j-го вида продукции равен aij, i = 1, 2, 3, j = 1, 2. Объем выпуска каждого из видов продукции ограничен число x1* и x2* единиц, прибыль, получаемая от реализации одной единицы изготовленной продукции равна с1 и с2 соответственно. Данные задачи могут быть представлены в форме таблицы:
| Номер ресурса | Объем ресурса (запас) | Номер продукции | |
| 1 | 2 | ||
| 1 | b1 | a11 | a12 |
| 2 | b2 | a21 | a22 |
| 3 | b3 | a31 | a32 |
| Ограничения по выпуску | x1* | x2* | |
| Прибыль | с1 | с2 | |
Требуется составить план выпуска продукции (число единиц продукции по каждому виду), удовлетворяющий принятым ограничениям и приносящий максимум прибыли после реализации выпущенной продукции, имея следующие данные:
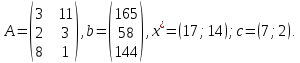
Решение.
Исходные данные:
| Номер ресурса | Объем ресурса (запас) | Номер продукции | |
| 1 | 2 | ||
| 1 | 165 | 3 | 11 |
| 2 | 58 | 2 | 3 |
| 3 | 144 | 8 | 1 |
| Ограничения по выпуску | 17 | 14 | |
| Прибыль | 7 | 2 | |
Математическая модель задачи:
Обозначим х1, х2 – число единиц продукции вида 1 и 2, запланированных к производству. Для их изготовления потребуется (3х1 + 11х2) единиц ресурса 1, (2х1 + 3х2) единиц ресурса 2, (8х1 + х2) единиц ресурса 3. Потребление ресурсов не должно превышать их запасов, соответственно 165, 58 и 144 единиц. Объем выпуска каждого из видов продукции ограничен 17 и 14 единиц соответственно.
Тогда экономико-математическую модель задачи можно сформулировать так:
Найти план выпуска продукции Х = (х1, х2), удовлетворяющий системе ограничений:
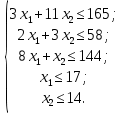
и условию х1, х2 ≥ 0,
при котором функция F = 7х1 + 2х2= 0 принимает максимальное значение.
Для графического решения задачи построим множество допустимых решений, задаваемое неравенствами-ограничениями (1) – (5):
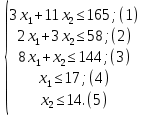
Ограничение (1) в задаче определяется прямой 3x1 + 11x2 = 165, проходящей через точки:
| x1 | x2 |
| 0 | 15 |
| 55 | 0 |
Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (1) получается верное неравенство: 3·0 + 11·0 ≤ 165.
Ограничение (2) в задаче определяется прямой 2x1 + 3x2 = 58, проходящей через точки:
| x1 | x2 |
| 2 | 18 |
| 29 | 0 |
Множество допустимых решений в задаче будет ограничено этой прямой и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (2) получается верное неравенство: 2·0 + 3·0 ≤ 58.
Ограничение (3) в задаче определяется прямой 8x1 + x2 = 144, проходящей через точки:
| x1 | x2 |
| 0 | 144 |
| 18 | 0 |
Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 8·0 + 0 ≤ 144.
Ограничение (4) в задаче определяется прямой x1 = 17, параллельной оси х2. Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 0 ≤ 17.
Ограничение (5) в задаче определяется прямой x2 = 14, параллельной оси х1. Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 0 ≤ 14.
Ограничения х1 ≥ 0, х2 ≥ 0 в задаче задают 1-ю четверть координатной плоскости.
Множество допустимых решений включает все точки, в которых ограничения выполняются одновременно. Отметим крайние точки получившегося множества: A, B, С, D, E.
П

остроим градиент функции f (X) = (7, 2)Т в точке (0, 0)Т.
Построим линию уровня функции f (X) = C , проходящую через точку (0, 0)Т. Для этого найдем значение константы C , подставив координаты точки в целевую функцию: C = 7· 0 + 2· 0 = 0, и затем построим прямую 7x1 + 2x2 = 0. Построенная линия уровня перпендикулярна градиенту и пересекает множество допустимых решений.
Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации f(X).
Будем двигать эту прямую параллельным образом. Поскольку нас интересует наибольшее значение f(x), поэтому двигаем прямую до последнего касания обозначенной области. Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых: