Решив систему уравнений, получим: x₁ = 17; x₂ = 8.

Откуда найдем максимальное значение целевой функции:

F_max (X) = 7·17 + 2·8 = 135.

Задание № 8. Транспортная задача. Постановка задачи: на складах А₁, А₂, А₃ имеются запасы продукции в количествах 180, 300, 120 т. соответственно. Потребители В₁, В₂, В₃ должны получить эту продукцию в количествах 110, 350, 140 т. соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т. продукции заданы матрицей С (ден.ед.)



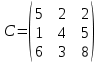
Решение.

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов:

	B1	B2	B3	Запасы
A1	5	2	2	180
A2	1	4	5	300
A3	6	3	8	120
Потребности	110	350	140

---

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 180 + 300 + 120 = 600

∑b = 110 + 350 + 140 = 600

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.

Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

Искомый элемент равен c₂₁ = 1. Для этого элемента запасы равны 300, потребности 110. Поскольку минимальным является 110, то вычитаем его.

x₂₁ = min(300, 110) = 110.

x	2	2	180
1	4	5	300 - 110 = 190
x	3	8	120
110 - 110 = 0	350	140

Искомый элемент равен c₁₂ = 2. Для этого элемента запасы равны 180, потребности 350. Поскольку минимальным является 180, то вычитаем его.

x₁₂ = min(180, 350) = 180.

x	2	x	180 - 180 = 0
1	4	5	190
x	3	8	120
0	350 - 180 = 170	140

Искомый элемент равен c₃₂ = 3. Для этого элемента запасы равны 120, потребности 170. Поскольку минимальным является 120, то вычитаем его.

x₃₂ = min(120, 170) = 120.

x	2	x	0
1	4	5	190
x	3	x	120 - 120 = 0
0	170 - 120 = 50	140

---

Искомый элемент равен c₂₂ = 4. Для этого элемента запасы равны 190, потребности 50. Поскольку минимальным является 50, то вычитаем его.

x₂₂ = min(190, 50) = 50.

x	2	x	0
1	4	5	190 - 50 = 140
x	3	x	0
0	50 - 50 = 0	140

Искомый элемент равен c₂₃ = 5. Для этого элемента запасы равны 140, потребности 140. Поскольку минимальным является 140, то вычитаем его.

x₂₃ = min(140, 140) = 140.

x	2	x	0
1	4	5	140 - 140 = 0
x	3	x	0
0	0	140 - 140 = 0

В результате получен первый опорный план, который является допустимым, так как все грузы от поставщиков вывезены, потребность потребителей удовлетворена, а план соответствует системе ограничений транспортной задачи.

	B1	B2	B3	Запасы
A1	5	2[180]	2	180
A2	1[110]	4[50]	5[140]	300
A3	6	3[120]	8	120
Потребности	110	350	140

---

Число занятых клеток таблицы (должно быть m + n – 1 = 5) 5. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 2·180 + 1·110 + 4·50 + 5·140 + 3·120 = 1730

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₂ = 2; 0 + v₂ = 2; v₂ = 2

u₂ + v₂ = 4; 2 + u₂ = 4; u₂ = 2

u₂ + v₁ = 1; 2 + v₁ = 1; v₁ = -1

u₂ + v₃ = 5; 2 + v₃ = 5; v₃ = 3

u₃ + v₂ = 3; 2 + u₃ = 3; u₃ = 1

	v1 = -1	v2 = 2	v3 = 3
u1 = 0	5	2[180]	2
u2 = 2	1[110]	4[50]	5[140]
u3 = 1	6	3[120]	8

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(1;3): 0 + 3 > 2; ∆₁₃ = 0 + 3 - 2 = 1 > 0

Выбираем максимальную оценку свободной клетки (1;3): 2. Для этого в перспективную клетку (1;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	Запасы
1	5	2[180][-]	2[+]	180
2	1[110]	4[50][+]	5[140][-]	300
3	6	3[120]	8	120
Потребности	110	350	140

---

Цикл приведен в таблице (1,3 → 1,2 → 2,2 → 2,3).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 3) = 140. Прибавляем 140 к объемам грузов, стоящих в плюсовых клетках и вычитаем 140 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

	B1	B2	B3	Запасы
A1	5	2[40]	2[140]	180
A2	1[110]	4[190]	5	300
A3	6	3[120]	8	120
Потребности	110	350	140

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.
u₁ + v₂ = 2; 0 + v₂ = 2; v₂ = 2

u₂ + v₂ = 4; 2 + u₂ = 4; u₂ = 2

u₂ + v₁ = 1; 2 + v₁ = 1; v₁ = -1

u₃ + v₂ = 3; 2 + u₃ = 3; u₃ = 1

u₁ + v₃ = 2; 0 + v₃ = 2; v₃ = 2

	v1 = -1	v2 = 2	v3 = 2
u1 = 0	5	2[40]	2[140]
u2 = 2	1[110]	4[190]	5
u3 = 1	6	3[120]	8

---

Смотрите также файлы

• Теоретические основы исследования проблемы одарённости детей в младшем школьном возрасте.docx

• Содержание. Введение Глава Понятие санкций в гражданском праве Глава Виды санкций в гражданском праве Глава Основания и условия применения гражданской правовой санкции Заключение Список использованной литературы Введение.doc

• Учебный план по направлению 44. 03. 01 Педагогическое образование.docx

• Отчет по педагогической практике информатика выполнил студент Группы, курса фио место прохождения.pdf

• Практическая работа 1 Тестирование Белым ящиком Цель работы изучить метод тестирования Белым ящиком.doc