---

Практическая работа 5

1. Как рассчитать число серий эксперимента N?

2. Чем отличается линейная модель, нелинейная модель и линейная модель со смешанными оценками?

Линейная и линейная модель со смешанными оценками требуют изменения факторов на двух уровнях, нелинейная модель – на трёх уровнях изменения факторов.

4. 
   Как оценить адекватность моделей?
   

Модель считается адекватной, если ряд остатков обладает свойствами:

• 
  независимость;
  
• 
  их случайность;
  
• 
  соответствие нормальному закону распределения;
  
• 
  равенство нулю средней ошибки.
  

					Имитационное моделирование
Планирование двухфакторного эксперимента
x1	x2	x1*x2	x1^2	x2^2		yэсперт		у1 лин			у1 лин.см.					у1 нелин.
1	1	1	1	1		11,6		12,2			20,62222					104,8889
-1	1	-1	1	1		12		12,6			4,177778					88,44444
1	-1	-1	1	1		13		12,95556			4,533333					88,8
-1	-1	1	1	1		13,6		13,35556			21,77778					106,0444
1	0	0	1	0		12,4		12,57778			12,57778					88,37778
-1	0	0	1	0		13,2		12,97778			12,97778					88,77778
0	1	0	0	1		12,8		12,4			12,4					20,86667
0	-1	0	0	1		13,2		13,15556			13,15556					21,62222
0	0	0	0	0		13,2		12,77778			12,77778					12,77778
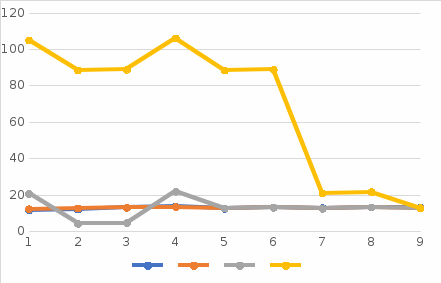
Коэффициенты моделей
а1	а2	a11	а12	а22		а0		Суммы квадратов разности
-0,2	-0,37778	75,8	8,422222	8,466667		12,77778		1,202963			281,5694					40458,99
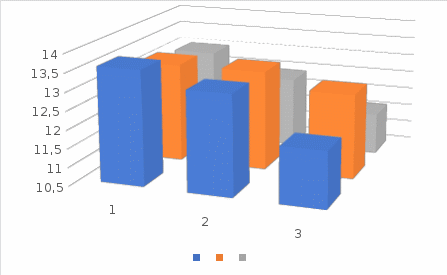
Данные для построения графика
					-1		0		1	х1
-1					13,6		13,2		12
0					13,2		13,2		12,8
1					13		12,4		11,6
х2

---

---

Практическая работа 6.

Одноканальная СМО с отказами представляет собой одну телефонную линию. Заявка-вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов 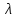=1 (вызовов в минуту). Средняя продолжительность разговоров 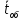=2 мин. Все потоки событий-простейшие. Определить предельные (при t→∞) значения:

1. 
   Относительной пропускной способности q
   
2. 
   Абсолютной пропускной способности А
   
3. 
   Вероятности отказа Ротк
   

Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый разговор длился в точности 2 мин, и разговоры следовали бы один за другим без перерыва.

Решение:

Определяем параметр 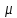потока обслуживаний:

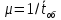=1/2=0,5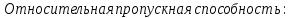





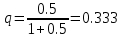
Таким образом, в установившемся режиме система будет обслуживать около 33% поступающих вызовов.

Находим абсолютную пропускную способность:



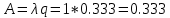
Т.е линия способна осуществить в среднем 0,333 разговора в минуту

Вероятность отказа:



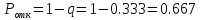
Значит около 67% поступивших вызовов будет получать отказ

Номинальная пропускная способность канала:

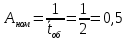разговора в минуту

Что почти вдвое больше, чем фактическая пропускная способность, получаемая, с учетом случайного характера потока заявок и случайности времени обслуживания

1. 
   Охарактеризуйте системы массового обслуживания.
   

В теории систем массового обслуживания (СМО) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.

---

Средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Например, к ним относятся каналы телефонной связи, посадочные полосы, мастера-ремонтники, билетные кассиры, погрузочно-разгрузочные точки на базах и складах.

Совокупность однотипных обслуживающих устройств называется системой массового обслуживания. Такими системами могут быть телефонные станции, аэродромы, билетные кассы, ремонтные мастерские, склады и базы снабженческо-сбытовых организаций и т.д.

Основной задачей теории СМО является изучение режима функциони­рования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслужи­вающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время без­действия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО возникают задачи оптимизации: каким образом достичь оп­ределенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с просто­ем обслуживающих устройств.

2. 
   Как рассчитать вероятность отказа?
   

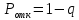
Где q-относительная пропускная способность

3. 
   Как рассчитать пропускную способность системы?
   

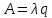
Где q-относительная пропускная способность

-интенсивность потока

4. 
   Перечислите основные элементы СМО.
   

Во всякой СМО можно выделить четыре основных элемента:

· входящий поток требований (заявок),

· очередь требований,

· каналы обслуживания,

· выходящий поток требований.

5. 
   Какие существуют показатели эффективности работы СМО?
   

---

Смотрите также файлы

• Укажите основные последовательные шаги психотерапевтической помощи по К. Роджерсу.docx

• Задания. Тема 2.docx

• Энджерикс b 1Вакцина профилактическая 3 поколения (генноинженерная) 2Антиген 3На основе поверхностного антигена гепатита В, выделенного из рекомбинантной культуры дрожжевых клеток 4Профилактика геп..docx

• Сертификация и стандартизация программного обеспечения гост 19. 10277 еспд.docx

• Волшебные моменты.docx