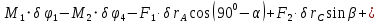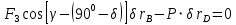ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 42
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Институт инженерной и экологической безопасности
| (наименование института полностью) |
| 20.03.01 Техносферная безопасность |
| (код и наименование направления подготовки / специальности) |
| Противопожарные системы |
| (направленность (профиль) / специализация) |
ПрактическОе заданиЕ 11,12
по учебному курсу «Механика»
| Обучающегося | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 2023
Задание 11
Дано:
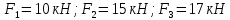
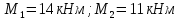
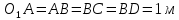
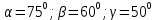
Найти:
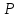
Решение

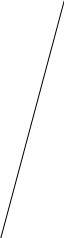

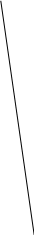


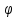
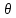







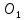
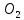



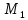
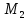
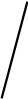

 1
1 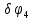
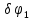 4
4 
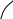
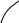
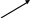
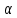
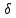
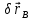
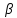
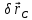







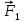
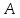
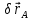
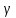
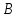
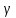
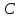
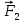
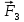 3
32




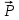
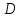
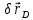
Рис. 1
Обозначим звенья механизма цифрами 1, 2, 3 и 4. Строим положение механизма в соответствие с заданными углами (рис. 1). Для решения задачи используем принцип возможных перемещений, то есть:
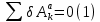
Изображаем действующие на механизм активные силы: силы
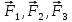
и пары сил с моментами
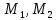 . Сообщим системе возможное перемещение. При этом стержни 1 и 4 повернутся на углы
. Сообщим системе возможное перемещение. При этом стержни 1 и 4 повернутся на углы 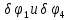 соответственно, а точки
соответственно, а точки 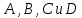 получат соответственно перемещения
получат соответственно перемещения 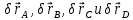 . Примем за независимое перемещение
. Примем за независимое перемещение  и определим зависимости между возможными перемещениями, учитывая, что эти зависимости такие же, как и между соответствующими скоростями. Из схемы находим:
и определим зависимости между возможными перемещениями, учитывая, что эти зависимости такие же, как и между соответствующими скоростями. Из схемы находим: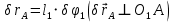
Для нахождения
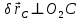 воспользуемся тем, что проекции
воспользуемся тем, что проекции  и
и  на прямую
на прямую 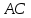 должны быть равны друг другу. Тогда
должны быть равны друг другу. Тогда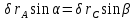
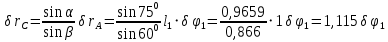
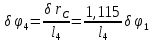
Длину звена 4 определяем из равенства:
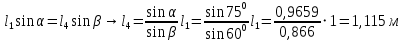
Тогда
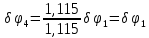
Для определения
 построим мгновенный центр скоростей (точка
построим мгновенный центр скоростей (точка  ) звена 2. Зная положение МЦС, можем записать:
) звена 2. Зная положение МЦС, можем записать: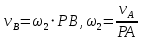
Для определения расстояния
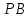 рассмотрим два треугольника
рассмотрим два треугольника 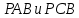 . По теореме синусов можем записать два равенства:
. По теореме синусов можем записать два равенства: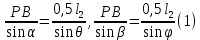
Из этих выражений следует:
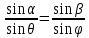
Или
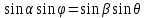
(2)
Из треугольника
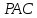 определяем:
определяем: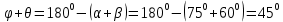
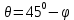
Подставляем в равенство (2):
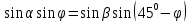
Или
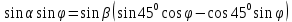
Делим обе части на
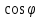 :
: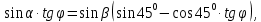
откуда
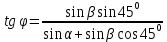
Вычисляем:
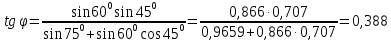
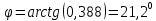
Из второго равенства (1) определяем:
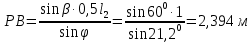
Определяем расстояние
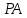 из треугольника
из треугольника 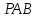 по теореме синусов:
по теореме синусов: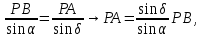
где
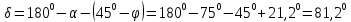
Тогда
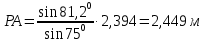
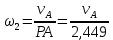
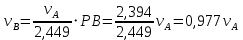
Зависимость между перемещениями такая же, то есть:
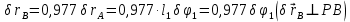
Для нахождения
 воспользуемся тем, что проекции
воспользуемся тем, что проекции  и
и  на прямую
на прямую  должны быть равны друг другу, то есть:
должны быть равны друг другу, то есть: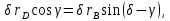
откуда
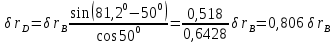
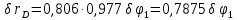
Составляем для механизма уравнение (1):