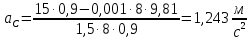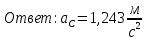Используя найденные значения 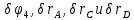, получим: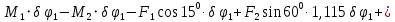





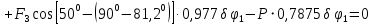
Так как 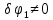, то из этого уравнения следует: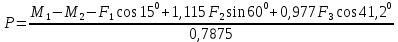







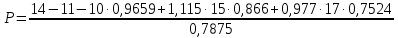
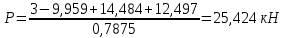
Ответ:

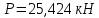
Задание 12
Дано:



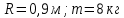
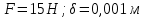
Найти:

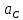
Решение

---

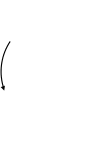
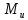
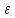
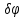
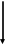
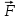
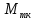
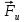
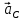
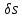
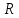
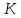
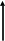
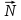
Рис. 1
Рассмотрим движение колеса (рис. 1). Для определения ускорения центра колеса применим общее уравнение динамики: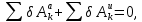

(1)

где 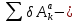сумма элементарных работ активных сил, 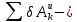сумма элементарных работ сил инерции.

Изобразим на чертеже (рис. 1) активные силы: силу тяжести 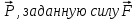и момент пары сил сопротивления качению колеса. Задавшись направлением ускорения 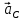, изобразим силу инерции 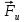и пару сил инерции с моментом , величины которых равны: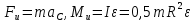



Сообщим системе возможное перемещение 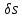и составим уравнение (1).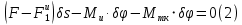



Выразим перемещение

---

через перемещение . Точка является мгновенным центром скоростей колеса, следовательно,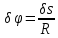



Момент пары сил трения качения колеса равен:



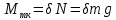
Подставив все величины в уравнение (2), получим:



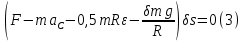
Угловое ускорение выразим через искомое ускорение :



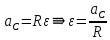
Учитывая, что 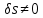, приравняем к нулю выражение, стоящее в (3) в скобках. Тогда получим: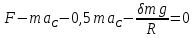



Решая это уравнение относительно , получим: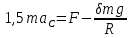





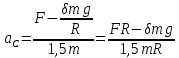
Вычисляем:

---

Смотрите также файлы

• Практическая работа 1 Задание Выберите две теории и сделайте их сопоставительную характеристику, заполнив таблицу.rtf

• Что такое дружба.doc

• Введение Профессия учителя всегда считалась одной из самых почетных, уважаемых и ответственных. Учителя не только осуществляют обучение детей, он воспитывает будущее поколение великой страны..docx

• Кейс дело спелеологов.docx

• Тип государства и его формы.docx