Файл: Задача Скорость прямолинейного движения SS(tt)S(t).docx
Добавлен: 25.10.2023
Просмотров: 102
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
D на плоскости Oxy, было полным дифференциалом, необходимо и достаточно выполнения условия 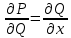 .
.
55. Уравнения Лагранжа и Клеро.
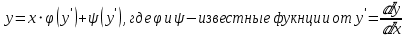 – Уравнение Лагранжа
– Уравнение Лагранжа
Уравнение Клеро -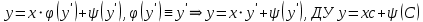
56. Основные понятия. Уравнения, допускающие понижение порядка.
ДУ высших порядков, ДУ 2 порядка, Решение, общее решение, частное решение
Метод понижения порядка: с помощью замены переменной ДУ сводится к уравнению, порядок которого ниже.
Частный случай y’’=f(y’),
y’=p(x), y’’=p’=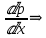 получаем уравнение p’=f(p) с разделяющимися переменными
получаем уравнение p’=f(p) с разделяющимися переменными
… еще есть…
57. Линейные дифференциальные уравнения высших порядков.
Уравнение вида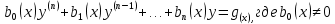
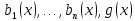 — это заданные функции (от х), называется линейным ДУ n-го порядка
— это заданные функции (от х), называется линейным ДУ n-го порядка
 - свободный член
- свободный член
Разделим уравнение на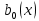
и обозначим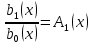 ;…;
;…; 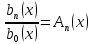 ,
, 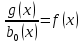
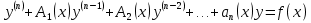
58. Интегрирование линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Пусть дано ЛОДУ 2-го порядка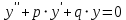 , где p и q – постоянные. Для нахождения общего решения уравнения достаточно найти два его частных решения, образующих фундаментальную систему.
, где p и q – постоянные. Для нахождения общего решения уравнения достаточно найти два его частных решения, образующих фундаментальную систему.
Частное решение в виде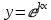 (k- некоторое число). Дифференцируем функцию 2 раза и, подставляя найденные значения, получаем
(k- некоторое число). Дифференцируем функцию 2 раза и, подставляя найденные значения, получаем 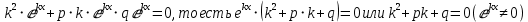 – характеристические уравнения
– характеристические уравнения
При решении характеристических уравнений возможны 3 случая:
Частные решения: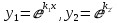
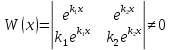 – определитель Вронского
– определитель Вронского
Общее решение: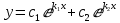
Частное решение: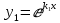
W(x)=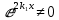
Общее решение: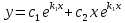
Частное решение: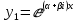 и
и 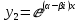
Общее решение: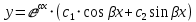
59. Интегрирование линейных однородных дифференциальных уравнений n-го порядка с постоянными коэффициентами.
Задача нахождения общего решения ЛОДУ (n>2) порядка с постоянными коэф.
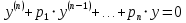 , где
, где 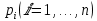 – числа, решается аналогично случаю уравнению 2-го порядка с постоянным коэф.
– числа, решается аналогично случаю уравнению 2-го порядка с постоянным коэф.
Частное решение: , где k- постоянная
, где k- постоянная
Характеристическое уравнение: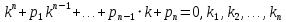 – корни хар-кого уравнения
– корни хар-кого уравнения
Замечание: не все из корней уравнения обязаны быть различными.
Существует 3 случая.
1 случай: все корни уравнения действительны и просты (различны). Общее решение: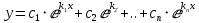
2 случай: все корни действительные, но не все простые (есть корни, имеющие кратность mk>1). Тогда каждому простому корню k соответствует одно частное решение вида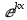 , а каждому корню k кратности mk>1 соответствует m частных решений
, а каждому корню k кратности mk>1 соответствует m частных решений 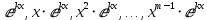
3 случай: среди корней уравнения, есть комплексно-сопряженные. Тогда каждой паре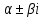 простых комплексно-сопряженных корней, соответствует 2 частных решения:
простых комплексно-сопряженных корней, соответствует 2 частных решения:
Частное решение: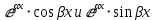 , а каждой паре α±
, а каждой паре α±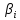 , корней кратности mk>1 соответствуют 2m частных решений вида:
, корней кратности mk>1 соответствуют 2m частных решений вида:
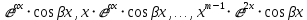 или
или
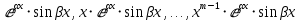
60. Структура общего решения ЛНДУ второго порядка. Метод вариации произвольных постоянных.
y’’+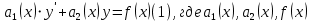 – заданная непрерывная на (a,b) функция. Уравнение
– заданная непрерывная на (a,b) функция. Уравнение 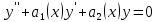 (2), левая часть которого совпадает с левой частью ЛНДУ называется соответствующим ему однородном уравнениям.
(2), левая часть которого совпадает с левой частью ЛНДУ называется соответствующим ему однородном уравнениям.
Теорема: (структура общего решения ЛНДУ).
Общим решением y уравнения (1) является сумма его произвольного частного решения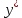
и общего решения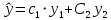 соответствующего однородного уравнения (2), то есть
соответствующего однородного уравнения (2), то есть 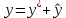
Метод вариации произвольных постоянных:
Частное решение можно найти из
можно найти из 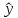 методом вариации произвольных постоянных (метод Лагранжа)
методом вариации произвольных постоянных (метод Лагранжа)
Пусть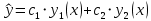 – общее решение уравнения, постоянные
– общее решение уравнения, постоянные 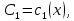
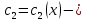 заменяем на неизвестные функции и подбираем их так, чтобы функция
заменяем на неизвестные функции и подбираем их так, чтобы функция 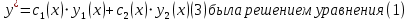
Найдем производную частного решения:
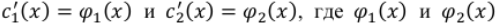 – некоторые функции от x. Интегрируя эти функции, находим
– некоторые функции от x. Интегрируя эти функции, находим 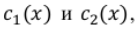 а затем по формуле (3) составляем частное решение уравнения (1).
а затем по формуле (3) составляем частное решение уравнения (1).
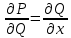 .
.55. Уравнения Лагранжа и Клеро.
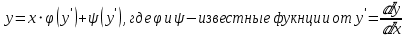 – Уравнение Лагранжа
– Уравнение Лагранжа-
y’=p;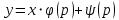
-
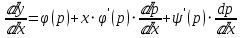 , то есть
, то есть 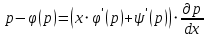
-
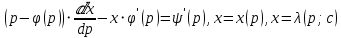
Уравнение Клеро -
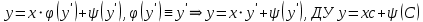
56. Основные понятия. Уравнения, допускающие понижение порядка.
ДУ высших порядков, ДУ 2 порядка, Решение, общее решение, частное решение
Метод понижения порядка: с помощью замены переменной ДУ сводится к уравнению, порядок которого ниже.
-
Пусть дано уравнение: y’’= f(x); введем p(x)=y’, тогда y’’=p’(x) следовательно p’(x)=f(x) сводится к виду y’=p(x) -
Пусть дано уравнение y’’=f(x,y’) не содержащая явно искомой функции y
-
y’=p, где p=p(x) -
y’’=p’ и p’=f(x,p) -
p= (x,
(x, 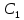 ) – общее решение ДУ 1-го порядка
) – общее решение ДУ 1-го порядка -
p y’; y’=
y’; y’= 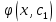
-
Общее решение ДУ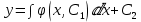
Частный случай y’’=f(y’),
y’=p(x), y’’=p’=
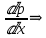 получаем уравнение p’=f(p) с разделяющимися переменными
получаем уравнение p’=f(p) с разделяющимися переменными … еще есть…
57. Линейные дифференциальные уравнения высших порядков.
Уравнение вида
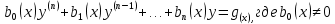
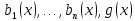 — это заданные функции (от х), называется линейным ДУ n-го порядка
— это заданные функции (от х), называется линейным ДУ n-го порядка - свободный член
- свободный членРазделим уравнение на
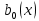
и обозначим
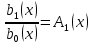 ;…;
;…; 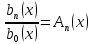 ,
, 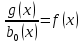
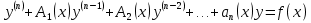
58. Интегрирование линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Пусть дано ЛОДУ 2-го порядка
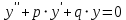 , где p и q – постоянные. Для нахождения общего решения уравнения достаточно найти два его частных решения, образующих фундаментальную систему.
, где p и q – постоянные. Для нахождения общего решения уравнения достаточно найти два его частных решения, образующих фундаментальную систему.Частное решение в виде
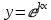 (k- некоторое число). Дифференцируем функцию 2 раза и, подставляя найденные значения, получаем
(k- некоторое число). Дифференцируем функцию 2 раза и, подставляя найденные значения, получаем 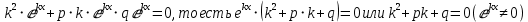 – характеристические уравнения
– характеристические уравненияПри решении характеристических уравнений возможны 3 случая:
-
1 случай: Корни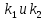 уравнения действительные и различные
уравнения действительные и различные 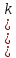 )
)
Частные решения:
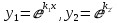
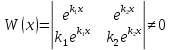 – определитель Вронского
– определитель ВронскогоОбщее решение:
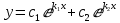
-
2 случай: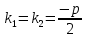 (D=0)
(D=0)
Частное решение:
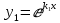
W(x)=
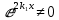
Общее решение:
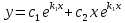
-
3 случай: корни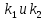 комплексные:
комплексные: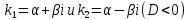
Частное решение:
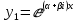 и
и 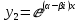
Общее решение:
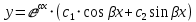
59. Интегрирование линейных однородных дифференциальных уравнений n-го порядка с постоянными коэффициентами.
Задача нахождения общего решения ЛОДУ (n>2) порядка с постоянными коэф.
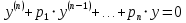 , где
, где 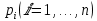 – числа, решается аналогично случаю уравнению 2-го порядка с постоянным коэф.
– числа, решается аналогично случаю уравнению 2-го порядка с постоянным коэф.Частное решение:
 , где k- постоянная
, где k- постоянная Характеристическое уравнение:
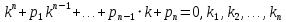 – корни хар-кого уравнения
– корни хар-кого уравнения Замечание: не все из корней уравнения обязаны быть различными.
Существует 3 случая.
1 случай: все корни уравнения действительны и просты (различны). Общее решение:
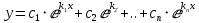
2 случай: все корни действительные, но не все простые (есть корни, имеющие кратность mk>1). Тогда каждому простому корню k соответствует одно частное решение вида
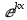 , а каждому корню k кратности mk>1 соответствует m частных решений
, а каждому корню k кратности mk>1 соответствует m частных решений 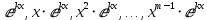
3 случай: среди корней уравнения, есть комплексно-сопряженные. Тогда каждой паре
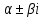 простых комплексно-сопряженных корней, соответствует 2 частных решения:
простых комплексно-сопряженных корней, соответствует 2 частных решения:Частное решение:
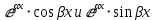 , а каждой паре α±
, а каждой паре α±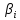 , корней кратности mk>1 соответствуют 2m частных решений вида:
, корней кратности mk>1 соответствуют 2m частных решений вида: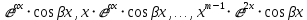 или
или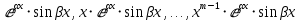
60. Структура общего решения ЛНДУ второго порядка. Метод вариации произвольных постоянных.
y’’+
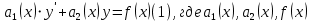 – заданная непрерывная на (a,b) функция. Уравнение
– заданная непрерывная на (a,b) функция. Уравнение 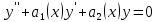 (2), левая часть которого совпадает с левой частью ЛНДУ называется соответствующим ему однородном уравнениям.
(2), левая часть которого совпадает с левой частью ЛНДУ называется соответствующим ему однородном уравнениям.Теорема: (структура общего решения ЛНДУ).
Общим решением y уравнения (1) является сумма его произвольного частного решения
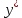
и общего решения
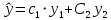 соответствующего однородного уравнения (2), то есть
соответствующего однородного уравнения (2), то есть 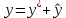
Метод вариации произвольных постоянных:
Частное решение
 можно найти из
можно найти из 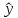 методом вариации произвольных постоянных (метод Лагранжа)
методом вариации произвольных постоянных (метод Лагранжа)Пусть
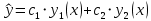 – общее решение уравнения, постоянные
– общее решение уравнения, постоянные 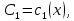
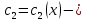 заменяем на неизвестные функции и подбираем их так, чтобы функция
заменяем на неизвестные функции и подбираем их так, чтобы функция 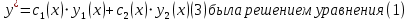
Найдем производную частного решения:
-
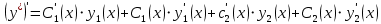
-
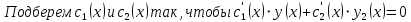 (4)
(4) -
Тогда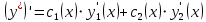
-
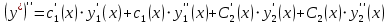
-
Подставляем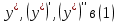
-
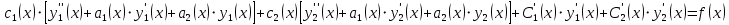
-
Т.к.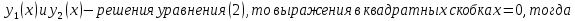
-
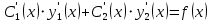 (5)
(5) -
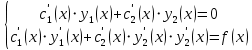 (6)
(6) -
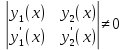 т.к это определитель Вронского для фундаментальной системы частных решений
т.к это определитель Вронского для фундаментальной системы частных решений 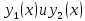 уравнения (2). Поэтому система (6) имеет единственное решение:
уравнения (2). Поэтому система (6) имеет единственное решение: