Файл: Задача Скорость прямолинейного движения SS(tt)S(t).docx
Добавлен: 25.10.2023
Просмотров: 97
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Производная функции. Задачи, приводящие к понятию производной.
Задача 1. Скорость прямолинейного движения
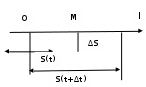
∆S=S(t+∆t)-S(t)
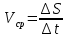
S=S(t) – закон движения точки
Предел средней скорости движения при стремлении к 0 промежутка времени ∆t, называется скорость движения точки в данной момент времени или мгновенной скоростью.
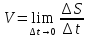 или
или 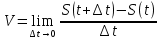
Задача 2. Касательная к криво й
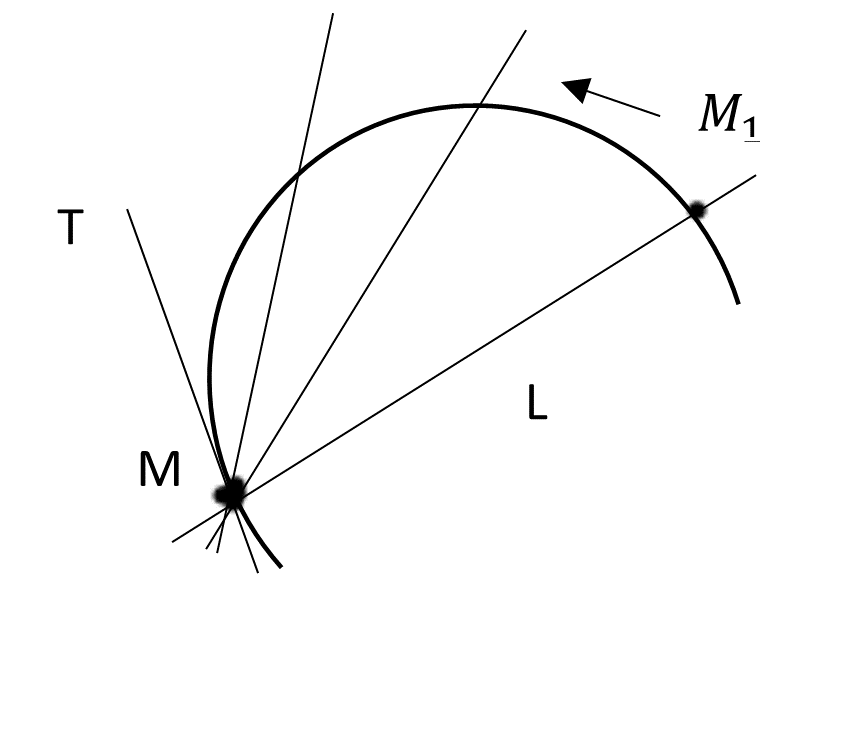 (M;
(M; 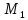 ) -секущая
) -секущая 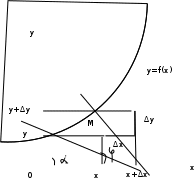 | 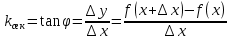 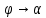 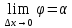 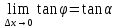 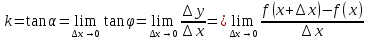 – угловой коэффициент касательной – угловой коэффициент касательной |
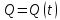
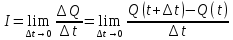
V=S`t;
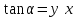 ; I=Q`t
; I=Q`t2. Определение производной, ее механический и геометрический смысл.
Пусть функция y=f(x) определена на некотором интервале (а;b)
-
x є (a;b); x+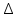 xє(a;b)
xє(a;b) -
∆y = f(x+∆x) – f(x) -
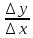
-
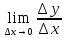 – этот предел (если он существует) называют производной функцией f(x)
– этот предел (если он существует) называют производной функцией f(x)
Обозначение производной:
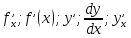
Производной функцией y=f(x) в точке
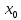 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. 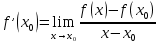
Функция y=f(x), имеющая производную в каждой точке интервала (a;b), называется дифференцируемой в этом интервале. Операция нахождения производной функции называется дифференцированием.
Механический смысл производной:скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t (v=S`t) .
Физический смысл производной: если функция y=f(x) описывает какой-либо физический процесс, то производная y` есть скорость протекания этого процесса.
Геометрический смысл производной: производная
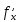 в точке x равна угловому коэффициенту касательной графику функции y=f(x) в точке, абсцисса которой равна x.
в точке x равна угловому коэффициенту касательной графику функции y=f(x) в точке, абсцисса которой равна x.3. Уравнение касательной и нормали к кривой.
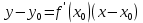 – уравнение касательной
– уравнение касательнойПрямая, перпендикулярная касательной в точке касания, называется нормалью кривой.
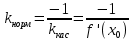
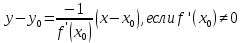 -уравнение нормали
-уравнение нормали4. Связь между непрерывностью и дифференцируемостью функции.
Теорема: если функция дифференцируема в некоторой точке, то она непрерывна в ней, но обратная теорема не верна; непрерывная функция может не иметь производной.
Замечание:
-
Существуют односторонние пределы функции y=|x| в точке x=0: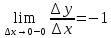 ;
;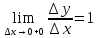 – функция имеет односторонние производные
– функция имеет односторонние производные
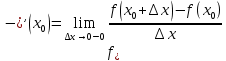 – левая производная функция f в т.
– левая производная функция f в т. 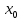
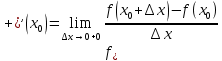 – правая производная функция f в т.
– правая производная функция f в т.

Если
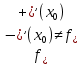 , то производная в точке не существует
, то производная в точке не существуетПроизводной не существует в точке разрыва.
-
Производная y’=f’(x) непрерывной функции y=f’(x) сама необязательно является непрерывной.
Если функция y=f(x) имеет непрерывную производную y’=f’(x) в некотором интервале (a;b), то функция называется гладкой
5. Производная суммы, разности, произведения и частного функций. Производная сложной и обратной функции.
-
Производная суммы, разности, произведения и частного функций
Пусть функции u=u(x) и v=v(x) – две дифференцируемые функции в интервале (a;b).
Теорема: производная суммы (разности) двух функций равна сумме (разности) производных этих функций
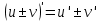
Теорема о производной: производная произведения двух функций равна произведению производной первого сомножителя на второй + произведение первого сомножителя на производную второго.
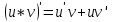
Следствие 1: (C*u)’ = C*u’, C=const
Следствие 2: (u*v*w)’=u’vw+uv’w+uvw’
Теорема: производная частного двух функций
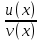 , если v(x)≠0 равна дроби, числитель которой есть разность произведений знаменателя дроби v на производную числителя и числителя дроби u на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
, если v(x)≠0 равна дроби, числитель которой есть разность произведений знаменателя дроби v на производную числителя и числителя дроби u на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя. 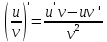 , v≠0
, v≠0Следствие 1:
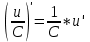 , C=const
, C=constСледствие 2:
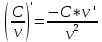 , C=const
, C=const-
Производная сложной и обратной функции.
Пусть y=f(u) и u=
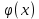 , тогда
, тогда 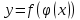 – сложная функция с промежуточным аргументом и независимым аргументом x.
– сложная функция с промежуточным аргументом и независимым аргументом x.Теорема: если функция
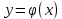 имеет производную u`(x) в точке х, а функция y=f(u) имеет производную y`(u) в соответствующей точке
имеет производную u`(x) в точке х, а функция y=f(u) имеет производную y`(u) в соответствующей точке
 , то сложная функция
, то сложная функция  имеет производную y`(x) в точке х, которая находится по формуле: y`(x)=y`(u)*u`(x)
имеет производную y`(x) в точке х, которая находится по формуле: y`(x)=y`(u)*u`(x)Если промежуточных аргументов несколько: y=f(u), u=
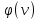 , v=g(x), то y`(x)=y`(u)*u`(v)*v`(x)
, v=g(x), то y`(x)=y`(u)*u`(v)*v`(x)y=f(u(
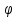 (v(x))))
(v(x))))Производная обратной функции
Пусть y=f(x) и x=
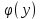 – взаимно обратные функции
– взаимно обратные функцииТеорема: если функция y=f(x) строго монотонна на интервале (a;b) и имеет не равную 0 производную f `(x) в произвольной точке этого интервала, то обратная ей функция x=
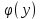 также имеет производную
также имеет производную 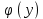 в соответствующей точке, определенную равенством:
в соответствующей точке, определенную равенством: 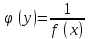 или
или 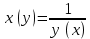
Производная обратной функции равна обратной величине производной данной функции.
Правило дифференцирования обратной функции:
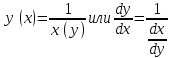
6. Производные основных элементарных функций. Гиперболические функции и их производные.
-
Производные основных элементарных функций
-
Степенная функция: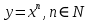
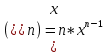
-
Показательная функция: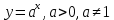
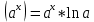
-
Логарифмическая функция: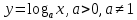
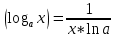
-
Тригонометрические функции: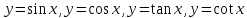
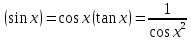
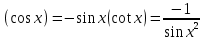
-
Обратные тригонометрические функции
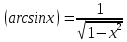
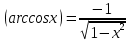
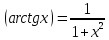
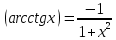
-
Гиперболические функции и их производные
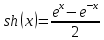 – гиперболический синус
– гиперболический синус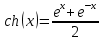 -гиперболический косинус
-гиперболический косинус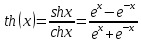 – гиперболический тангенс
– гиперболический тангенс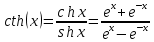 – гиперболический котангенс
– гиперболический котангенс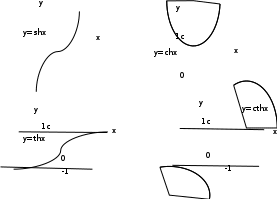
7. Правила дифференцирования и основные формулы дифференцирования. Таблица производных.
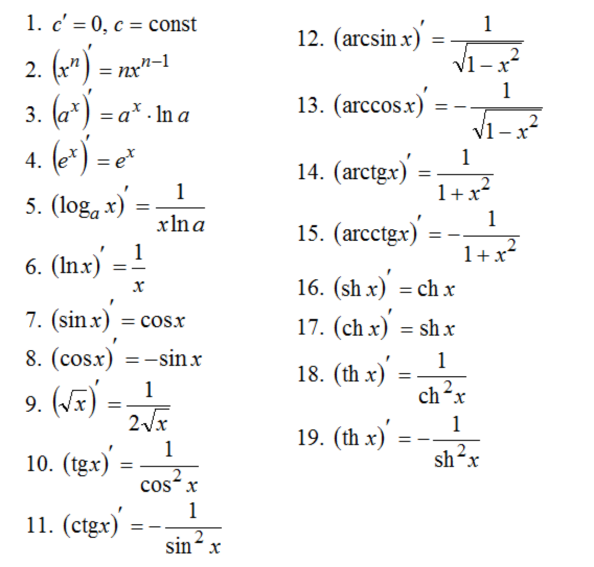 См. вопрос 5
См. вопрос 58. Логарифмическое дифференцирование.
В ряде случаев для нахождения производной целесообразно функцию сначала прологарифмировать, а затем результат продифференцировать. Данную операцию называют логарифмическим дифференцированием.
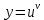 -степенно-показательная функция
-степенно-показательная функция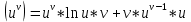
9. Неявно заданная функция. Функция, заданная параметрически.
-
Неявно заданная функция.
Если функция задана уравнением y=f(x), разрешенным относительно y, то функция задана в явном виде.
Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, неразрешенного относительно y.
Явная функция переходит в неявную. Неявная функция не переходит в явную
Пример неявной функции: y+2x+cosy-1=0;