Файл: Задача Скорость прямолинейного движения SS(tt)S(t).docx
Добавлен: 25.10.2023
Просмотров: 98
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Теорема (необходимый признак сходимости): Если ряд
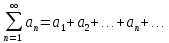 сходится, то его общий член
сходится, то его общий член 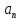 стремится к нулю, т.е.
стремится к нулю, т.е. 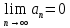
Следствие (достаточное условие расходимости ряда): Если
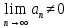 или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится.39. Гармонический ряд. Обобщенный гармонический ряд.
-
Гармонический ряд
 (5)
(5)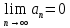
Однако ряд (5) расходится
-
Обобщенный гармонический ряд.
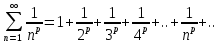 , где p>0 – действительное число. (p>1 - сходится, иначе расх)
, где p>0 – действительное число. (p>1 - сходится, иначе расх)40. Признаки сравнения рядов. Признак Даламбера.
-
Признаки сравнения рядов
Теорема: пусть даны два знакоположительных ряда.
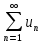 (6) и
(6) и 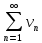 (7)
(7)Если для всех n выполняется неравенство un
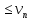 , то из сходимости ряда (7) следует сходимость ряда (6), из расходимости ряда (6) следует расходимость ряда (7).
, то из сходимости ряда (7) следует сходимость ряда (6), из расходимости ряда (6) следует расходимость ряда (7).Теорема (предельный признак сравнения): пусть даны два знакоположительных ряда (6) и (7).
Если существует конечный, отличный от 0 предел
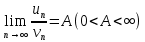 , то ряды (6) и (7) сходятся и расходятся одновременно.
, то ряды (6) и (7) сходятся и расходятся одновременно.-
Признак Даламбера
Пусть дан ряд
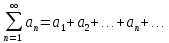 (1) с положительными членами и существует конечный или бесконечный предел
(1) с положительными членами и существует конечный или бесконечный предел 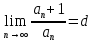 . Тогда ряд сходится при d<1 и расходится при d>1
. Тогда ряд сходится при d<1 и расходится при d>1Замечания
-
Если d=1, то ряд (1) может быть как сходящимся, так и расходящимся -
Признак Даламбера целесообразно применять, когда общий член ряда содержит выражение вида n! или un
41. Радикальный признак Коши. Интегральный признак Коши.
-
Радикальный признак Коши.
Пусть дан ряд (1) с положительными членами и существует конечный и бесконечный предел
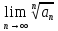 =k. Тогда ряд сходится при k<1 и расходится при k>1.
=k. Тогда ряд сходится при k<1 и расходится при k>1.-
Интегральный признак Коши.
Если члены знакоположительного ряда
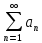 могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке [1; +
могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке [1; + ) функции
) функции  так что a1=
так что a1=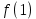 , а2=
, а2=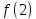 …, аn=
…, аn=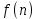 ,…, то:
,…, то:-
Если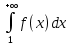 сходится, то сходится и ряд (1)
сходится, то сходится и ряд (1) -
Если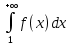 расходится, то расходится также ряд (1)
расходится, то расходится также ряд (1)
Замечания:
Вместо интеграла
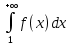 можно брать интеграл
можно брать интеграл 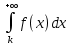 , где
, где 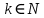 , k>1
, k>142. Знакочередующиеся ряды. Признак Лейбница.
Знакочередующимся рядом называется ряд вида U1-U2+U3-U4+…+
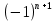 Un+…+= =
Un+…+= =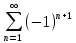 Un, где Un>0,
Un, где Un>0, 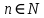 (1)
(1)Теорема (Достаточный признак сходимости. Признак Лейбница)
Знакочередующийся ряд сходится если:
-
Условие: Последовательность абсолютных величин членов ряда монотонно убывает U1>U2>U3>…>Un>…; -
Условие: Общий член ряда стремится к 0.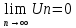 . При этом сумма ряда удовлетворяет неравенствам 0
. При этом сумма ряда удовлетворяет неравенствам 0
Замечания
-
Исследование знакочередующегося ряда вида -U1+U2-U3+U4-… сводится путем умножения всех его членов на -1 к исследованию ряда (1). Ряды, для которых выполняется условие теоремы Лейбница называются рядами Лейбница. -
Соотношение 0
43. Общий достаточный признак сходимости знакопеременных рядов. Свойства абсолютно сходящихся рядов.
-
Общий достаточный признак сходимости знакопеременных рядов.
Числовой ряд
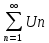 , содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.
, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.Теорема (общий достаточный признак сходимости):
Пусть дан знакопеременный ряд U1+U2+…+Un+…. Если сходится ряд |U1|+|U2|+…+|Un|+…, составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд. Обратное утверждение не справедливо!
-
Свойства абсолютно сходящихся рядов.
Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.
Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Основные св-ва абс:
-
Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится, и имеет ту же сумму S, что и исходный ряд (относится к теореме Дирихле) -
Абсолютно сходящиеся ряды с суммами S1 и S2 можно почленно складывать (вычитать). В результате получится абсолютно сходящийся ряд, сумма которого равна S1+S2 (S1-S2) -
Под произведением двух рядов u1+u2+… и v1+v2+… понимают ряд вида
(U1V1)+(U1V2+U2V1)+(U1V3+U2V2+U3V1)+…+(U1Vn+U2Vn-1+…+UnV1)+… . Произведение двух абсолютно сходящихся рядов с суммами S1 и S2 есть абсолютно сходящийся ряд, сумма которого равна S1*S2
Действия над знакопеременными рядами нельзя производить, не убедившись в их абсолютной сходимости.
44. Абсолютная и условная сходимости числовых рядов.
-
Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. -
Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Основные свойства
-
Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный, из него перестановкой членов, также сходится, и имеет туже сумм S, что и исходный ряд (относится к теореме Дрихле) -
Абсолютно сходящиеся ряды с суммами S1 и S2 можно почленно складывать (вычитать). В результате получится абсолютно сходящийся ряд, сумма которого равна S1+S2 (S1-S2) -
Под произведением двух рядов u1+u2+… и v1+v2+… понимают ряд вида
(U1V1)+(U1V2+U2V1)+(U1V3+U2V2+U3V1)+…+(U1Vn+U2Vn-1+…+UnV1)+… . Произведение двух абсолютно сходящихся рядов с суммами S1 и S2 есть абсолютно сходящийся ряд, сумма которого равна S1*S2
Действия над знакопеременными рядами нельзя производить, не убедившись в их абсолютной сходимости.
45. Основные понятия для функционального ряда. Сходимость степенных рядов. Теорема Н. Абеля.
Функциональные ряды:
-
Ряд, членами которого является функция от х, называется функциональным:
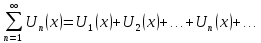
-
Придавая х определенное значение , мы получим числовой ряд
, мы получим числовой ряд 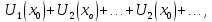 может быть как сходящимся, так и расходящимся
может быть как сходящимся, так и расходящимся -
Если полученный числовой ряд сходится, то точка называется точкой сходимости ряда, если же ряд расходится – точка расходимости функционального ряда.
называется точкой сходимости ряда, если же ряд расходится – точка расходимости функционального ряда. -
Совокупность числовых значений аргумента xпри которых функциональный ряд сходится, называется его областью сходимости. -
В области сходимости функционального ряда, его сумма является некоторой функцией от х, то есть S=S(x). Определяется в области сходимости равенством:
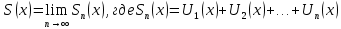
-
Степенной ряд – это ряд, членами которого является степенные функции аргумента x
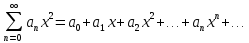
-
Действительные (или комплексные) числа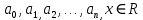 , называются коэффициентами ряда
, называются коэффициентами ряда -
Степенной ряд, разложенный (расположенный) по степеням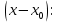
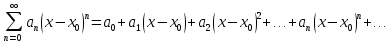
-
Область сходимости степенного ряда содержит, по крайне мере, одну точку x=0
Теорема Абеля:
Если степенной ряд сходится при
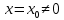 , то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству
, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству
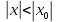
Следствие: Если ряд расходится при
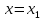 , то он расходится и при всех Х, удовлетворяющих неравенству
, то он расходится и при всех Х, удовлетворяющих неравенству 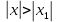
46. Интервал и радиус сходимости степенного ряда. Свойства степенных рядов.
-
Интервал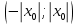 , называется интервал сходимости степенного ряда. Пусть
, называется интервал сходимости степенного ряда. Пусть 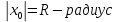 сходимости степенного ряда.
сходимости степенного ряда. 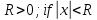 , то ряд абсолютно сходится,
, то ряд абсолютно сходится, 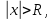 то ряд расходится
то ряд расходится -
Радиус абсолютной сходимости: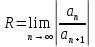 -(Признак Даламбера)
-(Признак Даламбера) -
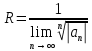 – (радикальный признак Коши)
– (радикальный признак Коши)
Замечание:
-
Если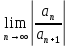 =0, то ряд абсолютно сходится на всей числовой оси
=0, то ряд абсолютно сходится на всей числовой оси 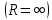 .
.
Если
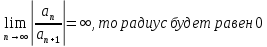
-
Интервал сходимости степенного ряда, разложенного по степеням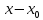 , находят из неравенства
, находят из неравенства 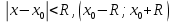 – интервал сходимости
– интервал сходимости -
Если степенной ряд содержит не все степени х, то есть задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости, а непосредственно применяя признак Даламбера или Коши для ряда, составленного из модулей членов данного ряда.
Основные свойства степенных рядов:
1) Сумма S(x) степенного ряда является непрерывной функцией в интервале сходимости от
(-R;R)
2) Степенные ряды
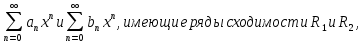 можно почленно складывать, вычитать и умножать.
можно почленно складывать, вычитать и умножать.3) Степенной ряд, внутри интервала сходимости, можно почленно дифференц., при этом для ряда