Файл: Задача Скорость прямолинейного движения SS(tt)S(t).docx
Добавлен: 25.10.2023
Просмотров: 99
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-x+y=0
Если неявная функция задана уравнением F(x;y)=0, достаточно продифференцировать уравнение по х, рассматривая при этом у как функцию х.
Пусть зависимость между аргументом х и функцией у задана параметрически в виде уравнений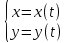
, где t – вспомогательная переменная, называемая параметром.
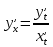
10. Производные высших порядков явно заданной функции. Механический смысл производной второго порядка.
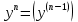
Вторая производная от пути времени, есть величина ускорения прямолинейного движения точки S``(t)=a
11. Производные высших порядков неявно заданной функции.
Продифференцировав по х первую производную, получим вторую производную от неявной функции. В не войдут х, у и у`. Подставляя найденное значение у` в выражение второй производной, выразим y`` через х и у.
Аналогично поступаем для нахождения производной n-ого порядка.
12. Производные высших порядков от функций, заданных параметрически.
; 
; 
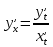
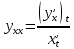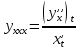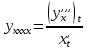
13. Понятие и геометрический смысл дифференциала функции. Основные теоремы о дифференциалах.
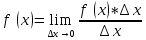- главная часть приращения функции ∆у(числитель предела)
Дифференциалом функции y=f (x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента и обозначается dy ( или df(x)); dy=f `(x)*∆x.
Дифференциал dy называют также дифференциалом 1-ого порядка dy=f `(x)dx.
Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Геометрический смысл дифференциала функции.
Дифференциал функции y=f (x) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.
Основные теоремы о дифференциалах:
dy(const)=0 dy=0*dx
d*(u+v) = du + dv
d(u*v) = v*du+u*du
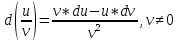
14. Применение дифференциала к приближенным вычислениям. Дифференциалы высших порядков.
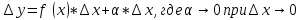
Или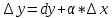
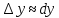
– это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
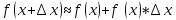
Дифференциал от дифференциала функции y=f (x) называется ее вторым дифференциалом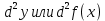
.
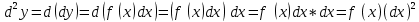
Дифференциал n-ого порядка есть дифференциал от дифференциала (n-1)-ого порядка:
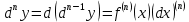
Рассматриваемые выше формулы справедливы, если х – независимая переменная.
15. Формула Тейлора для многочлена. Формула Тейлора для произвольной функции
Пусть функция f(x) есть многочлен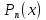
в степени n.
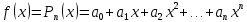
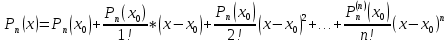
Т
еорема: если функция f (x) определена в некоторой окрестности точки 
и имеет в ней производные до (n+1)-ого порядка (включительно), то для любого х из этой окрестности найдется точка С, принадлежащая интервалу Сє( ;х) такая, что справедлива формула:
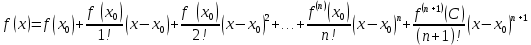
(C= +Ѳ(x- )), 0<Ѳ<1
Сокращенная формула: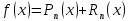
При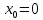
получаем частный случай формулы Тейлора – формулу Макларена:
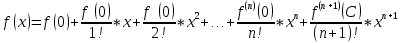(C=Ѳx, 0<Ѳ<1)
16. Основные теоремы о дифференцируемых функциях. Правило Лопиталя.
Теорема 1 (Ролль): Если функция f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и на концах отрезка принимает одинаковые значения f(a)=f(b), то найдётся хотя бы одна точка Сϵ(a; b), в которой производная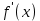
обращается в 0, т.е.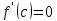 
Теорема 2 (Коши): Если ф-и f(x) и
(x) непрерывны на отрезке [a;b], дифференцируемы на интервале (a;b) причём 
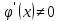для Xϵ(a; b), то найдётся хотя бы одна точка Сϵ(a; b) такая, что выполняется равенство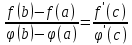 
Теорема 3 (Лагранж): Если функция f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), то найдётся хотя бы одна точка Сϵ(a; b) такая, что выполняется равенство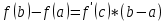
- формула Лагранжа (формула о конечном приращении).
Следствие 1: Если производная функции равна 0 на некотором промежутке, то функция постоянна на этом промежутке.
Следствие 2: Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
Правило Лопиталя:
Теорема 1 (Правило Лопиталя, раскрытие неопределённости вида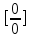
).
Пусть ф-и f(x) и (x) непрерывны на отрезке [a;b], дифференцируемы в окрестности точки x0 и обращаются в 0 в этой точке (f(x0)= (x0)=0). Пусть 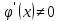в окрестности т. x0. Если существует предел 
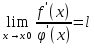, то
.
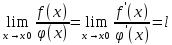Теорема 2 (Правило Лопиталя, раскрытие неопределённости вида [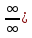
Пусть ф-и f(x) и
Если неявная функция задана уравнением F(x;y)=0, достаточно продифференцировать уравнение по х, рассматривая при этом у как функцию х.
-
Функция, заданная параметрически.
Пусть зависимость между аргументом х и функцией у задана параметрически в виде уравнений
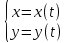, где t – вспомогательная переменная, называемая параметром.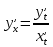 10. Производные высших порядков явно заданной функции. Механический смысл производной второго порядка.
-
Производные высших порядков явно заданной функции.
-
Производная y`=f `(x) функции y=f (x) называется производная 1-ого порядка -
Если функция f `(x) дифференцируема, то ее производная называется производной 2-ого порядка. y``; f ``(x);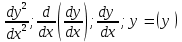
-
Производной n-ого порядка называется производная от производной (n-1)-ого порядка
-
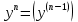
Производные порядка выше первого называются производными высших порядков. Обозначаются: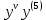
-
Механический смысл производной второго порядка.
Вторая производная от пути времени, есть величина ускорения прямолинейного движения точки S``(t)=a
11. Производные высших порядков неявно заданной функции.
Продифференцировав по х первую производную, получим вторую производную от неявной функции. В не войдут х, у и у`. Подставляя найденное значение у` в выражение второй производной, выразим y`` через х и у.
Аналогично поступаем для нахождения производной n-ого порядка.
12. Производные высших порядков от функций, заданных параметрически.
; ;
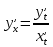
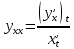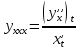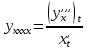
13. Понятие и геометрический смысл дифференциала функции. Основные теоремы о дифференциалах.
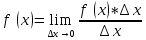- главная часть приращения функции ∆у(числитель предела)Дифференциалом функции y=f (x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента и обозначается dy ( или df(x)); dy=f `(x)*∆x.
Дифференциал dy называют также дифференциалом 1-ого порядка dy=f `(x)dx.
Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Геометрический смысл дифференциала функции.
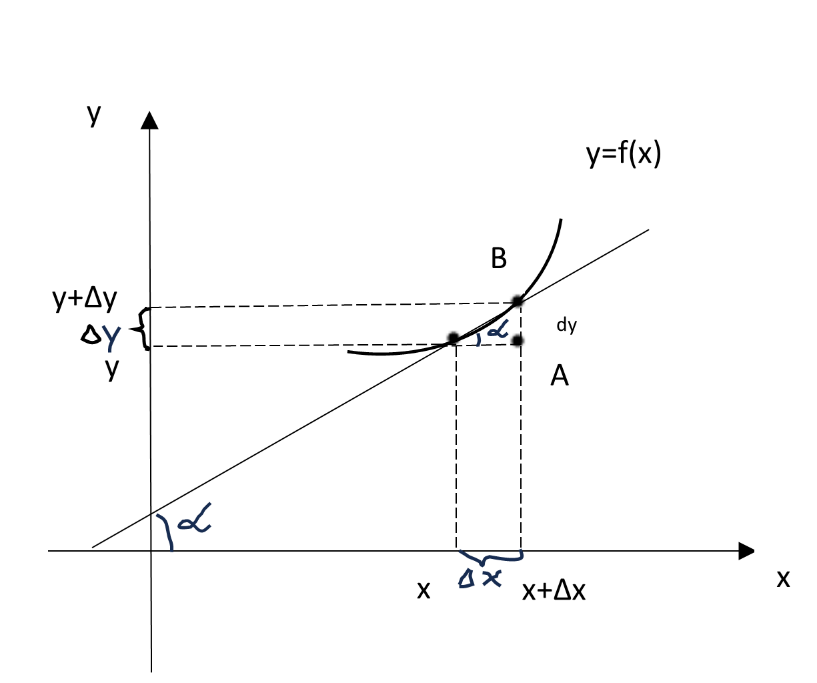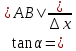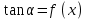 |    AB=f `(x)*∆x dy=AB – длина |
Дифференциал функции y=f (x) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.
Основные теоремы о дифференциалах:
dy(const)=0 dy=0*dx
-
Дифференциал суммы, произведения и частого двух дифференциальных функций определяется следующими формулами:
d*(u+v) = du + dv
d(u*v) = v*du+u*du
-
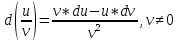
Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента dy=y`(u)*du. -
Инвариантность (неизменность) формулы первого дифференциала заключается в том, что независимо, является ли ее аргумент независимой переменной или является функцией другого аргумента.
14. Применение дифференциала к приближенным вычислениям. Дифференциалы высших порядков.
-
Применение дифференциала к приближенным вычислениям.
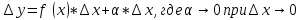
Или
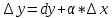
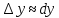
– это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
-
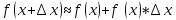
Дифференциалы высших порядков.
Дифференциал от дифференциала функции y=f (x) называется ее вторым дифференциалом
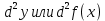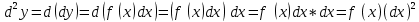
. Дифференциал n-ого порядка есть дифференциал от дифференциала (n-1)-ого порядка:
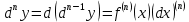
Рассматриваемые выше формулы справедливы, если х – независимая переменная.
15. Формула Тейлора для многочлена. Формула Тейлора для произвольной функции
-
Формула Тейлора для многочлена
Пусть функция f(x) есть многочлен
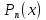в степени n. -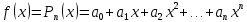
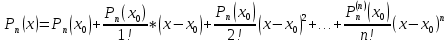
Формула Тейлора для произвольной функции
Т
еорема: если функция f (x) определена в некоторой окрестности точки и имеет в ней производные до (n+1)-ого порядка (включительно), то для любого х из этой окрестности найдется точка С, принадлежащая интервалу Сє( ;х) такая, что справедлива формула: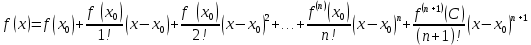 (C=
+Ѳ(x- )), 0<Ѳ<1Сокращенная формула:
-
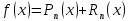
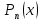– многочлен Тейлора ; -
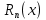– остаточный член формулы Тейлора, записанный в форме Лагранджа.
При
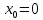получаем частный случай формулы Тейлора – формулу Макларена: 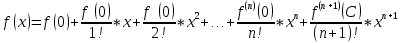(C=Ѳx, 0<Ѳ<1)16. Основные теоремы о дифференцируемых функциях. Правило Лопиталя.
Теорема 1 (Ролль): Если функция f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и на концах отрезка принимает одинаковые значения f(a)=f(b), то найдётся хотя бы одна точка Сϵ(a; b), в которой производная
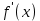обращается в 0, т.е.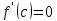 Теорема 2 (Коши): Если ф-и f(x) и
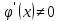(x) непрерывны на отрезке [a;b], дифференцируемы на интервале (a;b) причём для Xϵ(a; b), то найдётся хотя бы одна точка Сϵ(a; b) такая, что выполняется равенство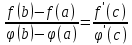 Теорема 3 (Лагранж): Если функция f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), то найдётся хотя бы одна точка Сϵ(a; b) такая, что выполняется равенство
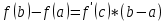- формула Лагранжа (формула о конечном приращении).Следствие 1: Если производная функции равна 0 на некотором промежутке, то функция постоянна на этом промежутке.
Следствие 2: Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
Правило Лопиталя:
Теорема 1 (Правило Лопиталя, раскрытие неопределённости вида
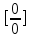).Пусть ф-и f(x) и
(x) непрерывны на отрезке [a;b], дифференцируемы в окрестности точки x0 и обращаются в 0 в этой точке (f(x0)= (x0)=0). Пусть 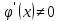в окрестности т. x0. Если существует предел 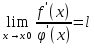, то 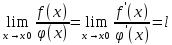.Теорема 2 (Правило Лопиталя, раскрытие неопределённости вида [
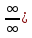
Пусть ф-и f(x) и