Файл: 1. основные результаты и направления развития гидроаэромеханики буровых процессов.doc

Для возникновения течения необходимо выполнение условия

(36)

Объемный расход определяется из уравнения

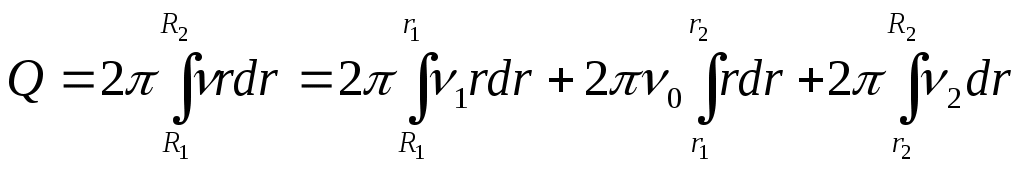(37)

После интегрирования и преобразований, получим

. (38)

Решение полученного уравнения возможно в совокупности с выражениями, позволяющими установить значения констант r₁ и r₂:

(39)

. (40)

Точное решение уравнений (38) – (40) возможно только численными методами с применением компьютера. Такое решение было получено Фредриксоном и Бердом, ими же построены графики для определения радиусов r₁ и r₂, скорости движения “твердого” ядра и расхода Q при известном градиенте давления P, либо наоборот, Р при известном расходе.

В связи со сложностью приведенных выше уравнений были предложены многочисленные упрощения.

Для практических расчетов можно воспользоваться известной зависимостью Дарси-Вейсбаха для градиента давления:

, [Па/м] (41)

Умножив градиента давления Р на длину канала, можно получить давление р в Па.

Для определения коэффициента гидравлического сопротивления используют различные зависимости, например (35), подставляя вместо Re обобщенный параметр Re’:

. (42)

При малых (менее 1200) значениях Re’ для расчета применяют также формулу Е.М. Соловьева

. (43)

Р.И. Шищенко для случая промывки скважины глинистым раствором предложил зависимость, справедливую в диапазоне Re’=1200

---

10000:

. (44)

ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ

1). Переход от ламинарного к турбулентному течению.

Экспериментально доказано, что в трубах при Re<2100 существует только ламинарное течение. При Re>4000 течение, как правило, турбулентное. Между этими значениями – переходная зона.

Для практических расчетов (для ньютоновских жидкостей) принимают Re_кр=2100 или, по другим данным, 2320 (Есьман). Критическая скорость

(1)

Для вязкопластичных жидкостей течение характеризуется двумя параметрами: Re и , поэтому должны выполняться 2 условия:

; , (2)

откуда , (3)

или , (4)

где He – параметр Хедстрема.

---

Критическая скорость

(5)

или (6)

где .

Опытным путем установлено, что c=22,4, по данным других исследователей с=25 или 23,4.

Для определения Re_кр чаще всего используется формула Е.М. Соловьева

, (7)

справедливая в диапазоне .

При анализе течения в кольцевом канале диаметр d заменяется на эквивалентный .

2). Собственно турбулентное течение.

Характеризуется флуктуацией скоростей частиц по всем направлениям. Появляются вихри в результате отрыва пограничного ламинарного слоя. Возникают дополнительные, более высокие напряжения сдвига.

Вывести зависимость между расходом Q и давлением P не удается даже для ньютоновских жидкостей, поэтому используются полуэмпирические теории турбулентности.

Л. Прандтль ввел понятие так называемой динамической скорости:

, (8)

где x – постоянный коэффициент, не зависящий от свойств жидкости;

y – расстояние от стенки трубы.

Проинтегрировав (8) и используя данные опытов И. Никурадзе, Прандтль получил расчетные формулы для профиля скоростей и коэффициента гидравлического сопротивления:

, (9)

(10)

k– эквивалентная шероховатость труб, м (0,02-0,04мм для новых труб).

Формула (9) предназначена для области гладкого трения (гладкие трубы), (10) – для области квадратичного трения (вполне шероховатые трубы). Гидравлически гладкими трубы считают в том случае, когда ламинарный подслой, прилегающий к стенке канала, имеет толщину больше, чем шероховатость стенки.

---

Для шероховатых труб чаще используется формула Колбрука-Уайта
(11)

А.Д. Альтшуль получил широко распространенную ныне формулу:

(12)

При движении ньютоновских жидкостей в гладких трубах применяют также эмпирическую зависимость Блазиуса (1913г.):

(13)

Она дает удовлетворительные результаты при Re=2500÷70000.

При течении вязкопластичных жидкостей наибольшее распространение получила формула Шищенко:

, (14)

где – обобщенный параметр Рейнольдса . Она справедлива при =2500÷50000.

При >50000 значение λ обычно принимают постоянным, равным 0,02.

С учетом сказанного выше, градиент давления

, Па/м (15)

а полное давление

, Па. (16)

ПОТЕРИ ДАВЛЕНИЯ НА МЕСТНЫХ СОПРОТИВЛЕНИЯХ

Местные сопротивления появляются из-за изменения проходного сечения (сужение и расширение канала) и направления потока, т.е. они приурочены к соединениям БТ, промывочным каналам коронок и долот, гидромониторным насадкам долот, переходникам и т.п. В таких элементах происходит завихрение потока, отрыв пограничного слоя, сжатие и расширение потока.

Расчет потерь давления выполняют по формуле Вейсбаха:

, (1)

где ξ – коэффициент местного сопротивления; v – средняя скорость (как правило, за зоной возмущения); ρ – плотность среды.

Коэффициент ξ зависит от конфигурации зоны возмущения

---

, режима течения, реологических свойств среды и шероховатости.

Наиболее известен анализ коэффициента ξ Борда и Карно для резкого изменения площади проходного сечения.

Для резкого сужения канала ими предложена формула

, (2)

где ξ₁– коэффициент на входе; ξ₂– коэффициент на выходе; D – диаметр канала; d – минимальный диаметр в сужении.

В действительности утолщения бурильных труб сглажены и фактические потери давления в этих зонах ниже вычисленных по (2).

Если сравнить сужение проходного сечения в замковом соединении с конфузором, за которым следует диффузор, то можно использовать следующие полуэмпирические соотношения

Для конфузор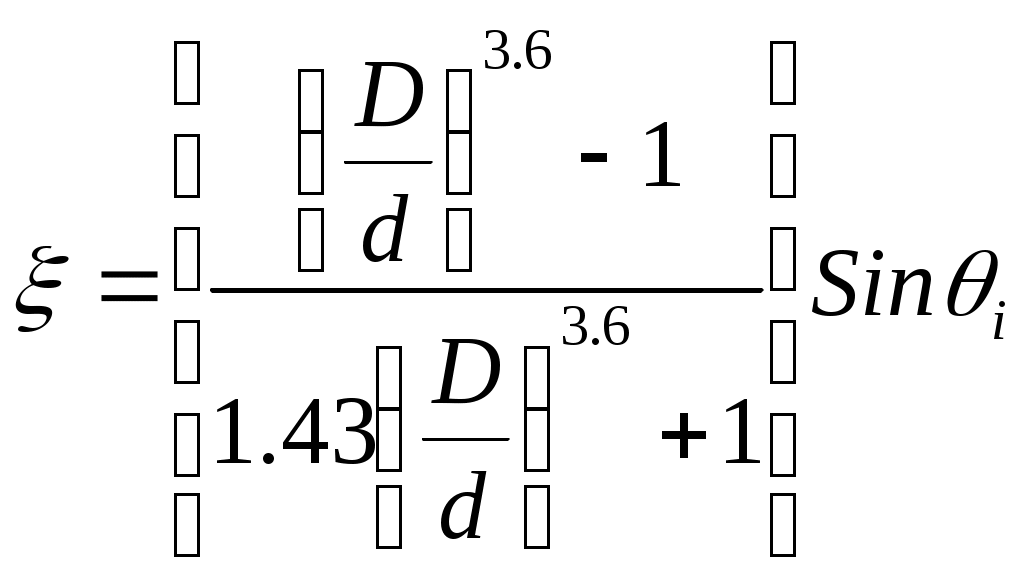а

(а)

для диффузора

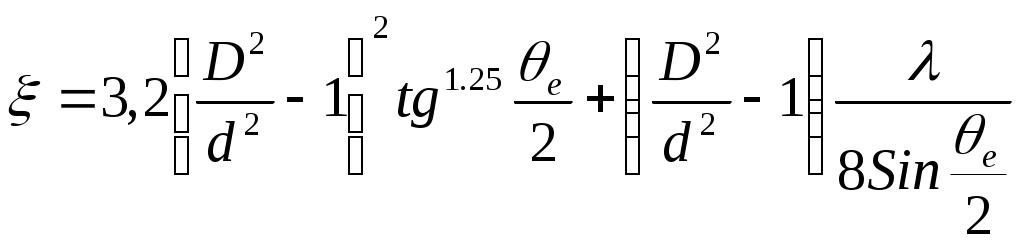(б)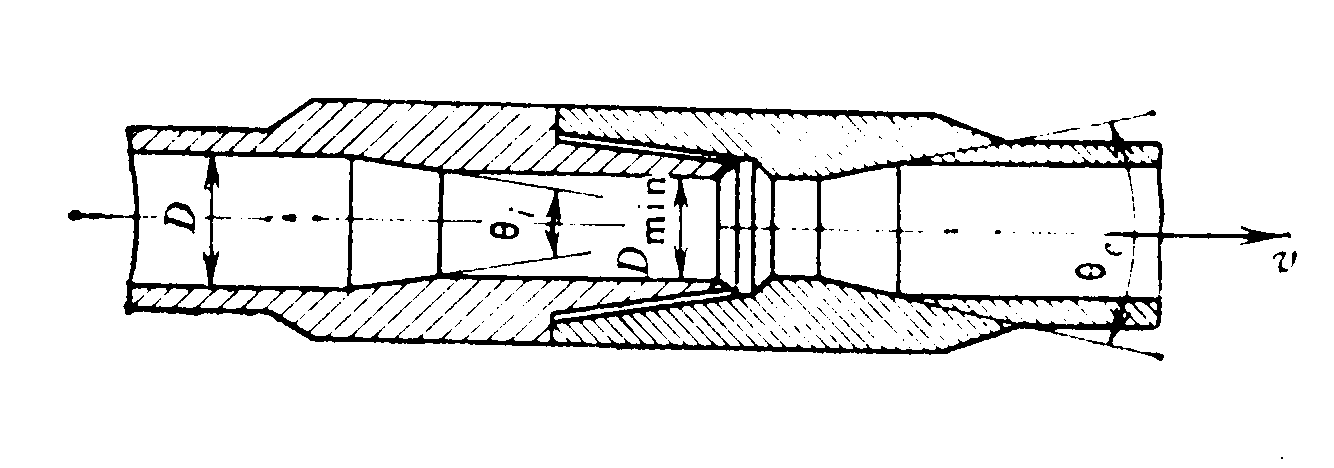



Геометрия замкового соединения бурильных труб.

с обозначениями, показанными на рисунке. Уравнение (а) пригодно при =0 45°. Поскольку угол входа потока в замковое соединение относительно мал ( =15—20°), поток сохраняет устойчивость (нет отрыва пограничного слоя и отсутствуют застойные зоны) и коэффициент пренебрежимо мал по сравнению с .

Следует особо отметить некоторые выводы, к которым пришли в результате проведенных исследований: заметное влияние угла выхода и незначительное угла входа, а также влияние критерия Re при значениях вплоть до 10000. Таким образом, при изменениях числа Re от 2000 до 20000 коэффициент уменьшается в несколько раз и только затем стабилизируется.

При отсутствии экспериментальных данных для обычных замковых соединений можно использовать формулу Борда— Карно с коэффициентом

---