Файл: Учебнометодический комплекс Для студентовбакалавров, обучающихся по направлению.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 190
Скачиваний: 3
СОДЕРЖАНИЕ
Глава 1. Понятия об основных алгебраических структурах.
§1. Алгебры. Подалгебры. Гомоморфизмы алгебр.
§3. Подгруппа. Достаточные условия подгруппы.
Глава 2. Матрицы и определители.
§1.Матрицы. Группа и кольцо матриц.
§2. Определители, их свойства.
Глава 3. Системы линейных уравнений, методы их решения.
Глава 5. Теория делимости в кольце Z.
§1. Отношение делимости в Z и его свойства.
§3. Взаимно простые числа и их свойства.
§4. НОК целых чисел и его свойства.
§5. Простые числа и их свойства.
Глава 6. Теория делимости в кольце Р[х].
§2. Отношение делимости в кольце Р[х] и его свойства.
Свойства отношения делимости в кольце Р[x].
§3. Деление с остатком в кольце P[x].
§4. Приводимые и неприводимые многочлены
Докажем единственность разложения:
Предположим, что для числа (n) есть два различных представления: n = p1p2 …pk, n = q1q2 …qn и n>k.
Тогда получим, что p1p2 …pk = q1q2 …qn (1). Левая часть равенства (1) делится на p1, тогда по свойству простых чисел (см. задача 2), по крайней мере, один из сомножителей правой части должен делиться на p1.
Пусть (q1/p1) => (q1=p1). Разделив обе части равенства (1) на p1, получим равенство p2p3 …pk = q2q3 …qn . Повторяя прежнее рассуждение ещё (k-1) раз, мы получим равенство 1 = qk+1qk+2 …qn , т.к. все qi >1, то это равенство невозможно. Следовательно, в обеих разложениях число сомножителей одинаково (k=n) и сами сомножители одинаковы.
Замечание. В разложении числа (n) на простые сомножители некоторые из них могут повторяться. Обозначая буквами 1,2,…,k кратность их вхождения в (n), получим так называемое каноническое разложение числа (n):
Пример 2.
Каноническое разложение числа 588000 = 2535372
Следствие 1. Если
Пример 3. Все делители числа 720 = 24325 получим, если в выражении
Искомые делители будут равны: 1; 2; 4; 8; 16; 3; 6; 12; 24; 48; 9; 18; 36; 72; 144; 5; 10; 20; 40; 80; 15; 30; 60; 120; 240; 45; 90; 180; 360; 720.
Следствие 2. Если
…pkk, где i = min(I, i)
[a, b] = p11 p22 …pkk , где i = max(I, i).
Пример 4. Найти НОД(a, b) и НОК(a, b), используя каноническое разложение, если
a = 24, b = 42.
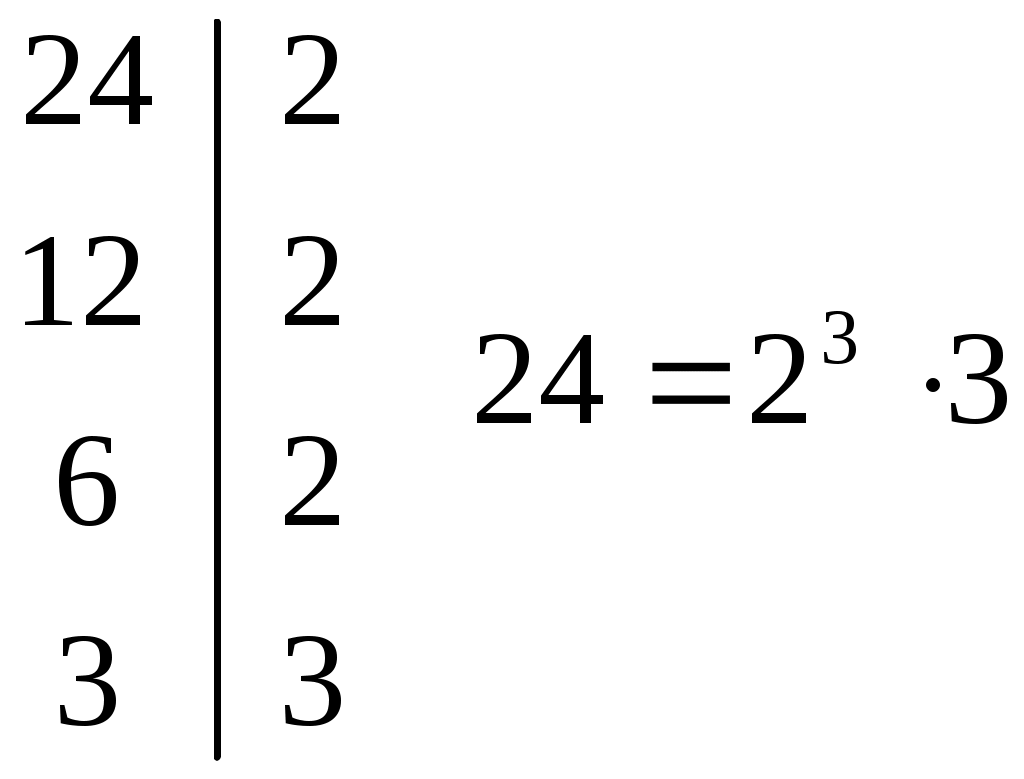
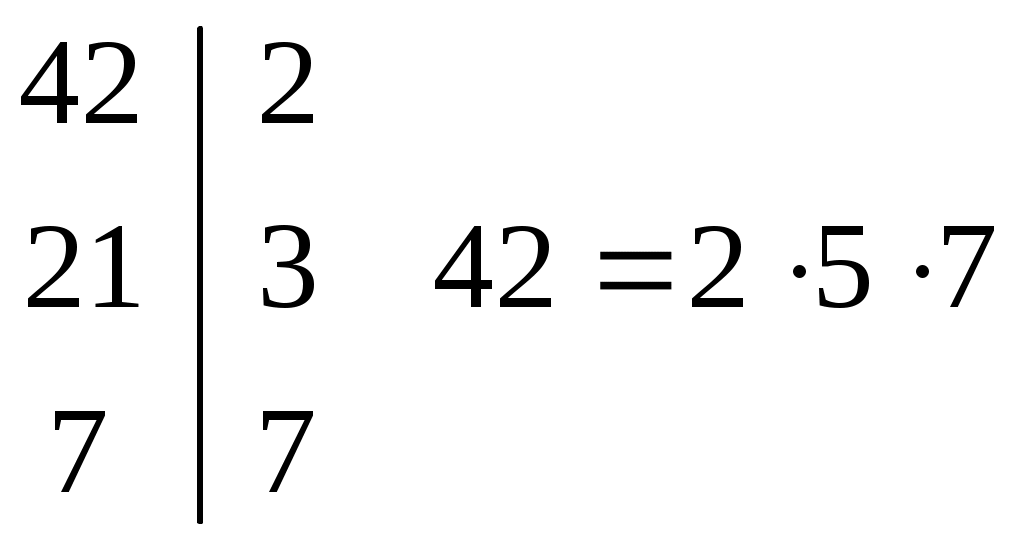
(24, 42) = 23 = 6
[24, 42] = 2337 = 168
Глава 6. Теория делимости в кольце Р[х].
В процессе изучения этой темы студенты должны овладеть следующими знаниями, умениями, навыками:
- знать определение многочлена f(x) нал полем Р;
- уметь строить кольцо многочленов <Р[х], +, •> и линейное пространство < Р[х], + {, R} >, знать его базис,
размерность и их свойства;
- знать отношение делимости в кольце Р[х];
- знать и уметь находить HOK(f, g) и НОД (f, g) различными способами;
- знать методы нахождения корней многочлена в поле R, С и Q;
- уметь разложить многочлен на неприводимые множители над полем R, С и Q;
- знать формулы Виета, «схему Горнера», уметь их использовать в процессе решения разного типа задач.
§1. Построение кольца Р[х].
Пусть дано произвольное поле Р, его элементы будем обозначать а1, а2, ..., аn...
Определение 1. Многочленом n - й степени от одной переменной называют выражение вида: аnхn + аn-1xn-1 +...+ a1x+a0, где аiР, аn 0, n N0 = N {0}.
Замечание. аiхi - называют членом многочлена; i - степенью этого члена (если аi 0); аi - коэффициентом многочлена и соответствующего члена. Если аi = 0, то члену аiхi не приписывается никакой степени, а0х0 - член нулевой степени, если а0 0 - элемент поля Р.
Для краткой записи многочленов используют знаки f(x), g(x), h(x) и т.п.
Определение 2. Многочлен f(x)= 0хn + 0хn-1 +...+ 0х + 0 называют нуль-многочленом. Его степень также не определяется.
Определение 3. Степенью многочлена f(x)называют наивысшую из степеней его членов.
Например, f(x)=x3 + 3х7 + 4х2 + 2 , cт f (x) = 7.
Из определений (1-3) следует, что всё множество многочленов Р[х] = {f(x)| f(x) = anxn+...+ ax + а0} можно разбить на три класса:
1. нуль-многочлен f(x)=0xn+... +0х+0;
2. многочлены нулевой степени (аi Î Р);
3. многочлены степени выше нулевой f(x), g(x)...
Если даны два многочлена f(x) и g(x), то всегда можно считать, что они содержат одинаковое число членов, т.к. недостающие члены всегда можно приписать с нулевыми коэффициентами, например:
f(x) = х5 - х4 + 2x3 + 3х2 - 5х + 1
g(x) = 0х5 - 0х4 + 3х3 + х2 - 0х + 5
Понятие степени позволяет задать отношение порядка на множестве многочленов P[x]:
а) либо в порядке возрастания степени их членов, например:
f(х) = 3+4х2-5х4 + х6;
б) либо в порядке убывания степени их членов, например:
f(х) = Зх5-х3 + 2х2 + 8;
Всё вышесказанное позволяет определить понятие алгебраического равенства двух многочленов.
Определение 4. f(x), g(x) Î P[x], если
f(x) = anxn+an-1 xn-1+...+ а1x+ а0 и
g(x) = bnхn+bn-1 хn-1+…+b1+b0 , то
f(x) = g(x) (аn = bn) & (an-1 = bn-1)& ... & (a0 = b0)
Это отношение будет:
а) рефлексивно, т.к. f(x), f(x)= f(x);
б) симметрично, т.к. f(x), g(x), если (f(x)= g(x)) (g(x)= f(x));
в) транзитивно, т.к. f(x), g(x), h(x), если [f(x)=g(x)]&[g(x)=h(x)] => [f(х) = h(x)]. (Проверьте!)
Таким образом, отношение равенства многочленов есть отношение эквивалентности на множестве Р[х], в каждый класс эквивалентности попадает только один многочлен.
Замечание. Выше мы определили понятие многочлена как некоторое формальное выражение, однако понятие многочлена можно определить и с других точек зрения. Например, многочлен f(x) = anxn+an-1 xn-1+...+ а1x+ а0 можно рассматривать как арифметический вектор (а0, a1, a2,...,an, 0...0), т.к. коэффициенты многочлена определяют его однозначно. Так, по вектору (3, 5, 1) можно составить многочлен f(х)= х2 + 5х + 3.
С другой стороны, многочлен f(x) можно рассматривать как некоторую функцию, определённую на множестве Р. Поэтому отношение равенства двух многочленов каждый раз определяется по-новому (как равенство двух арифметических векторов и как равенство двух функций).
Определим на множестве Р[х] три операции:
1. f, g P[x], f + g = (an + bn)xn + (an-1 + bn-1)xn-1 + ...+ (a0 + b0)
2. f P[x] , P, f=anxn +an-1xn-1+…+a1x +a0
3. f, gP[x], fg = a0b0 + (a0b1 + a1b0)x+…+(a0bi
+...+ aibi-1 + aib0)xi + +... + anbmxn+m
Замечание. Из этих определений следует, что действия сложения и умножения - это бинарные операции, действие умножения на скаляр при фиксированном , будет унарной операцией.
Пример 1. Пусть f(x) = 3х5 - 2х3 + 4, g(x) = 2х4 + х2 + 1, тогда
f(x) + g(x) = 3х5 + 2х4 + 2х3 + х2 + 5
f(x) • g(x) = (3х5 + 2х3 + 4)(2х4 + х2 + 1) = 6х9 + 3х7 + 3х5 + 4х7 + 2х5 + 2х3 + 8х4 + 4x2 + 4 = 6х9 + 7х7 + 5х5 + 8х4 + 2x3 + 4х2 + 4
3 • g(x) = 6х4 + Зх2 + 3
Свойства степени многочлена вытекают из определения операций:
1. свойство Если f(x) 0 и g(x) 0, то
cm(f(x) + g(x)) max(cm f(x), cm g(x))
2. свойство Если f(x) 0 и g(x) 0,то cm (f(x)g(x)) = cm f(x) + cm g(x)
Действительно, это следует из определения операции умножения и того, что если cm f(x) = n, значит аn 0, если cm g(x) = m, значит bm 0, тогда аnbm 0 т.к. аn ,bm P, а в поле делителей нуля нет. Поэтому член аnbmxm+n многочлена f(x)g(x) будет иметь наивысшую степень (m+n).
Это свойство позволяет сделать вывод, о том, что множество многочленов не содержит делителей нуля.
Теорема 1. Алгебра <Р[х], +, •> - является коммутативным, ассоциативным кольцом с единицей.
Доказательство.
I. Нужно проверить, что множество Р[х] - множество многочленов, замкнуто относительно указанных операций
II. Проверить выполнение следующих аксиом:
1. f, g P[x], f + g = g + f
2. f, g, h P[x], (f + g) + h = f + (g + h)
3. 0 Î P[x]: " f Î P[x], 0 + f = f + 0 = f
4. f P[x] (-f) P[x]: f + (-f) = (-f) + f = 0
5. f, g, h P[x], (f + g)h = fh + gh, h(f + g) = hf + hg
6. f, g P[x], f g = g f
7. f, g, h P[x], (f g) h = f (g h)
8. " f Î P[x], l f = f
Проверить каждую аксиому самостоятельно.