Файл: Задача 1 Расчет нелинейной электрической цепи переменного тока.docx
Добавлен: 26.10.2023
Просмотров: 32
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
. Институт химии и энергетики .
. Кафедра «Электроснабжение и электротехника» .
Расчетно-графическая работа №2
Задание №1
по учебному курсу «Теоретические основы электротехники – 2»
Вариант 4.13
Обучающегося:
Группа:
Преподаватель: Шлыков С.В.
Тольятти 2023
Задача №1 «Расчет нелинейной электрической цепи переменного тока»
В заданной, согласно варианту, расчетной электрической цепи необходимо:
1. Произвольно задайтесь максимальным значением входного напряжения
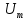 . Изобразите временные диаграммы на интервале двух периодов входного
. Изобразите временные диаграммы на интервале двух периодов входного 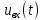 и выходного
и выходного 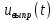 напряжений полупроводникового выпрямителя согласно варианту (пакет Mathcad), считая полупроводниковый диод идеальным (рисунок 1).
напряжений полупроводникового выпрямителя согласно варианту (пакет Mathcad), считая полупроводниковый диод идеальным (рисунок 1).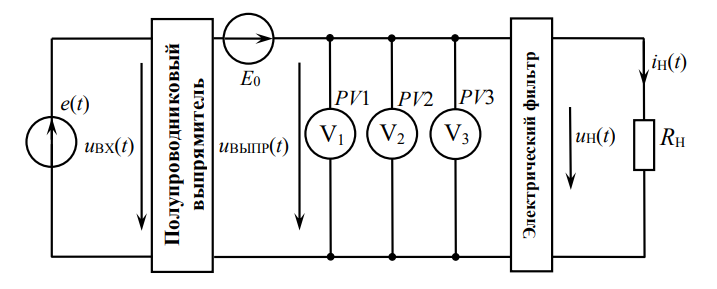
Рисунок 1 – Расчетная электрическая цепь.
2. Разложите в ряд Фурье кривую выходного напряжения полупроводникового выпрямителя
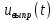 , ограничившись пятью ненулевыми гармоническими составляющими ряда. Запишите получившееся выражение несинусоидальной функции напряжения
, ограничившись пятью ненулевыми гармоническими составляющими ряда. Запишите получившееся выражение несинусоидальной функции напряжения 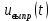 и постройте данную кривую напряжения на интервале двух периодов. Постройте спектр амплитуд и фаз полученного сигнала;
и постройте данную кривую напряжения на интервале двух периодов. Постройте спектр амплитуд и фаз полученного сигнала;3. Определите показания приборов различных систем измерения:
Вольтметр PV1 – прибор магнитоэлектрической системы;
Вольтметр PV2 – прибор электромагнитной системы;
Вольтметр PV3 – прибор выпрямительной системы;
Показания приборов занести в таблицу.
Приведите вычисления каждого значения напряжения вольтметров.11 Найдите коэффициент искажения несинусоидальной функции напряжения полупроводникового выпрямителя
 .
.4. Рассчитайте напряжение
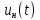 , от каждой составляющей ряда Фурье, в нагрузочном резисторе, считая, что в качестве фильтра используется L-фильтр. Запишите полученное выражение
, от каждой составляющей ряда Фурье, в нагрузочном резисторе, считая, что в качестве фильтра используется L-фильтр. Запишите полученное выражение 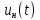 . Постройте кривую напряжения
. Постройте кривую напряжения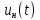 и сравните с кривой напряжения пункта 2. Постройте спектр амплитуд и фаз полученного сигнала. Определите коэффициент искажения несинусоидальной функции напряжения
и сравните с кривой напряжения пункта 2. Постройте спектр амплитуд и фаз полученного сигнала. Определите коэффициент искажения несинусоидальной функции напряжения 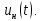
5. Рассчитайте напряжение
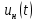 , от каждой составляющей ряда Фурье, в нагрузочном резисторе, считая, что в качестве фильтра используется С-фильтр. Запишите полученное выражение
, от каждой составляющей ряда Фурье, в нагрузочном резисторе, считая, что в качестве фильтра используется С-фильтр. Запишите полученное выражение 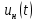 . Постройте кривую напряжения
. Постройте кривую напряжения 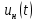 и сравните с кривой напряжения пункта 2. Постройте спектр амплитуд и фаз полученного сигнала. Определите коэффициент искажения несинусоидальной функции напряжения
и сравните с кривой напряжения пункта 2. Постройте спектр амплитуд и фаз полученного сигнала. Определите коэффициент искажения несинусоидальной функции напряжения 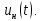
6. Изобразите схему заграждающего (полосового) L-C-фильтра, который необходимо включить для подавления (пропускания) одной частоты гармоники, заданной вариантом. Рассчитайте параметры L-C фильтра. Рассчитайте напряжение
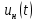 , от каждой составляющей ряда Фурье, в нагрузочном резисторе и построить кривую напряжения
, от каждой составляющей ряда Фурье, в нагрузочном резисторе и построить кривую напряжения 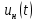 . Определите коэффициент искажения несинусоидальной функции напряжения
. Определите коэффициент искажения несинусоидальной функции напряжения 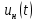 .
.Закон изменения входного напряжения:
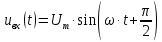 .
.Таблица 1 – Значения варианта.
| E0 | 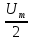 |
| Номер гармоники | 0 |
| Тип фильтра | ПФ |
ПФ – полосовой фильтр. Однополупериодный выпрямитель.
Пункт 1
Зададимся произвольным максимальным значением входного напряжения Um. Пусть это максимальное значение входного напряжения равно: Um=550 В.
Изобразим временные диаграммы входного и выходного напряжений полупроводникового выпрямители в математическом пакете Mathcad. Для этого необходимо аналитически представить выражения соответствующих мгновенных напряжений.
Выражение входного напряжения
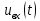 запишется следующим образом (формула 1):
запишется следующим образом (формула 1):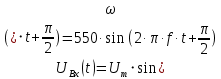 (1)
(1)Полупроводниковый выпрямитель является однополупериодным, следовательно, его схема состоит из одного полупроводникового диода VD и резистора R (рисунок 2). Напряжение на выходе выпрямителя будет наблюдаться только при положительной полуволне источника питания e(t). Источник постоянной ЭДС E0 создает смещение по оси напряжения равное (формула 2):
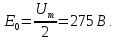 (2)
(2)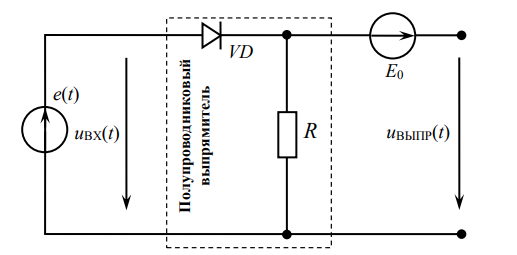
Рисунок 2 – Расчетная электрическая цепь в пункте 1
Таким образом, функция выходного напряжения выпрямителя является кусочно-заданной на интервале одного периода и запишется она следующим образом (формула 3).
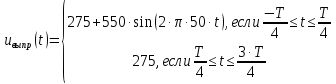 (3)
(3)Воспользуемся встроенной панелью инструментов «График» в математическом пакете Mathcad и построим два графика входного и выходного напряжений полупроводникового выпрямителя на интервале двух периодов (рис. 3).
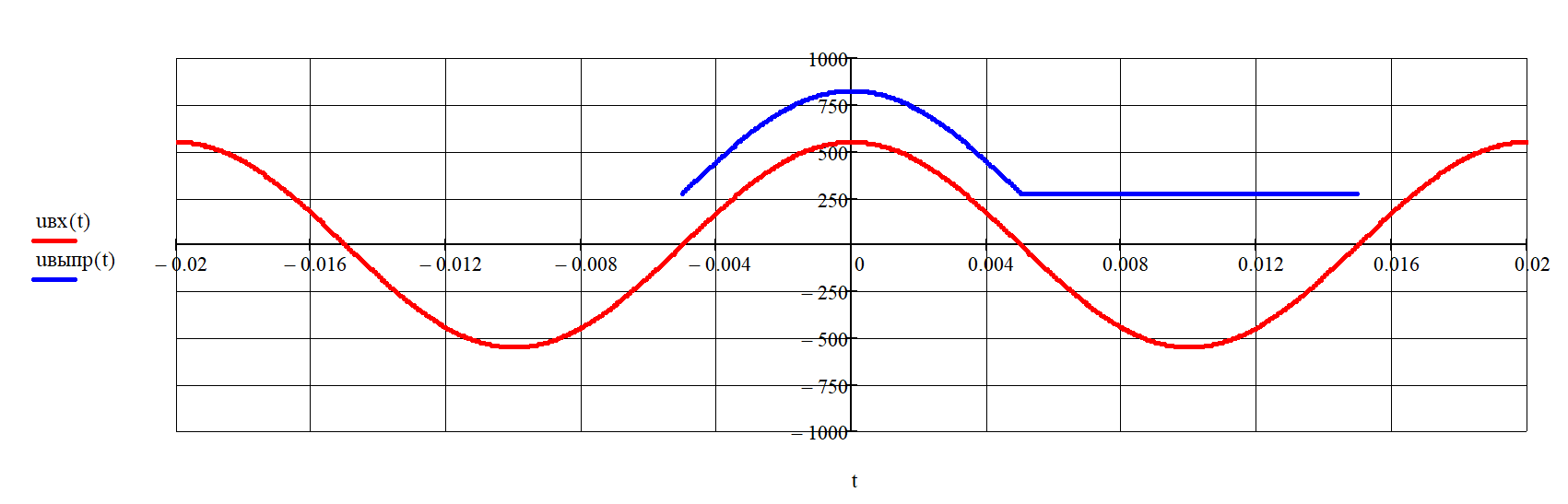
Рисунок 3 – Временные диаграммы напряжений полупроводникового выпрямителя
Временная диаграмма входного напряжения полупроводникового выпрямителя uвх(t) показана красным цветом, а выходного uвыпр(t) - синим цветом. Видно, что временные зависимости напряжений соответствуют алгоритму работы однополупериодного выпрямителя.
Пункт 2
Для дальнейшего расчета электрической цепи разложим кривую выходного напряжения полупроводникового выпрямителя uвыпр(t) в ряд Фурье. Данная кривая представляет собой периодическую негармоническую функцию напряжения, которая может быть разложена в тригонометрический ряд Фурье (формула 4).
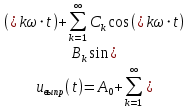 (4)
(4)где k – порядковый номер гармоники, А0 – нулевая гармоника или постоянная составляющая, Bk – амплитуды синусных гармоник, Сk – амплитуды косинусных гармоник.
Найдем величину постоянной составляющей ряда Фурье по формуле 5.
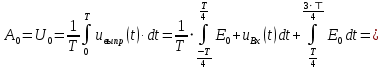
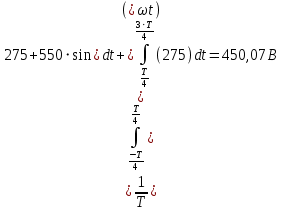 (5)
(5)Пределы интегрирования и сама подынтегральная функция определяются по ранее записанной формуле 3.
Амплитуды синусных гармоник ряда Фурье находим по формуле 6.
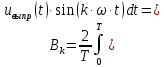
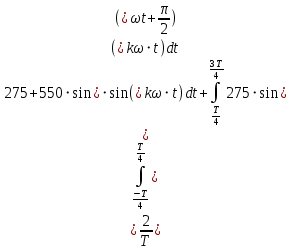 (6)
(6)Амплитуды косинусных гармоник ряда Фурье находим по формуле 7.
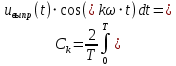
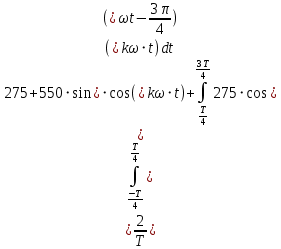 (7)
(7)Расчет амплитуд синусных и косинусных гармонических составляющих ряда Фурье был произведен в математическом пакете Mathсad и результат этого расчета сведен в таблицу 2.
Поскольку тригонометрические функции синус и косинус образуют квадратуру, то каждую гармоническую составляющую можно представить в виде тригонометрической функции синуса, которая имеет начальную фазу. В этом случае, ряд Фурье приводится в так называемую амплитудно-фазовую форму (формула 8).
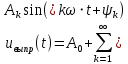 (8)
(8)где Аk – амплитуды синусных гармоник, начальные фазы которых равны ψk. Параметры синусоидальных гармонических составляющих определяются по формуле 9.
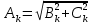
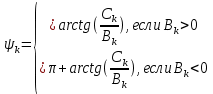 (9)
(9)Результаты вычислений в математическом пакете Mathсad сведём в таблицу 2.
Таблица 2 – Параметры гармоник ряда Фурье.
| K, номер гармоники | Амплитуды гармоник, В | Начальные фазы гармоник | |||
| Bk | Ck | Ak | 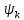 ,рад ,рад | 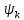 ,° ,° | |
| 1 | 0 | 275 | 275 | 1,571 | 90 |
| 2 | -0 | 116,714 | 116,71 | 1,571 | 90 |
| 3 | 0 | 0 | 0 | 1,43 | 81,931 |
| 4 | 0 | -23,343 | 23,34 | 4,712 | 270 |
| 5 | -0 | 0 | 0 | 2,662 | 152,54 |
| 6 | 0 | 10,004 | 10 | 1,571 | 90 |
| 7 | 0 | -0 | 0 | -0,432 | -24,746 |
| 8 | -0 | -5,558 | 5,56 | 4,712 | 270 |
| 9 | 0 | 0 | 0 | 1,168 | 66,946 |
| 10 | -0 | 3,537 | 3,54 | 1,571 | 90 |
Окончательно запишем получившееся выражение несинусоидальной функции выходного напряжения полупроводникового выпрямителя uвыпр(t). Данное выражение представлено рядом Фурье, в котором число ненулевых гармонических составляющих ограничено пятью членами (формула 10).
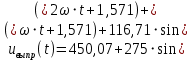
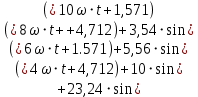 (10)
(10)Воспользуемся встроенной панелью инструментов «График» в математическом пакете Mathcad и построим кривую выходного напряжения полупроводникового выпрямителя uвыпр(t) на интервале двух периодов (рисунок 5). Видно, что форма кривой напряжения, представленная тригонометрическим рядом Фурье, достаточно точно описывает выходное напряжение полупроводникового выпрямителя uвыпр(t). Для этого достаточно пяти гармонических составляющих ряда Фурье.
Гармонический состав функции выходного напряжения полупроводникового выпрямителя uвыпр(t) можно задать при помощи дискретных спектров амплитуд и фаз. В математическом пакете Mathcad создадим два массива амплитуд и начальных фаз гармонических составляющих ряда Фурье.
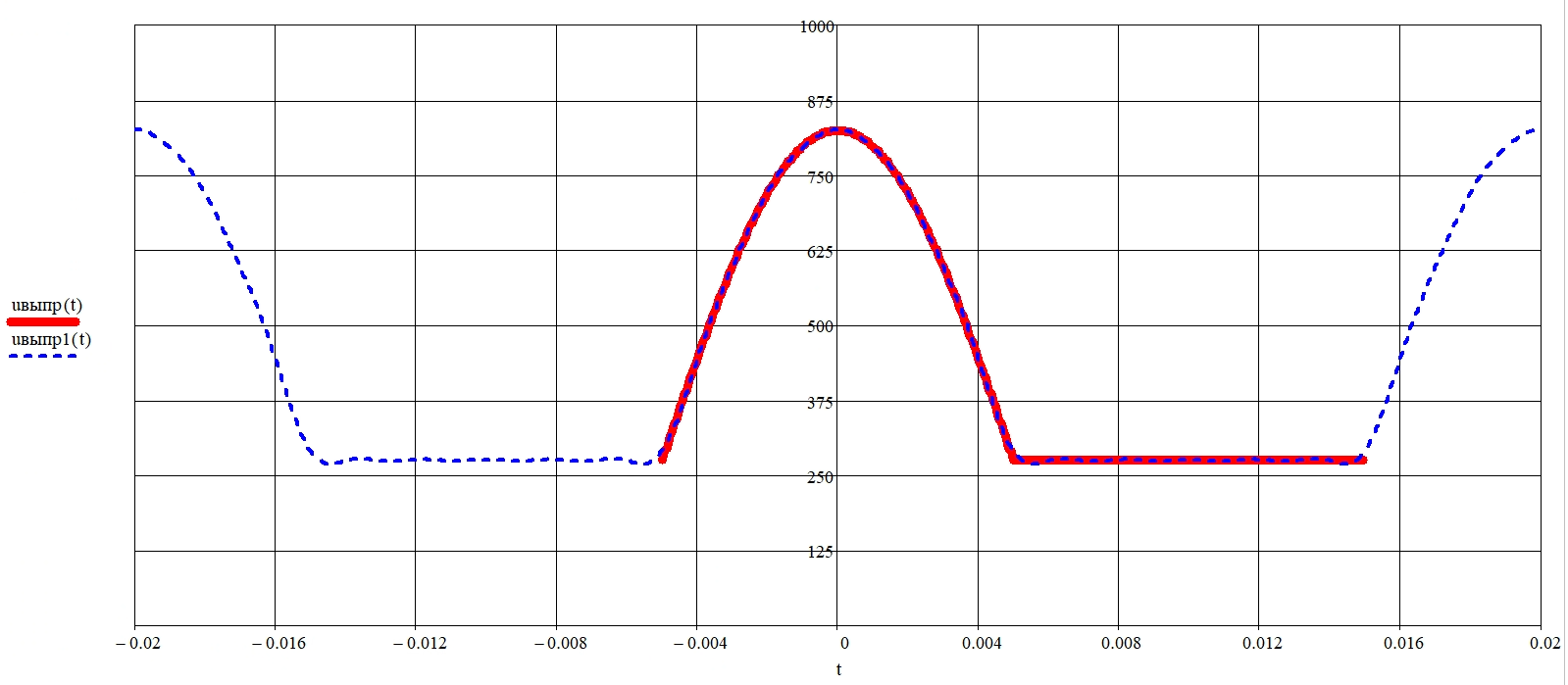
Рисунок 4 – Форма кривой выходного напряжения полупроводникового выпрямителя uвыпр(t)
С помощью встроенной панели инструментов «График» отобразим амплитуды гармонических составляющих ряда Фурье в зависимости от номера гармоники и получим график спектра амплитуд (рисунок 4) выходного напряжения выпрямителя.
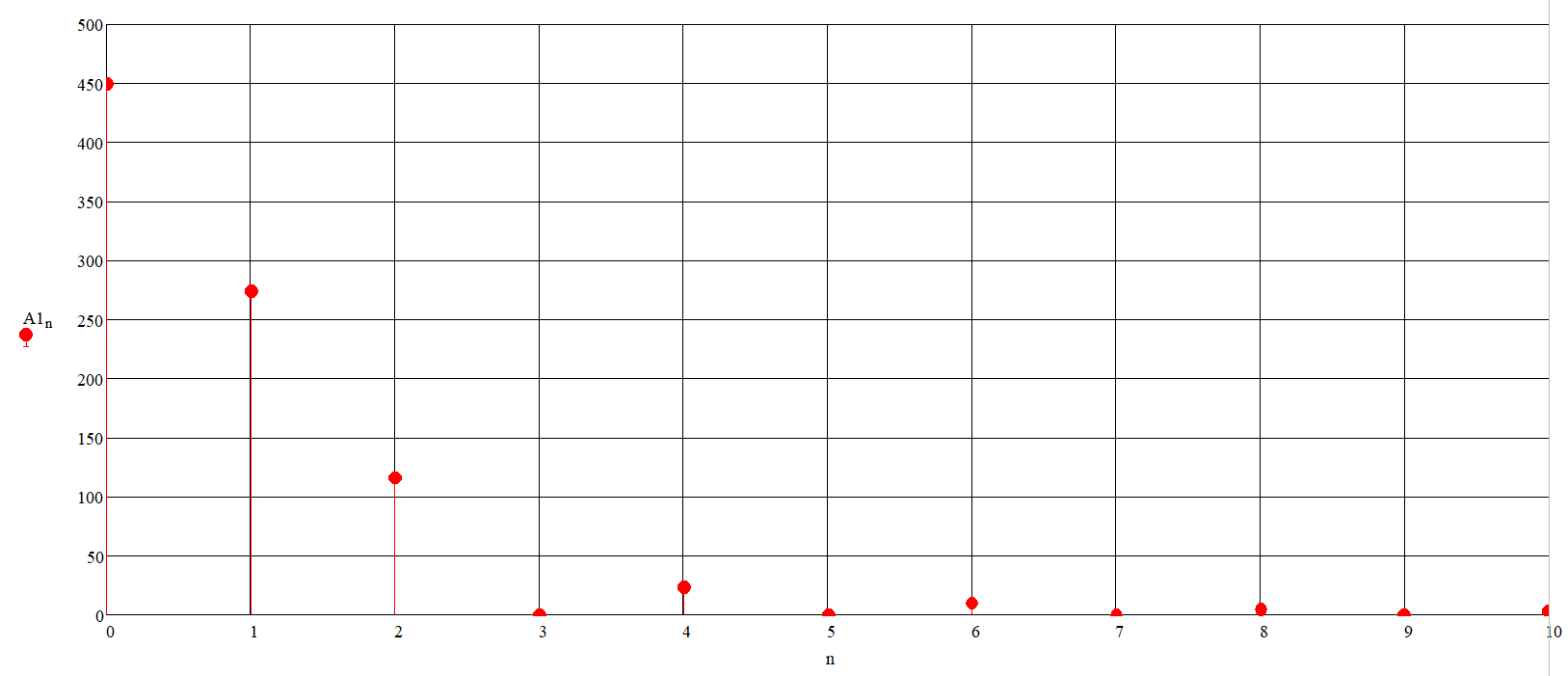
Рисунок 5 – Дискретный спектр амплитуд
Значения начальных фаз гармонических составляющих ряда Фурье отобразим в градусах и получим график спектра фаз (рисунок 5) выходного напряжения выпрямителя.
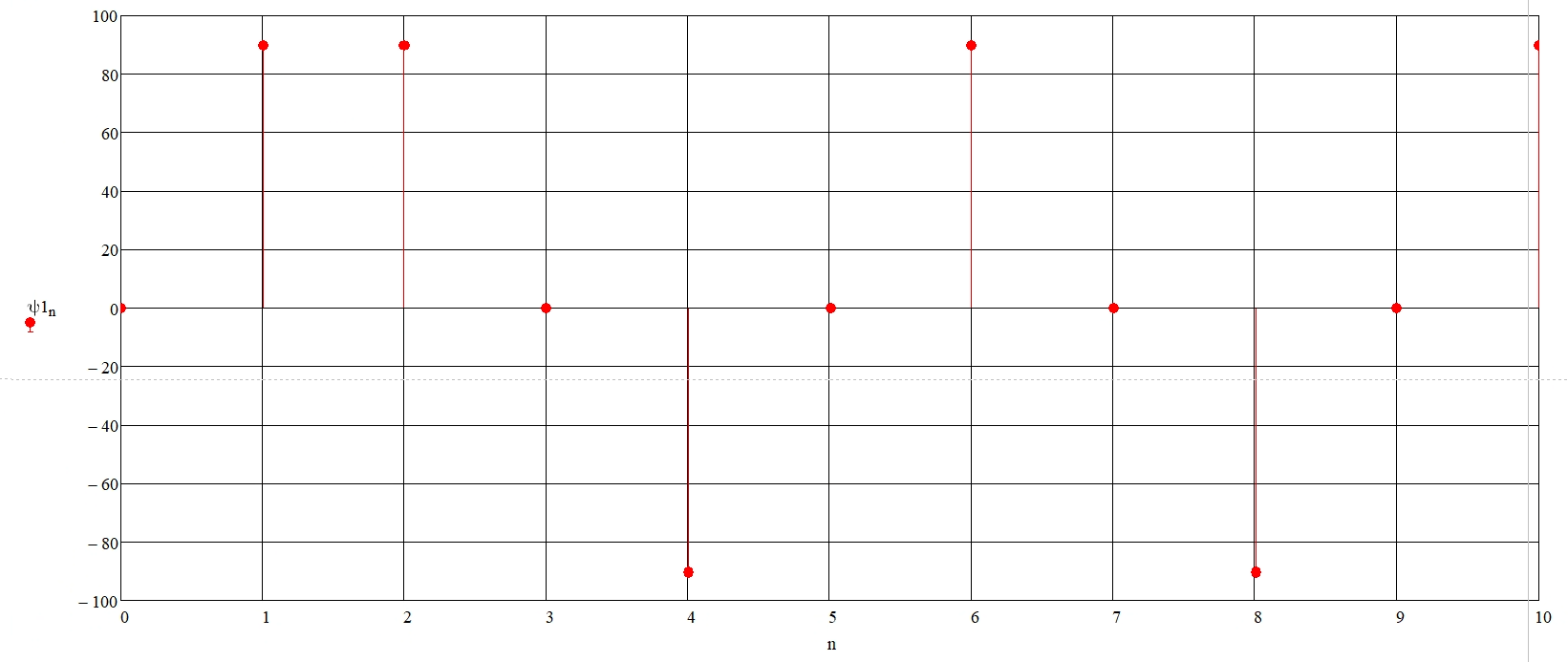
Рисунок 6 – Дискретный спектр фаз
Проведя анализ графика спектра амплитуд, можно сделать вывод, что амплитуды высших гармоник резко убывают.
Пункт 3
Определим показания вольтметров различных систем измерения (рис. 7).
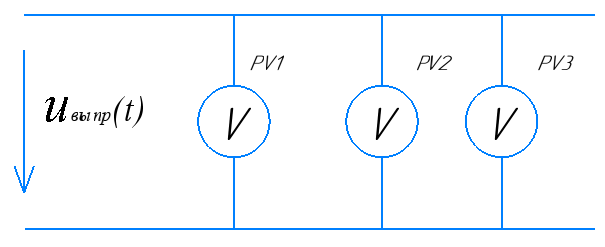
Рисунок 7 – Расчетная электрическая цепь в пункте 3
Вольтметр PV1 является измерительным прибором магнитоэлектрической системы, который реагирует на постоянную составляющую ряда Фурье, представленного в формуле 10. Расчет данного значения показано в формуле 11.